Upper Bound
Binary Search
Fundamentals
Easy
- The underlying concept of the 'upper bound' problem is used in database indexing strategies
- When querying data, databases often need to quickly find the range of entries that satisfy a certain condition
- For instance, finding all customers whose yearly income is above a certain value
- Here, the 'upper bound' function can efficiently return the first record that exceeds the specified income, and all successive records can be retrieved from there
- This allows significant speedup in the processing of such queries, ultimately enhancing performance of applications that rely on large databases
Given a sorted array of nums and an integer x, write a program to find the upper bound of x. The upper bound algorithm finds the first or the smallest index in a sorted array where the value at that index is greater than a given key i.e. x.
If no such index is found, return the size of the array.
Examples:
Input : n= 4, nums = [1,2,2,3], x = 2
Output:3
Explanation: Index 3 is the smallest index such that arr[3] > x.
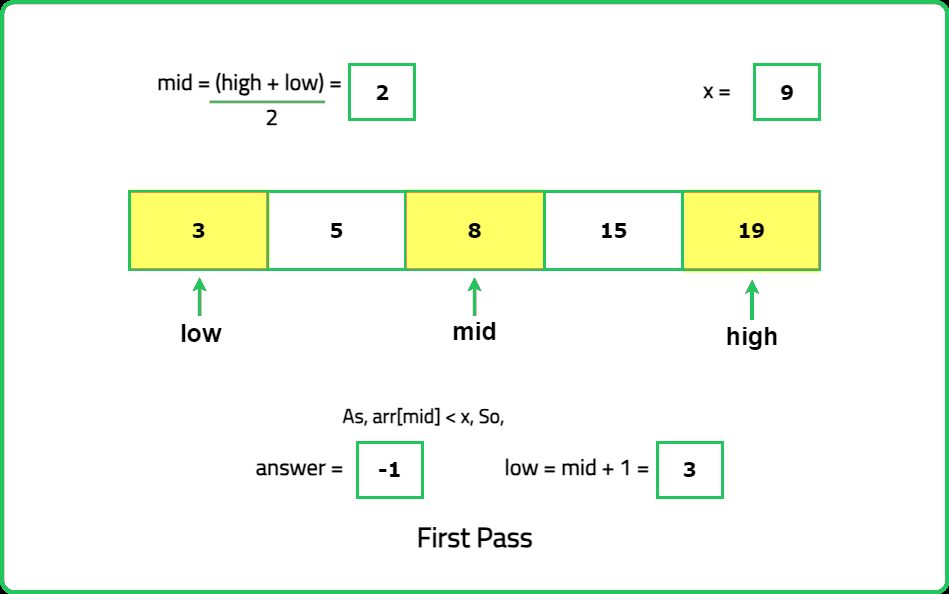
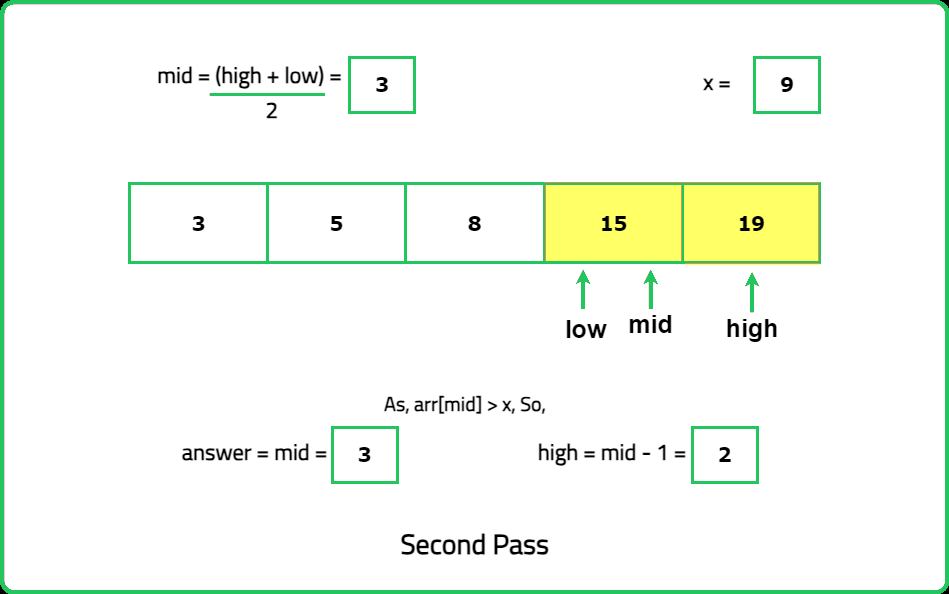
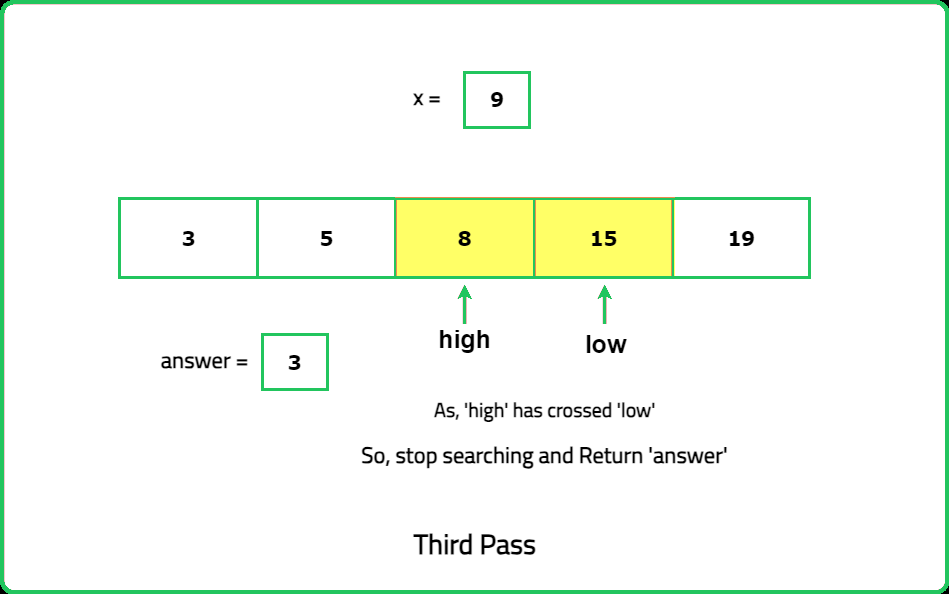
Input : n = 5, nums = [3,5,8,15,19], x = 9
Output: 3
Explanation: Index 3 is the smallest index such that arr[3] > x.
Input : n = 5, nums = [3,5,8,15,19], x = 3
Constraints
- 1 <= nums.length <= 105
- -105 < nums[i], x < 105
- nums is sorted in ascending order.
Hints
- "The upper bound doesn’t care about whether x exists in the array. It’s about finding the smallest index where nums[index]>x."
- "Use the usual binary search setup, but adjust the condition: If nums[mid]>x, the result could be at mid, so move the high pointer to search the left half. Otherwise, move the low pointer to search the right half. Stop when the low pointer overtakes the high pointer."
Company Tags
American Express
Shopify
Stripe
Micron Technology
Intel
Siemens Healthineers
Square
Bloomberg
Western Digital
Teladoc Health
Docker
Airbnb
Red Hat
Roblox
Target
Swiggy
Deloitte
Broadcom
HashiCorp
Pinterest
Optum
NVIDIA
Zomato
Splunk
Activision Blizzard
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro