Palindrome partitioning II
Dynamic Programming
MCM DP
Hard
Given a string s, partition s such that every substring of the partition is a palindrome.Return the minimum cuts needed for a palindrome partitioning of s.
Examples:
Input : s = "aab"
Output : 1
Explanation : The palindrome partitioning ["aa", "b"] could be produced using 1 cut.
Input : s = "abaaba"
Output : 0
Explanation : The complete string can be considered as a partition as the string itself is palindrome.
There are other ways to partition the string but it requires more number of cuts.
Input : s = "abcd"
Constraints
- 1 <= s.length <= 2000
- s consist of only lowercase English letters
Hints
- Define dp[i] as the minimum number of cuts needed to partition s[0:i] into palindromes. Check all possible palindrome substrings ending at i.
- "Define isPalindrome[i][j] = True if s[i:j] is a palindrome. Use isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]) for efficient checking."
Company Tags
Teladoc Health
Philips Healthcare
Pinterest
Square
Medtronic
Unity Technologies
Visa
Cerner
AMD
Electronic Arts
Uber
Wayfair
Stripe
Epic Systems
Swiggy
Oracle
Western Digital
Boston Consulting Group
Micron Technology
Johnson & Johnson
Texas Instruments
IBM
Ernst & Young
Shopify
Bain & Company
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Understanding:
In order to solve this problem, we need to partition the given string in such a way that every substring of the partition becomes a palindrome. For example, if the string “aabb” is given, one of the valid partitions will be “aa | b | b”.
Now, one key point to notice here is that we can make every substring of any string a palindrome, by partitioning it n-1 times(where n = size of the string). For example, if the given string is “abcd” and if we partition it n-1 i.e. (4-1 = 3) times, it will be like, a | b | c | d. Here, every single substring of the partitions is a palindrome.
So, we can conclude that it is very much possible all the time to partition a string in such a way that every substring becomes a palindrome and we can also assure that the answer always exists. Here, in this question, it is clearly mentioned that we need to figure out the minimum number of such partitions. Consider the example given below:
Intuition:
This type of problem is generally solved using the front partition. Following the front partition technique, we will start checking from the first index of the given string and will check if we can make a partition between the first and the second index. Similarly, then we will include the second index in the account and check if we can make a partition between the second and the third index. This process will continue to the last index. The condition for a partition to be valid is that the left part of the partition must be a palindromic substring.
Rules to solve this problem:
- Express the given string in terms of the index: We are given a string. Now, following the front partition rules we will place i to index 0 i.e. the first index.
- Try out all partitions: As we have figured out the logic for marking the pointer, i, we will move to the partitioning loop. We can simply write a for loop(say j) starting from i to n-1(n = size of the string), The problem is being broken in the following manner:
- Base case: When the index i will be equal to the size of the string(i.e. i == n), we can say there are no more characters left to be partitioned. So, this is the base case and in this case, the function will return 0.
- Return the best possible answer of all partitions: A partition is possible when the left substring of that partition is a palindrome. Now, inside the partitioning loop, we will check if the partition can be done at index j(i.e. We will check if the substring starts from index i and ends at index j is a palindrome or not). If it is done, we will add 1 to our answer, and then we will again follow the same method for the left-over substring.
123456789
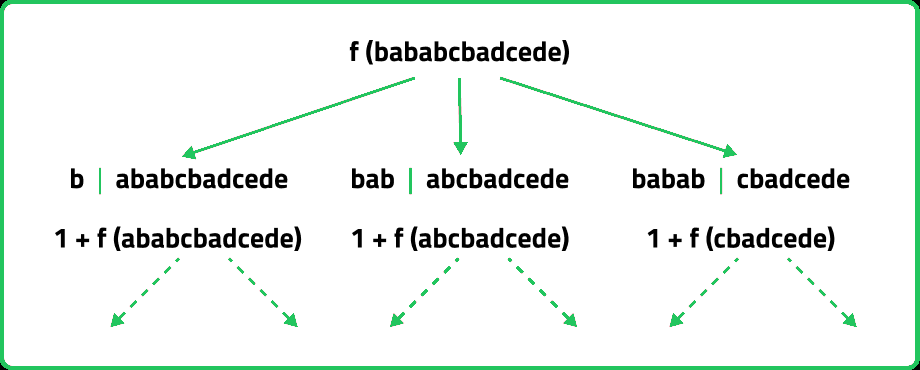
/*It is a pseudocode and it not tied to
any specific programming language*/
f(i){
//Partition loop
for(int j = i; j < n; j++){
//Calculation
}
}Here, in the question, it is clearly mentioned that we need the minimum number of partitions. So, calculating all possible answers using the above method, we will take the minimum into our consideration.
12345678910111213
/*It is a pseudocode and it not tied to
any specific programming language*/
f(i){
//Partition loop
for(int j = i; j < n; j++){
if(isPalindrome(s, i, j)){
int cost = 1 + f(j+1, s)
minCost = min(minCost, cost)
}
}
return minCost
}Note about the final answer:
If we carefully observe, we can notice that our function is actually counting an extra partition at the end of the string in each case. For example, the given string is “abcd”. After doing a partition after ‘c’ the function will check if a partition can be done after ‘d’ to check if the last substring i.e. ‘d’ itself is a palindrome. Consider the following illustration: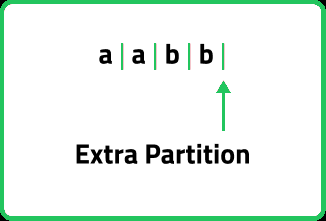
For that our function will return 4 as the answer, instead of the actual answer is 3. So, our actual answer will be (number of partitions returned by the function - 1).
Steps for recursive approach:
- Convert the problem to a recursive function marked by the pointer i.
- Use a loop to check all possible partitions of the string and calculate the number of partitions.
- Return the minimum number of partitions counted.
- Base case: When the index i will be equal to the size of the string(i.e. i == n), we can say there are no more characters left to be partitioned. So, this is the base case and in this case, the function will return 0.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
// Function to check if substring is a palindrome.
bool isPalindrome(int i, int j, string &s) {
while (i < j) {
if (s[i] != s[j]) return false;
i++;
j--;
}
return true;
}
/* Recursive function to find the minimum
number of partitions to make palindromes.*/
int minPartitions(int i, int n, string &str) {
// Base case: If we've reached the end of string.
if (i == n) return 0;
int minCost = INT_MAX;
/* Consider all possible substrings
starting from the current index.*/
for (int j = i; j < n; j++) {
if (isPalindrome(i, j, str)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
int cost = 1 + minPartitions(j + 1, n, str);
minCost = min(minCost, cost);
}
}
//Return the result
return minCost;
}
public:
/* Main function to find the minimum number
of partitions for palindrome partitioning.*/
int minCut(string s) {
int n = s.size();
/* Calling recursive function and subtracting
1 as it counts partitions, not cuts.*/
return minPartitions(0, n, s) - 1;
}
};
int main() {
string str = "BABABCBADCEDE";
//Create an instance of Solution class
Solution sol;
cout << "The minimum number of partitions: " << sol.minCut(str) << "\n";
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
import java.util.*;
class Solution {
// Function to check if substring is a palindrome.
private boolean isPalindrome(int i, int j, String s) {
while (i < j) {
if (s.charAt(i) != s.charAt(j)) return false;
i++;
j--;
}
return true;
}
/* Recursive function to find the minimum
number of partitions to make palindromes.*/
private int minPartitions(int i, int n, String str) {
// Base case: If we've reached the end of string.
if (i == n) return 0;
int minCost = Integer.MAX_VALUE;
/* Consider all possible substrings
starting from the current index.*/
for (int j = i; j < n; j++) {
if (isPalindrome(i, j, str)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
int cost = 1 + minPartitions(j + 1, n, str);
minCost = Math.min(minCost, cost);
}
}
// Return the result
return minCost;
}
/* Main function to find the minimum number
of partitions for palindrome partitioning.*/
public int minCut(String s) {
int n = s.length();
/* Calling recursive function and subtracting
1 as it counts partitions, not cuts.*/
return minPartitions(0, n, s) - 1;
}
public static void main(String[] args) {
String str = "BABABCBADCEDE";
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("The minimum number of partitions: " + sol.minCut(str));
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
class Solution:
# Function to check if substring is a palindrome.
def isPalindrome(self, i, j, s):
while i < j:
if s[i] != s[j]:
return False
i += 1
j -= 1
return True
""" Recursive function to find the minimum
number of partitions to make palindromes."""
def minPartitions(self, i, n, s):
# Base case: If we've reached the end of string.
if i == n:
return 0
minCost = float('inf')
""" Consider all possible substrings
starting from the current index."""
for j in range(i, n):
if self.isPalindrome(i, j, s):
""" If the substring is a palindrome,
calculate the cost and minimize it."""
cost = 1 + self.minPartitions(j + 1, n, s)
minCost = min(minCost, cost)
# Return the result
return minCost
""" Main function to find the minimum number
of partitions for palindrome partitioning."""
def minCut(self, s):
n = len(s)
""" Calling recursive function and subtracting
1 as it counts partitions, not cuts."""
return self.minPartitions(0, n, s) - 1
if __name__ == "__main__":
str = "BABABCBADCEDE"
# Create an instance of Solution class
sol = Solution()
# Print the result
print("The minimum number of partitions:", sol.minCut(str))
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
class Solution {
// Function to check if substring is a palindrome.
isPalindrome(i, j, s) {
while (i < j) {
if (s[i] !== s[j]) return false;
i++;
j--;
}
return true;
}
/* Recursive function to find the minimum
number of partitions to make palindromes.*/
minPartitions(i, n, str) {
// Base case: If we've reached the end of string.
if (i === n) return 0;
let minCost = Number.MAX_VALUE;
/* Consider all possible substrings
starting from the current index.*/
for (let j = i; j < n; j++) {
if (this.isPalindrome(i, j, str)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
let cost = 1 + this.minPartitions(j + 1, n, str);
minCost = Math.min(minCost, cost);
}
}
// Return the result
return minCost;
}
/* Main function to find the minimum number
of partitions for palindrome partitioning.*/
minCut(s) {
let n = s.length;
/* Calling recursive function and subtracting
1 as it counts partitions, not cuts.*/
return this.minPartitions(0, n, s) - 1;
}
}
const str = "BABABCBADCEDE";
// Create an instance of Solution class
const sol = new Solution();
// Print the result
console.log("The minimum number of partitions:", sol.minCut(str));
Complexity Analysis:
Time Complexity: Exponential.Space Complexity: O(N), As we are using auxiliary stack space.
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
In order to convert a recursive solution to memoization the following steps will be taken:- Declare a dp array of size [n]: As there is only one changing parameters in the recursive solution, 'i'. The value of 'i' ranges from 0 to n-1. Therefore, we need 1D dp array.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
// Function to check if substring is a palindrome.
bool isPalindrome(int i, int j, string &s) {
while (i < j) {
if (s[i] != s[j]) return false;
i++;
j--;
}
return true;
}
/* Recursive function to find the minimum
number of partitions to make palindromes.*/
int minPartitions(int i, int n, string &str, vector<int> &dp) {
// Base case: If we've reached the end of string.
if (i == n) return 0;
//Check if the subproblem is already solved
if (dp[i] != -1) return dp[i];
int minCost = INT_MAX;
/* Consider all possible substrings
starting from the current index.*/
for (int j = i; j < n; j++) {
if (isPalindrome(i, j, str)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
int cost = 1 + minPartitions(j + 1, n, str, dp);
minCost = min(minCost, cost);
}
}
//Return the result
return dp[i] = minCost;
}
public:
/* Main function to find the minimum number
of partitions for palindrome partitioning.*/
int minCut(string s) {
int n = s.size();
vector<int> dp(n, -1);
/* Calling recursive function and subtracting
1 as it counts partitions, not cuts.*/
return minPartitions(0, n, s, dp) - 1;
}
};
int main() {
string str = "BABABCBADCEDE";
//Create an instance of Solution class
Solution sol;
cout << "The minimum number of partitions: " << sol.minCut(str) << "\n";
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
import java.util.*;
class Solution {
// Function to check if substring is a palindrome.
private boolean isPalindrome(int i, int j, String s) {
while (i < j) {
if (s.charAt(i) != s.charAt(j)) return false;
i++;
j--;
}
return true;
}
/* Recursive function to find the minimum
number of partitions to make palindromes.*/
private int minPartitions(int i, int n, String str, int[] dp) {
// Base case: If we've reached the end of string.
if (i == n) return 0;
// Check if the subproblem is already solved
if (dp[i] != -1) return dp[i];
int minCost = Integer.MAX_VALUE;
/* Consider all possible substrings
starting from the current index.*/
for (int j = i; j < n; j++) {
if (isPalindrome(i, j, str)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
int cost = 1 + minPartitions(j + 1, n, str, dp);
minCost = Math.min(minCost, cost);
}
}
// Return the result
return dp[i] = minCost;
}
/* Main function to find the minimum number
of partitions for palindrome partitioning.*/
public int minCut(String s) {
int n = s.length();
int[] dp = new int[n];
Arrays.fill(dp, -1);
/* Calling recursive function and subtracting
1 as it counts partitions, not cuts.*/
return minPartitions(0, n, s, dp) - 1;
}
public static void main(String[] args) {
String str = "BABABCBADCEDE";
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("The minimum number of partitions: " + sol.minCut(str));
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354
class Solution:
# Function to check if substring is a palindrome.
def isPalindrome(self, i, j, s):
while i < j:
if s[i] != s[j]:
return False
i += 1
j -= 1
return True
""" Recursive function to find the minimum
number of partitions to make palindromes."""
def minPartitions(self, i, n, s, dp):
# Base case: If we've reached the end of string.
if i == n:
return 0
# Check if the subproblem is already solved
if dp[i] != -1:
return dp[i]
minCost = float('inf')
""" Consider all possible substrings
starting from the current index."""
for j in range(i, n):
if self.isPalindrome(i, j, s):
""" If the substring is a palindrome,
calculate the cost and minimize it."""
cost = 1 + self.minPartitions(j + 1, n, s, dp)
minCost = min(minCost, cost)
# Return the result
dp[i] = minCost
return minCost
""" Main function to find the minimum number
of partitions for palindrome partitioning."""
def minCut(self, s):
n = len(s)
dp = [-1] * n
""" Calling recursive function and subtracting
1 as it counts partitions, not cuts."""
return self.minPartitions(0, n, s, dp) - 1
if __name__ == "__main__":
str = "BABABCBADCEDE"
# Create an instance of Solution class
sol = Solution()
# Print the result
print("The minimum number of partitions:", sol.minCut(str))
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
class Solution {
// Function to check if substring is a palindrome.
isPalindrome(i, j, s) {
while (i < j) {
if (s[i] !== s[j]) return false;
i++;
j--;
}
return true;
}
/* Recursive function to find the minimum
number of partitions to make palindromes.*/
minPartitions(i, n, str, dp) {
// Base case: If we've reached the end of string.
if (i === n) return 0;
// Check if the subproblem is already solved
if (dp[i] !== -1) return dp[i];
let minCost = Number.MAX_VALUE;
/* Consider all possible substrings
starting from the current index.*/
for (let j = i; j < n; j++) {
if (this.isPalindrome(i, j, str)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
let cost = 1 + this.minPartitions(j + 1, n, str, dp);
minCost = Math.min(minCost, cost);
}
}
// Return the result
dp[i] = minCost;
return minCost;
}
/* Main function to find the minimum number
of partitions for palindrome partitioning.*/
minCut(s) {
let n = s.length;
let dp = new Array(n).fill(-1);
/* Calling recursive function and subtracting
1 as it counts partitions, not cuts.*/
return this.minPartitions(0, n, s, dp) - 1;
}
}
const str = "BABABCBADCEDE";
// Create an instance of Solution class
const sol = new Solution();
// Print the result
console.log("The minimum number of partitions:", sol.minCut(str));
Complexity Analysis:
Time Complexity: O(N2), There are a total of N states and inside each state, a loop of size N(apparently) is running.Space Complexity:O(N) + Auxiliary stack space O(N), The first O(N) is for the dp array of size N.
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n+1]: Here, as we need to check dp[j+1] every time, the function will give a runtime error if j = n-1. To avoid this, we will take the array size as n+1 instead of n.
- Handle the base case: We knew in the recursive code the base case was when i == n, it meant that there were no characters left, we were returning 0. So, to cover this case we can initialize the entire dp array with 0.
- Next, memoization is a top-down approach, whereas tabulation is bottom-up. Our changing parameter i will change in opposite directions, i.e i will change from n-1→0.
- After that, copy down the recursive logic inside the nested loops to get the tabulation code.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
// Function to check if substring is a palindrome.
bool isPalindrome(int i, int j, string &s) {
while (i < j) {
if (s[i] != s[j]) return false;
i++;
j--;
}
return true;
}
public:
/* Function to find the minimum number
of partitions for palindrome partitioning.*/
int minCut(string s) {
int n = s.size();
/* Create a DP array to store
the minimum number of partitions.*/
vector<int> dp(n + 1, 0);
// Initialize the last element to 0.
dp[n] = 0;
// Loop through the string in reverse order.
for (int i = n - 1; i >= 0; i--) {
int minCost = INT_MAX;
/* Consider all possible substrings
starting from the current index.*/
for (int j = i; j < n; j++) {
if (isPalindrome(i, j, s)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
int cost = 1 + dp[j + 1];
minCost = min(minCost, cost);
}
}
dp[i] = minCost;
}
// Subtract 1 as it counts partitions, not cuts.
return dp[0] - 1;
}
};
int main() {
string str = "BABABCBADCEDE";
//Create an instance of Solution class
Solution sol;
cout << "The minimum number of partitions: " << sol.minCut(str) << "\n";
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
import java.util.*;
class Solution {
// Function to check if substring is a palindrome.
private boolean isPalindrome(int i, int j, String s) {
while (i < j) {
if (s.charAt(i) != s.charAt(j)) return false;
i++;
j--;
}
return true;
}
/* Function to find the minimum number
of partitions for palindrome partitioning.*/
public int minCut(String s) {
int n = s.length();
/* Create a DP array to store
the minimum number of partitions.*/
int[] dp = new int[n + 1];
// Initialize the last element to 0.
dp[n] = 0;
// Loop through the string in reverse order.
for (int i = n - 1; i >= 0; i--) {
int minCost = Integer.MAX_VALUE;
/* Consider all possible substrings
starting from the current index.*/
for (int j = i; j < n; j++) {
if (isPalindrome(i, j, s)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
int cost = 1 + dp[j + 1];
minCost = Math.min(minCost, cost);
}
}
dp[i] = minCost;
}
// Subtract 1 as it counts partitions, not cuts.
return dp[0] - 1;
}
public static void main(String[] args) {
String str = "BABABCBADCEDE";
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("The minimum number of partitions: " + sol.minCut(str));
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849
class Solution:
# Function to check if substring is a palindrome.
def isPalindrome(self, i, j, s):
while i < j:
if s[i] != s[j]:
return False
i += 1
j -= 1
return True
""" Function to find the minimum number
of partitions for palindrome partitioning."""
def minCut(self, s):
n = len(s)
""" Create a DP array to store
the minimum number of partitions."""
dp = [0] * (n + 1)
# Initialize the last element to 0.
dp[n] = 0
# Loop through the string in reverse order.
for i in range(n - 1, -1, -1):
minCost = float('inf')
""" Consider all possible substrings
starting from the current index."""
for j in range(i, n):
if self.isPalindrome(i, j, s):
""" If the substring is a palindrome,
calculate the cost and minimize it."""
cost = 1 + dp[j + 1]
minCost = min(minCost, cost)
dp[i] = minCost
# Subtract 1 as it counts partitions, not cuts.
return dp[0] - 1
if __name__ == "__main__":
str = "BABABCBADCEDE"
# Create an instance of Solution class
sol = Solution()
# Print the result
print("The minimum number of partitions:", sol.minCut(str))
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
class Solution {
// Function to check if substring is a palindrome.
isPalindrome(i, j, s) {
while (i < j) {
if (s[i] !== s[j]) return false;
i++;
j--;
}
return true;
}
/* Function to find the minimum number
of partitions for palindrome partitioning.*/
minCut(s) {
let n = s.length;
/* Create a DP array to store
the minimum number of partitions.*/
let dp = new Array(n + 1).fill(0);
// Initialize the last element to 0.
dp[n] = 0;
// Loop through the string in reverse order.
for (let i = n - 1; i >= 0; i--) {
let minCost = Number.MAX_VALUE;
/* Consider all possible substrings
starting from the current index.*/
for (let j = i; j < n; j++) {
if (this.isPalindrome(i, j, s)) {
/* If the substring is a palindrome,
calculate the cost and minimize it.*/
let cost = 1 + dp[j + 1];
minCost = Math.min(minCost, cost);
}
}
dp[i] = minCost;
}
// Subtract 1 as it counts partitions, not cuts.
return dp[0] - 1;
}
}
const str = "BABABCBADCEDE";
// Create an instance of Solution class
const sol = new Solution();
// Print the result
console.log("The minimum number of partitions:", sol.minCut(str));
Complexity Analysis:
Time Complexity:O(N2), There are a total of N states and inside each state a loop of size N(apparently) is running.Space Complexity:O(N), O(N) is for the dp array we have used.
Frequently Occurring Doubts
Q: Why does dp[i] = min(dp[j] + 1) work?
A: It ensures that the previous partition s[0:j] had the minimum cuts before the next valid palindrome.
Q: Why does dp[i] = 0 if s[0:i] is already a palindrome?
A: A full palindrome requires zero cuts, so no further partitions are needed.
Interview Followup Questions
Q: How would this problem change if we allowed k non-palindromic partitions?
A: Track k partitions and extend DP to include a k constraint.
Q: What if we needed to partition into exactly k palindromic substrings?
A: Use Multi-dimensional DP (dp[i][k]), ensuring exactly k partitions.
Notes
Code
✅ Testcase
Input: {'s': 'aab'}
Expected:
1
1
Actual: -
Time: -
sec
Status: Waiting
Input: {'s': 'abaaba'}
Expected:
0
0
Actual: -
Time: -
sec
Status: Waiting
Input: {'s': 'aabccbdee'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting
Facts
- • This kind of problem or its underlying approach is often used in text processing software and algorithms, such as spell-checkers or text editors
- • Detecting palindromes or structuring information in a way that allows for efficient checks is crucial in natural language processing tasks
- • For example, similar strategies are used in auto-correct systems in modern smartphones and word processing software to suggest the smallest number of changes to make in order to turn a misspelled word into a correct one