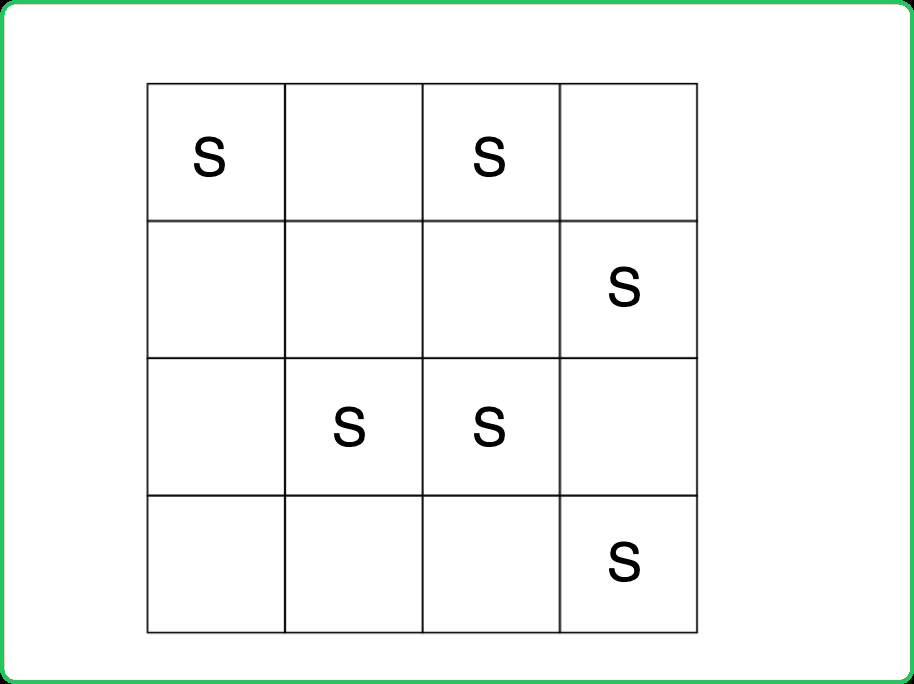
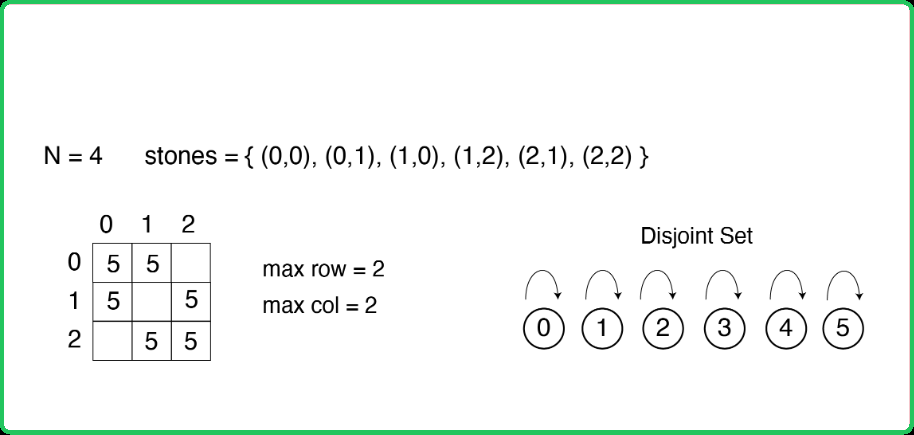
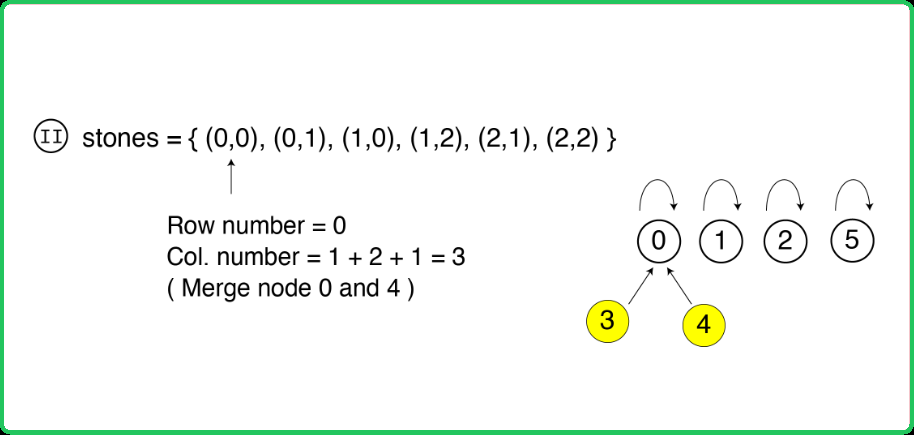
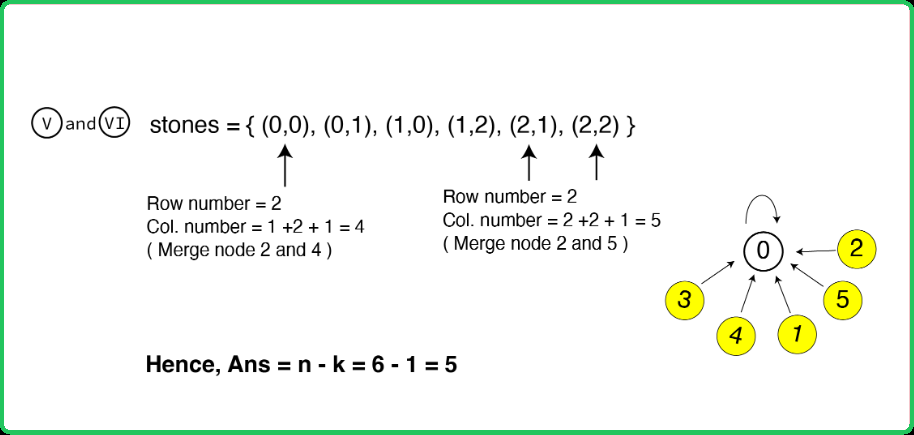
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139
#include <bits/stdc++.h>
using namespace std;
class DisjointSet {
public:
/* To store the ranks, parents and
sizes of different set of vertices */
vector<int> rank, parent, size;
// Constructor
DisjointSet(int n) {
rank.resize(n + 1, 0);
parent.resize(n + 1);
size.resize(n + 1);
for (int i = 0; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// Function to find ultimate parent
int findUPar(int node) {
if (node == parent[node])
return node;
return parent[node] = findUPar(parent[node]);
}
// Function to implement union by rank
void unionByRank(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (rank[ulp_u] < rank[ulp_v]) {
parent[ulp_u] = ulp_v;
}
else if (rank[ulp_v] < rank[ulp_u]) {
parent[ulp_v] = ulp_u;
}
else {
parent[ulp_v] = ulp_u;
rank[ulp_u]++;
}
}
// Function to implement union by size
void unionBySize(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (size[ulp_u] < size[ulp_v]) {
parent[ulp_u] = ulp_v;
size[ulp_v] += size[ulp_u];
}
else {
parent[ulp_v] = ulp_u;
size[ulp_u] += size[ulp_v];
}
}
};
// Solution class
class Solution{
public:
// Function to remove maximum stones
int maxRemove(vector<vector<int>>& stones, int n) {
/* To store the maximum row
and column having a stone */
int maxRow = 0;
int maxCol = 0;
// Iterate on all the nodes
for (auto it : stones) {
maxRow = max(maxRow, it[0]);
maxCol = max(maxCol, it[1]);
}
// Disjoint Set data structure
DisjointSet ds(maxRow + maxCol + 1);
// To store the nodes having a stone in Disjoint Set
unordered_map<int, int> stoneNodes;
// Iterate on all stones
for (auto it : stones) {
// Row number
int nodeRow = it[0];
// Converted column number
int nodeCol = it[1] + maxRow + 1;
// United two nodes
ds.unionBySize(nodeRow, nodeCol);
// Add the nodes to the map
stoneNodes[nodeRow] = 1;
stoneNodes[nodeCol] = 1;
}
// To store the number of connected components
int k = 0;
// Iterate on the set
for (auto it : stoneNodes) {
/* Increment the count if
a new component is found */
if (ds.findUPar(it.first) == it.first) {
k++;
}
}
// Return the answer
return n - k;
}
};
int main() {
int n = 6;
vector<vector<int>> stones = {
{0, 0}, {0, 1}, {1, 0},
{1, 2}, {2, 1}, {2, 2}
};
// Creating instance of Solution class
Solution sol;
/* Function call to get the
size of the largest island */
int ans = sol.maxRemove(stones, n);
// Output
cout << "The size of the largest island is: " << ans;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133
import java.util.*;
class DisjointSet {
/* To store the ranks, parents and
sizes of different set of vertices */
int[] rank, parent, size;
// Constructor
DisjointSet(int n) {
rank = new int[n + 1];
parent = new int[n + 1];
size = new int[n + 1];
for (int i = 0; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// Function to find ultimate parent
int findUPar(int node) {
if (node == parent[node])
return node;
return parent[node] = findUPar(parent[node]);
}
// Function to implement union by rank
void unionByRank(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (rank[ulp_u] < rank[ulp_v]) {
parent[ulp_u] = ulp_v;
}
else if (rank[ulp_v] < rank[ulp_u]) {
parent[ulp_v] = ulp_u;
}
else {
parent[ulp_v] = ulp_u;
rank[ulp_u]++;
}
}
// Function to implement union by size
void unionBySize(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (size[ulp_u] < size[ulp_v]) {
parent[ulp_u] = ulp_v;
size[ulp_v] += size[ulp_u];
}
else {
parent[ulp_v] = ulp_u;
size[ulp_u] += size[ulp_v];
}
}
}
// Solution class
class Solution {
// Function to remove maximum stones
public int maxRemove(int[][] stones, int n) {
/* To store the maximum row
and column having a stone */
int maxRow = 0;
int maxCol = 0;
// Iterate on all the nodes
for (int[] stone : stones) {
maxRow = Math.max(maxRow, stone[0]);
maxCol = Math.max(maxCol, stone[1]);
}
// Disjoint Set data structure
DisjointSet ds =
new DisjointSet(maxRow + maxCol + 1);
// To store the nodes having a stone in Disjoint Set
Map<Integer, Integer> stoneNodes = new HashMap<>();
// Iterate on all stones
for (int[] stone : stones) {
// Row number
int nodeRow = stone[0];
// Converted column number
int nodeCol = stone[1] + maxRow + 1;
// United two nodes
ds.unionBySize(nodeRow, nodeCol);
// Add the nodes to the map
stoneNodes.put(nodeRow, 1);
stoneNodes.put(nodeCol, 1);
}
// To store the number of connected components
int k = 0;
// Iterate on the set
for (int key : stoneNodes.keySet()) {
/* Increment the count if
a new component is found */
if (ds.findUPar(key) == key) {
k++;
}
}
// Return the answer
return n - k;
}
public static void main(String[] args) {
int n = 6;
int[][] stones = {
{0, 0}, {0, 1}, {1, 0},
{1, 2}, {2, 1}, {2, 2}
};
// Creating instance of Solution class
Solution sol = new Solution();
/* Function call to get the
size of the largest island */
int ans = sol.maxRemove(stones, n);
// Output
System.out.println("The size of the largest island is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105
class DisjointSet:
# To store the ranks, parents and
# sizes of different set of vertices
def __init__(self, n):
self.rank = [0] * (n + 1)
self.parent = [i for i in range(n + 1)]
self.size = [1] * (n + 1)
# Function to find ultimate parent
def findUPar(self, node):
if node == self.parent[node]:
return node
self.parent[node] = self.findUPar(self.parent[node])
return self.parent[node]
# Function to implement union by rank
def unionByRank(self, u, v):
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
if ulp_u == ulp_v:
return
if self.rank[ulp_u] < self.rank[ulp_v]:
self.parent[ulp_u] = ulp_v
elif self.rank[ulp_v] < self.rank[ulp_u]:
self.parent[ulp_v] = ulp_u
else:
self.parent[ulp_v] = ulp_u
self.rank[ulp_u] += 1
# Function to implement union by size
def unionBySize(self, u, v):
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
if ulp_u == ulp_v:
return
if self.size[ulp_u] < self.size[ulp_v]:
self.parent[ulp_u] = ulp_v
self.size[ulp_v] += self.size[ulp_u]
else:
self.parent[ulp_v] = ulp_u
self.size[ulp_u] += self.size[ulp_v]
# Solution class
class Solution:
# Function to remove maximum stones
def maxRemove(self, stones, n):
# To store the maximum row and column having a stone
maxRow = 0
maxCol = 0
# Iterate on all the nodes
for it in stones:
maxRow = max(maxRow, it[0])
maxCol = max(maxCol, it[1])
# Disjoint Set data structure
ds = DisjointSet(maxRow + maxCol + 1)
# To store the nodes having a stone in Disjoint Set
stoneNodes = {}
# Iterate on all stones
for it in stones:
# Row number
nodeRow = it[0]
# Converted column number
nodeCol = it[1] + maxRow + 1
# United two nodes
ds.unionBySize(nodeRow, nodeCol)
# Add the nodes to the map
stoneNodes[nodeRow] = 1
stoneNodes[nodeCol] = 1
# To store the number of connected components
k = 0
# Iterate on the set
for key in stoneNodes:
# Increment the count if a new component is found
if ds.findUPar(key) == key:
k += 1
# Return the answer
return n - k
# Main function to test the Solution class
if __name__ == "__main__":
n = 6
stones = [
[0, 0], [0, 1], [1, 0],
[1, 2], [2, 1], [2, 2]
]
# Creating instance of Solution class
sol = Solution()
# Function call to get the size of the largest island
ans = sol.maxRemove(stones, n)
# Output
print("The size of the largest island is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117
class DisjointSet {
// Constructor
constructor(n) {
/* To store the ranks, parents and sizes
of different set of vertices */
this.rank = new Array(n + 1).fill(0);
this.parent = new Array(n + 1).fill(0).map((_, i) => i);
this.size = new Array(n + 1).fill(1);
}
// Function to find ultimate parent
findUPar(node) {
if (node === this.parent[node]) return node;
this.parent[node] = this.findUPar(this.parent[node]);
return this.parent[node];
}
// Function to implement union by rank
unionByRank(u, v) {
const ulp_u = this.findUPar(u);
const ulp_v = this.findUPar(v);
if (ulp_u === ulp_v) return;
if (this.rank[ulp_u] < this.rank[ulp_v]) {
this.parent[ulp_u] = ulp_v;
} else if (this.rank[ulp_v] < this.rank[ulp_u]) {
this.parent[ulp_v] = ulp_u;
} else {
this.parent[ulp_v] = ulp_u;
this.rank[ulp_u]++;
}
}
// Function to implement union by size
unionBySize(u, v) {
const ulp_u = this.findUPar(u);
const ulp_v = this.findUPar(v);
if (ulp_u === ulp_v) return;
if (this.size[ulp_u] < this.size[ulp_v]) {
this.parent[ulp_u] = ulp_v;
this.size[ulp_v] += this.size[ulp_u];
} else {
this.parent[ulp_v] = ulp_u;
this.size[ulp_u] += this.size[ulp_v];
}
}
}
// Solution class
class Solution {
// Function to remove maximum stones
maxRemove(stones, n) {
// To store the maximum row and column having a stone
let maxRow = 0;
let maxCol = 0;
// Iterate on all the nodes
for (const it of stones) {
maxRow = Math.max(maxRow, it[0]);
maxCol = Math.max(maxCol, it[1]);
}
// Disjoint Set data structure
const ds = new DisjointSet(maxRow + maxCol + 1);
// To store the nodes having a stone in Disjoint Set
const stoneNodes = new Map();
// Iterate on all stones
for (const it of stones) {
// Row number
const nodeRow = it[0];
// Converted column number
const nodeCol = it[1] + maxRow + 1;
// United two nodes
ds.unionBySize(nodeRow, nodeCol);
// Add the nodes to the map
stoneNodes.set(nodeRow, 1);
stoneNodes.set(nodeCol, 1);
}
// To store the number of connected components
let k = 0;
// Iterate on the set
for (const key of stoneNodes.keys()) {
// Increment the count if a new component is found
if (ds.findUPar(key) === key) {
k++;
}
}
// Return the answer
return n - k;
}
}
// Main function to test the Solution class
(function main() {
const n = 6;
const stones = [
[0, 0], [0, 1], [1, 0],
[1, 2], [2, 1], [2, 2]
];
// Creating instance of Solution class
const sol = new Solution();
// Function call to get the size of the largest island
const ans = sol.maxRemove(stones, n);
// Output
console.log("The size of the largest island is: " + ans);
})();
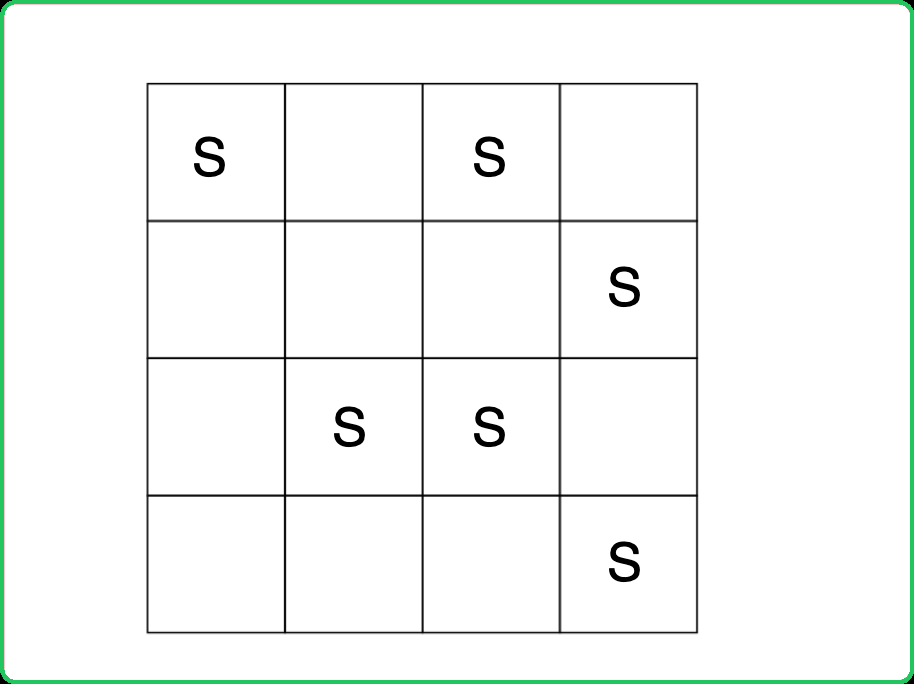
 Thus, the maximum number of stones that can be removed can be found if the number of connected components(k) in the graph is known.
Thus, the maximum number of stones that can be removed can be found if the number of connected components(k) in the graph is known.