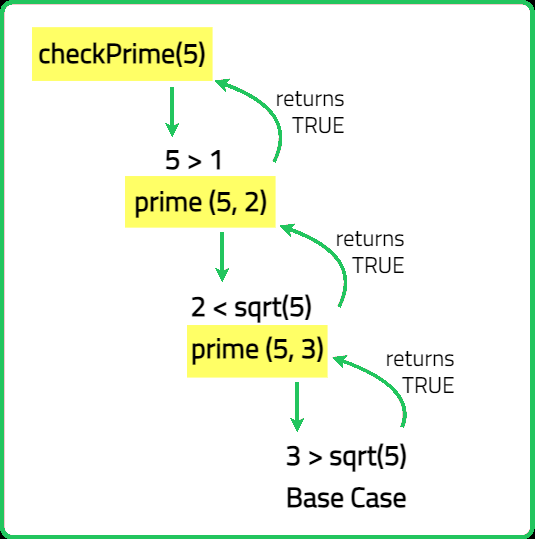
Check if a number is prime or not

Beginner Problems Basic Recursion Easy

Prime number checking, the underlying concept of this problem, is a crucial component in cryptography, particularly RSA algorithm, which is widely used in secure data transmission
The security of RSA is based on the practical difficulty of factoring the product of two large prime numbers, the factoring problem

Given an integer num, return true if it is prime otherwise false.

A prime number is a number that is divisible only by 1 and itself.

Examples:

Input : num = 5

Output : true

Explanation : The factors of 5 are 1 and 5 only.

So it satisfies the prime number condition.

Input : num = 15

Output : false

Explanation : The factors of 15 are 1, 3, 5, 15 only.

As the number has factors other than 1 and itself, So it is not a prime number.

Input : num = 41

Constraints

1 <= num <= 10⁴

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

Intuition

To check if a number is prime, determine if it has any divisors other than 1 and itself. Using recursion, systematically check for divisors from 2 up to the square root of the number. If any divisor within this range is found, the number is not prime. If no divisors are found by the time the square root of the number is reached, the number is prime.

Approach

First, handle the base cases: If the number is less than or equal to 1, return false because 0 and 1 are not prime. If the number is greater than 1, start checking for divisibility from 2.
Define a recursive helper function prime(num, x) where num is the number to be checked and x is the current divisor to check.
In the helper function --> if x is greater than the square root of num, return true indicating that num is a prime number. If num is divisible by x (i.e., num % x == 0), return false indicating that num is not a prime number. If neither condition is met, recursively call the function with the next divisor x + 1.

Dry Run

Solution

class Solution {
public:
    // Main method for testing the checkPrime function
    int main() {
        Solution solution;
        int num = 7; 
        bool result = solution.checkPrime(num); 
        cout << (result ? "Prime" : "Not Prime") << endl; 
        return 0;
    }

    bool checkPrime(int num) {
     // 0 and 1 are not prime numbers
        if (num <= 1) {
            return false;
        }
       // Call the helper function to check for primality
        return prime(num, 2); 
    }

private:
    bool prime(int num, int x) {
    // Base case: x > sqrt(num), so the number is prime
        if (x > sqrt(num)) {
            return true; 
        }

        if (num % x == 0) {
        // Found a divisor, so the number is not prime
            return false; 
        }
       // Recursive call with the next divisor
        return prime(num, x + 1); 
    }
};
class Solution {
    // Main method for testing the checkPrime function
    public static void main(String[] args) {
        Solution solution = new Solution();
        int num = 7; 
        boolean result = solution.checkPrime(num); 
        System.out.println(result); 
    }

    public boolean checkPrime(int num) {
    // 0 and 1 are not prime numbers
        if (num <= 1) {
            return false; 
        }
       // Call the helper function to check for primality
        return prime(num, 2); 
    }

    private boolean prime(int num, int x) {
        if (x > Math.sqrt(num)) {
            return true; 
        }
       // Found a divisor, so the number is not prime
        if (num % x == 0) {
            return false; 
        }
        // Recursive call with the next divisor
        return prime(num, x + 1); 
    }
}
class Solution:
    def checkPrime(self, num):
        if num <= 1:
            return False  # 0 and 1 are not prime numbers
        return self.prime(num, 2)  # Call the helper function to check for primality
    
    def prime(self, num, x):
       # Base case: x > sqrt(num), so the number is prime
        if x > num ** 0.5:
            return True  
        if num % x == 0:
        # Found a divisor, so the number is not prime
            return False  
         # Recursive call with the next divisor
        return self.prime(num, x + 1)  

# Main method for testing the checkPrime function
if __name__ == "__main__":
    solution = Solution()
    num = 7  
    result = solution.checkPrime(num)  
    print(result)  
class Solution {
    // Method to check if a number is prime
    checkPrime(num) {
        if (num <= 1) {
            return false; 
        }
        // Call the helper function to check for primality
        return this.prime(num, 2);  
    }

    // Helper method to check for primality using recursion
    prime(num, x) {
    // Base case: x > sqrt(num), so the number is prime
        if (x > Math.sqrt(num)) {
            return true;  
        }
        // Found a divisor, so the number is not prime
        if (num % x === 0) {
            return false;  
        }
        // Recursive call with the next divisor
        return this.prime(num, x + 1);  
    }
}

// Main method for testing the checkPrime function
const solution = new Solution();
const num = 7;  
const result = solution.checkPrime(num); 
console.log(result);  

Complexity Analysis

Time Complexity O(sqrt(N)) because we only need to check for divisors up to the square root of the number.

Space Complexity : O(sqrt(N)) due to the recursion stack depth which can grow up to the square root of the number.

Code

Problem List