Divisors of a number

Beginner Problems Basic Maths Easy

Fun Fact: The underlying concept from this problem, finding all the divisors of a number, is surprisingly important in cryptography, a critical part of information security
Specifically, it's used in the RSA encryption algorithm, which is widely implemented in communication protocols like HTTPS for secure data transmission over the internet
The algorithm uses two large prime numbers, whose product serves as a key
The security of RSA is based on the fact that, even knowing the product, it's difficult to determine the original primes (i
e
, find the divisors), particularly as the prime numbers used become larger

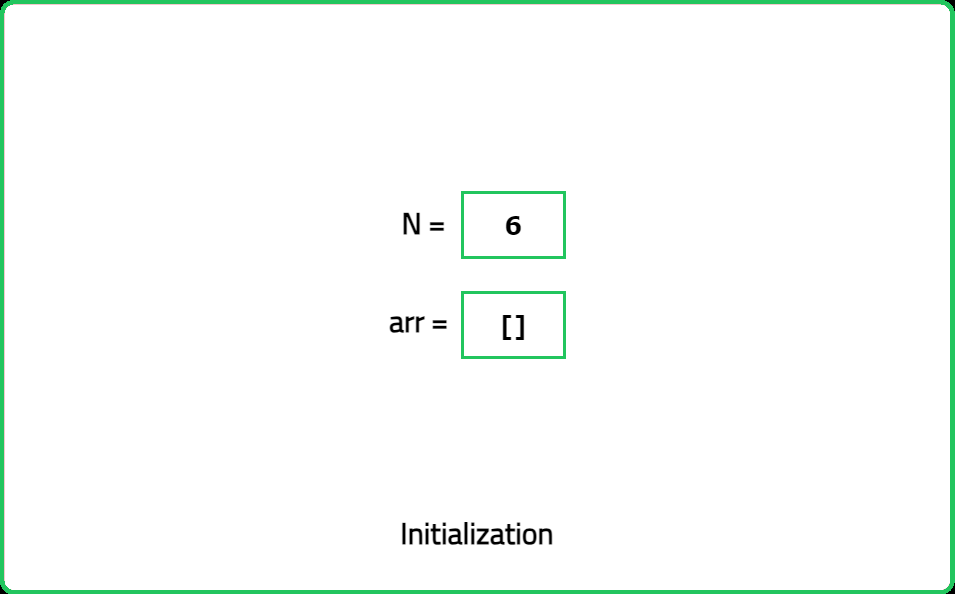
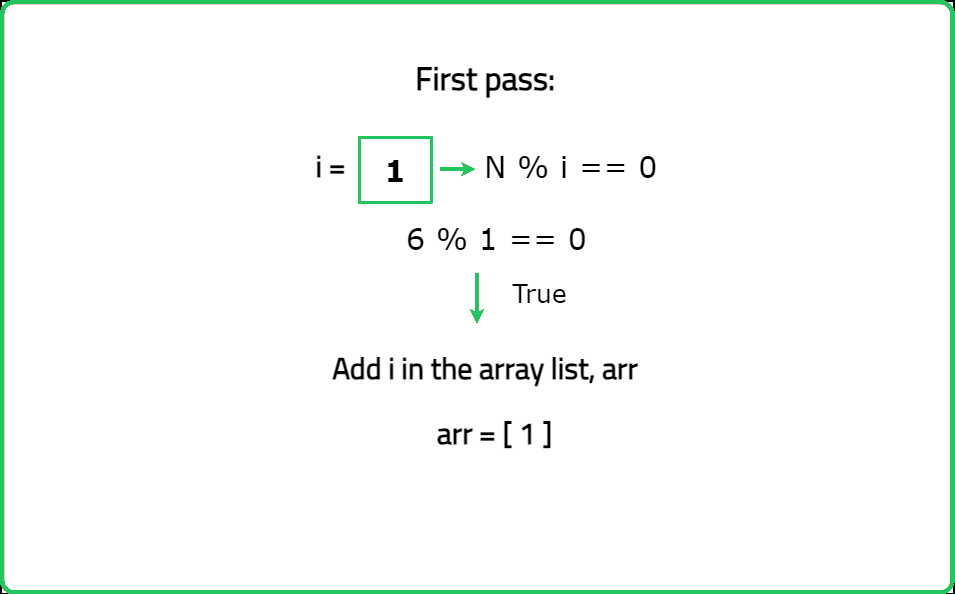
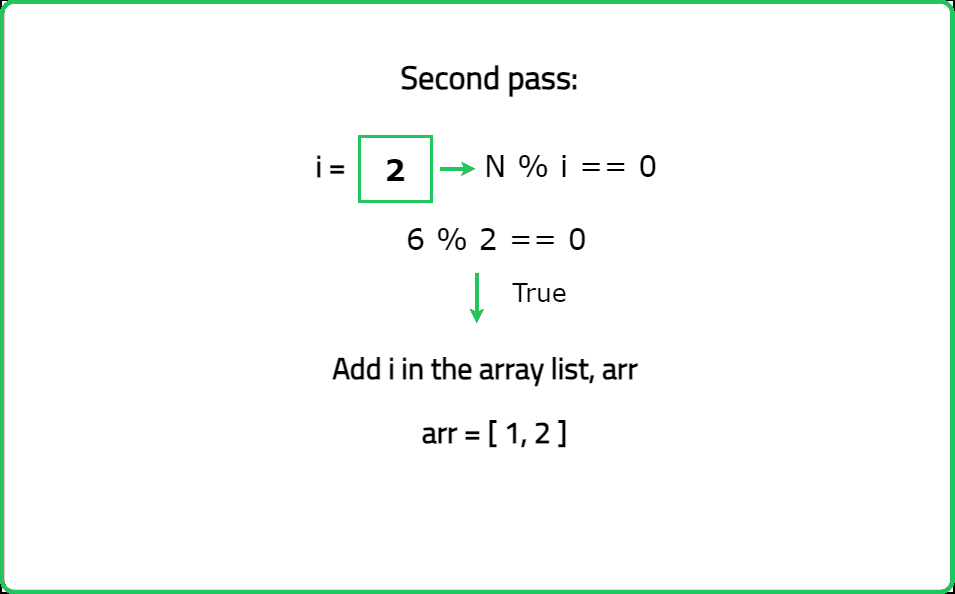
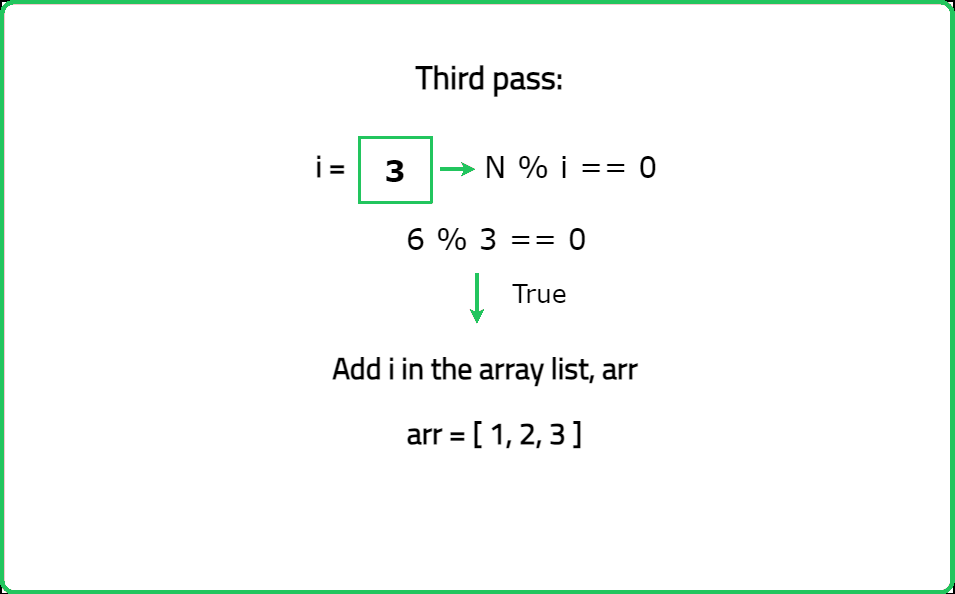
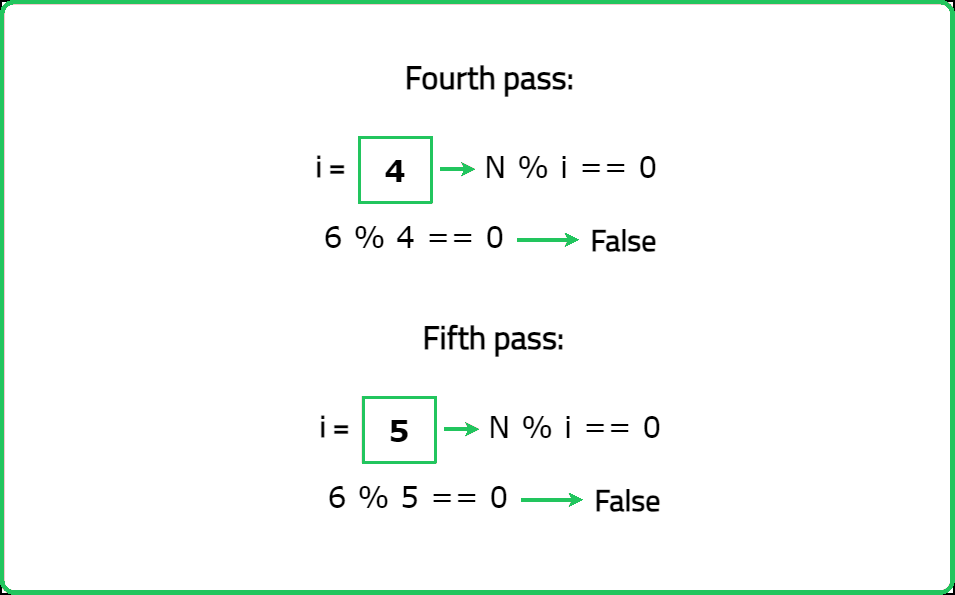
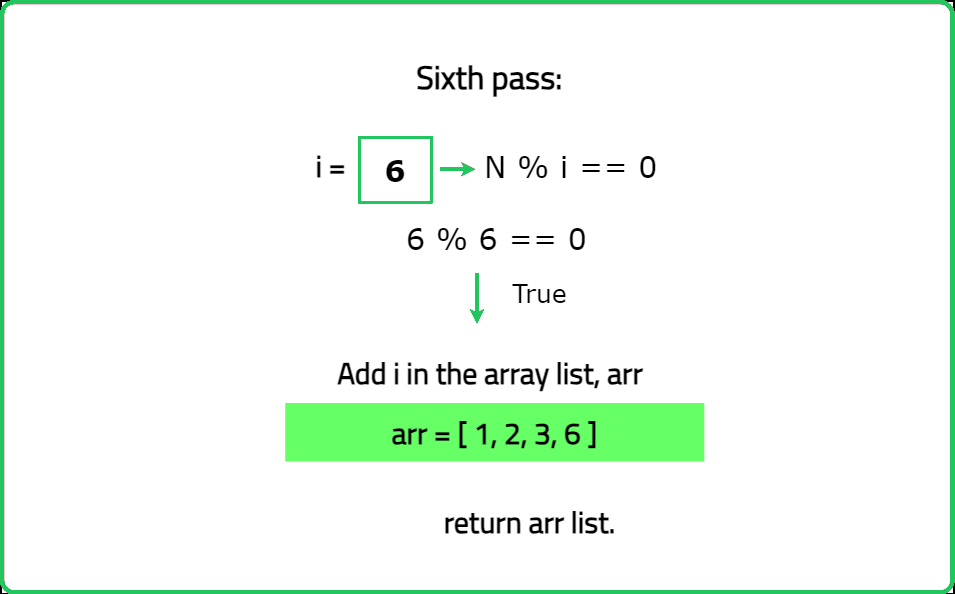
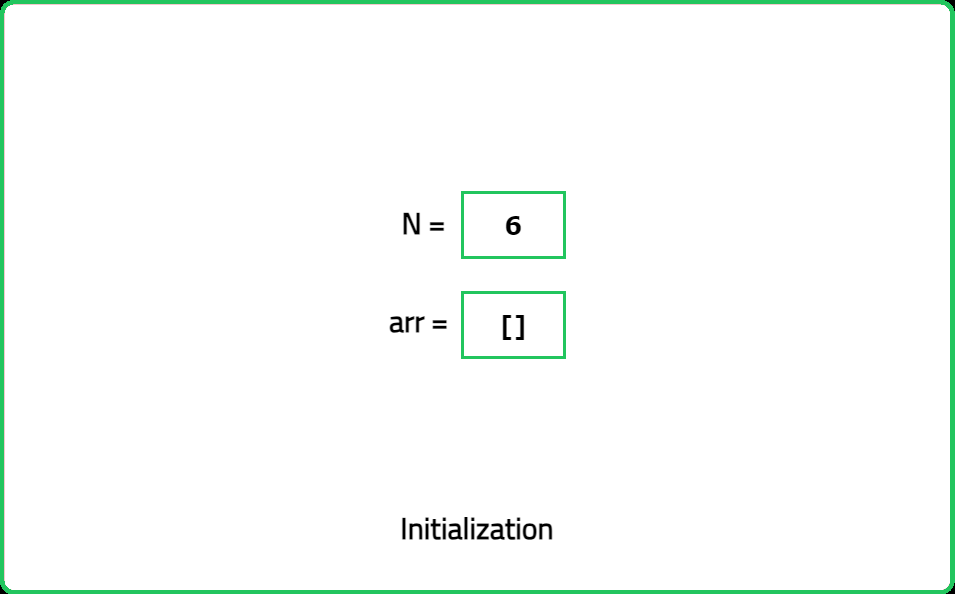
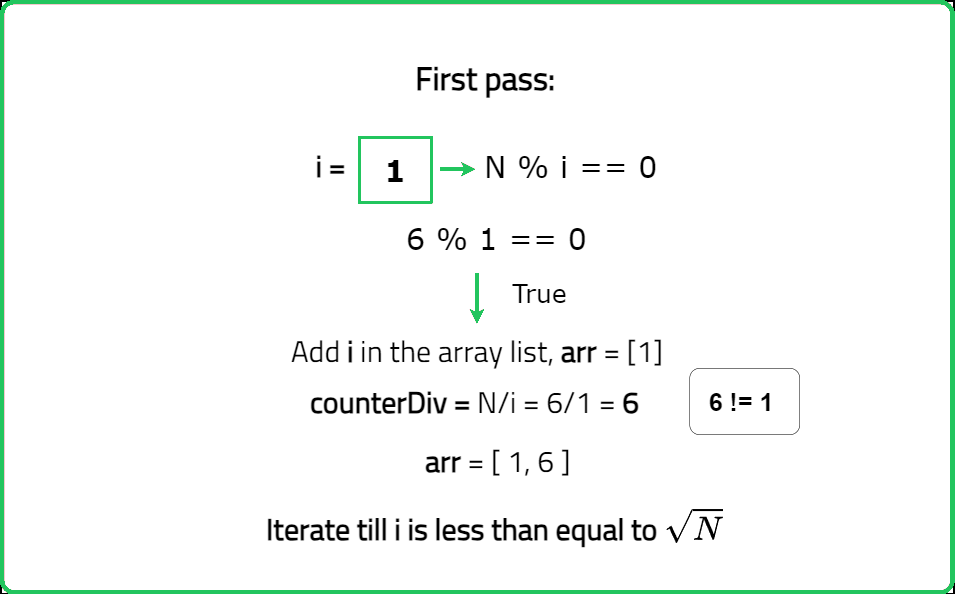
You are given an integer n. You need to find all the divisors of n. Return all the divisors of n as an array or list in a sorted order.

A number which completely divides another number is called it's divisor.

Examples:

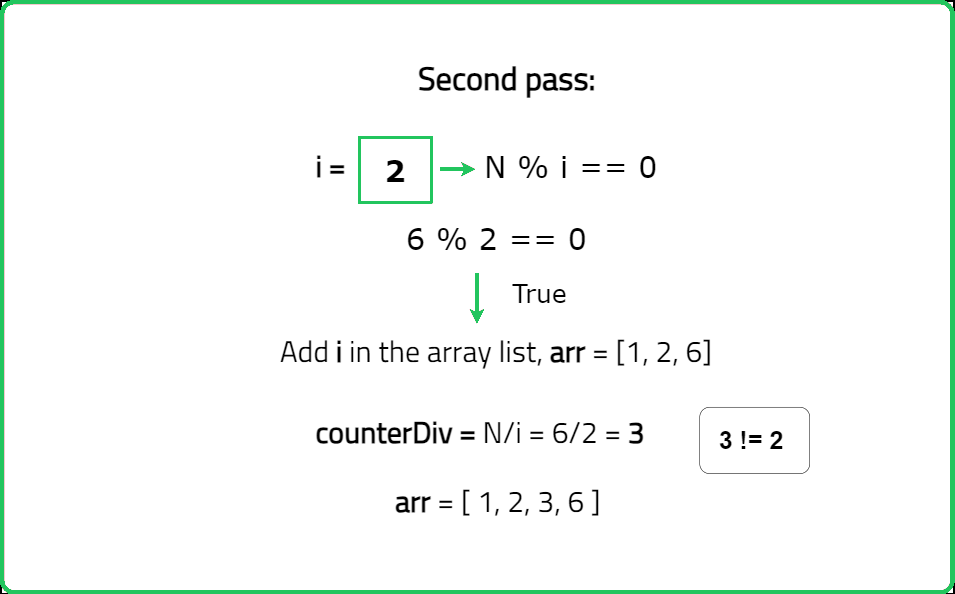
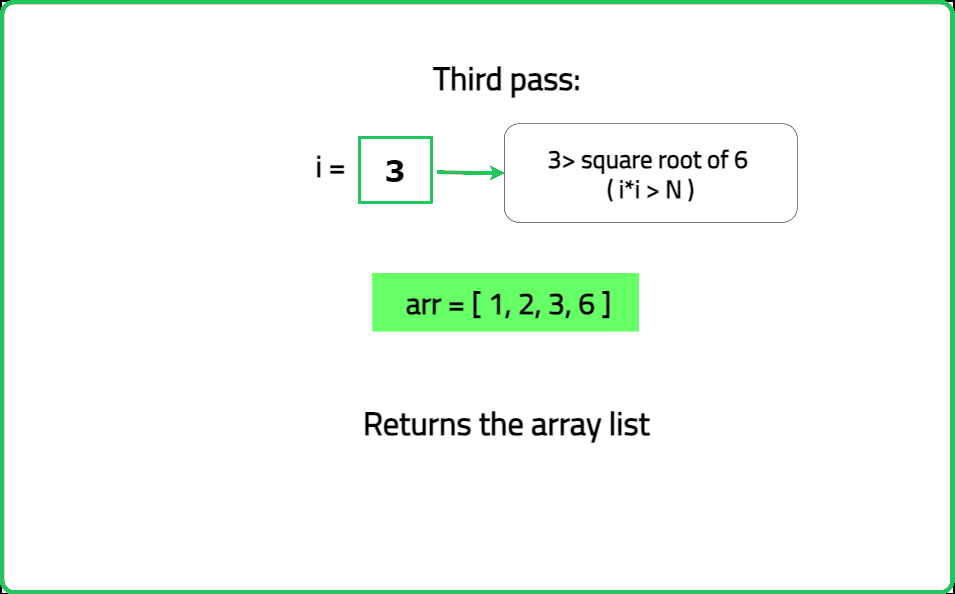
Input: n = 6

Output = [1, 2, 3, 6]

Explanation: The divisors of 6 are 1, 2, 3, 6.

Input: n = 8

Output: [1, 2, 4, 8]

Explanation: The divisors of 8 are 1, 2, 4, 8.

Input: n = 7

Constraints

1 <= n <= 1000

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

Intuition:

Given a number n, a brute force approach would be to iterate from 1 to n checking each value if it divides n without leaving a remainder. For each divisor found, store it in a list and return the result.

Approach:

Initialize an array/list to store the divisors.
Iterate from 1 to n, and check if the current value is a divisor of n or not. Add the value to the array/list if it is a divisor.
The array/list stores all the divisors of n.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to find all 
    divisors of n */
    vector<int> divisors(int n) {
        
        // To store the divisors;
        vector<int> ans;
        
        // Iterate from 1 to n
        for(int i=1; i <= n; i++) {
            
            // If a divisor is found
            if(n % i == 0) {
                //Add it to the answer
                ans.push_back(i);
            }
        }
        
        // Return the result
        return ans;
    }
};

int main()
{
    int n = 6;
    
    /* Creating and instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find 
    all divisors of n */
    vector<int> ans = sol.divisors(n);
    
    cout << "The divisors of " << n << " are: ";
    for(int i=0; i < ans.size(); i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}
import java.util.Arrays;

class Solution {
    /* Function to find all 
    divisors of n */
    public int[] divisors(int n) {
        
        // Initial size of the array is set to n
        int[] temp = new int[n];
        int count = 0;
        
        // Iterate from 1 to n
        for (int i = 1; i <= n; i++) {
            
            // If a divisor is found
            if (n % i == 0) {
                // Add it to the array
                temp[count++] = i;
            }
        }
        
        /* Copy the divisors to an 
        array of the exact size */
        int[] ans = Arrays.copyOf(temp, count);
        
        // Return the result
        return ans;
    }

    public static void main(String[] args) {
        int n = 6;
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution();
        
        /* Function call to find 
        all divisors of n */
        int[] ans = sol.divisors(n);
        
        System.out.print("The divisors of " + n + " are: ");
        for (int i = 0; i < ans.length; i++) {
            System.out.print(ans[i] + " ");
        }
    }
}
class Solution:
    # Function to find all
    # divisors of n
    def divisors(self, n):
        
        # To store the divisors
        ans = []
        
        # Iterate from 1 to n
        for i in range(1, n + 1):
            
            # If a divisor is found
            if n % i == 0:
                # Add it to the answer
                ans.append(i)
        
        # Return the result
        return ans

# Input number
n = 6

# Creating an instance of 
# Solution class
sol = Solution()

# Function call to find 
# all divisors of n
ans = sol.divisors(n)

print(f"The divisors of {n} are: ", end="")
for i in range(len(ans)):
    print(ans[i], end=" ")
class Solution {
    /* Function to find all 
    divisors of n */
    divisors(n) {
        
        // To store the divisors
        let ans = [];
        
        // Iterate from 1 to n
        for (let i = 1; i <= n; i++) {
            
            // If a divisor is found
            if (n % i === 0) {
                // Add it to the answer
                ans.push(i);
            }
        }
        
        // Return the result
        return ans;
    }
}

// Input number
let n = 6;

/* Creating an instance of 
Solution class */
let sol = new Solution();

/* Function call to find 
all divisors of n */
let ans = sol.divisors(n);

console.log(`The divisors of ${n} are: `, ans.join(" "));

Complexity Analysis:

Time Complexity: O(N) – Iterating N times, and performing constant time operations in each pass.

Space Complexity: O(sqrt(N)) – A number N can have at max 2*sqrt(N) divisors, which are stored in the array.

Intuition:

The previous approach can be optimized by using the property that for any non-negative integer n, if d is a divisor of n then n/d (known as counterpart divisor) is also a divisor of n.
This property is symmetric about the square root of n by traversing just the first half we can avoid redundant iteration and computations improving the efficiency of the algorithm.

Approach:

Initialize an array/list to store the divisors.
Iterate from 1 to sqrt(n), and check if the current value is a divisor of n or not. Add the value to the array/list if it is a divisor. Also, add the counterpart divisor to the array/list if it is different from the current divisor.
The array/list stores all the divisors of n. Sort the list and return the result.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to find all 
    divisors of n */
    vector<int> divisors(int n) {
        
        // To store the divisors;
        vector<int> ans;
        
        int sqrtN = sqrt(n);
        
        // Iterate from 1 to sqrtN
        for(int i=1; i <= sqrtN; i++) {
            
            // If a divisor is found
            if(n % i == 0) {
                //Add it to the answer
                ans.push_back(i);
                
                /* Add the counterpart divisor
                 if it's different from i */
                if(i != n / i) {
                    ans.push_back(n/i);
                }
            }
        }
        
        // Sorting the result 
        sort(ans.begin(), ans.end());
        
        // Return the result
        return ans;
    }
};

int main()
{
    int n = 6;
    
    /* Creating and instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find 
    all divisors of n */
    vector<int> ans = sol.divisors(n);
    
    cout << "The divisors of " << n << " are: ";
    for(int i=0; i < ans.size(); i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}
import java.util.Arrays;

class Solution {
    public int[] divisors(int n) {
        
        // To store the divisors
        int[] temp = new int[n]; // Temporary array with max possible size
        int count = 0;
        
        int sqrtN = (int) Math.sqrt(n);
        
        // Iterate from 1 to sqrtN
        for(int i = 1; i <= sqrtN; i++) {
            
            // If a divisor is found
            if(n % i == 0) {
                // Add it to the answer
                temp[count++] = i;
                
                /* Add the counterpart divisor
                 if it's different from i */
                if(i != n / i) {
                    temp[count++] = n / i;
                }
            }
        }
        
        // Copy only the filled part of temp to the result array
        int[] ans = Arrays.copyOf(temp, count);
        
        // Sorting the result 
        Arrays.sort(ans);
        
        // Return the result
        return ans;
    }

    public static void main(String[] args) {
        int n = 6;
        
        // Creating an instance of Solution class 
        Solution sol = new Solution(); 
        
        // Function call to find all divisors of n
        int[] ans = sol.divisors(n);
        
        System.out.print("The divisors of " + n + " are: ");
        for(int i = 0; i < ans.length; i++) {
            System.out.print(ans[i] + " ");
        }
    }
}
import math

class Solution:
    # Function to find all 
    # divisors of n
    def divisors(self, n):
        
        # To store the divisors
        ans = []
        
        sqrtN = int(math.sqrt(n))
        
        # Iterate from 1 to sqrtN
        for i in range(1, sqrtN + 1):
            
            # If a divisor is found
            if n % i == 0:
                # Add it to the answer
                ans.append(i)
                
                # Add the counterpart divisor
                # if it's different from i
                if i != n // i:
                    ans.append(n // i)
        
        # Sorting the result 
        ans.sort()
        
        # Return the result
        return ans

# Creating an instance of 
# Solution class 
sol = Solution()

n = 6

# Function call to find 
# all divisors of n
ans = sol.divisors(n)

print("The divisors of", n, "are:", " ".join(map(str, ans)))
class Solution {
    /* Function to find all 
    divisors of n */
    divisors(n) {
        
        // To store the divisors
        const ans = [];
        
        const sqrtN = Math.floor(Math.sqrt(n));
        
        // Iterate from 1 to sqrtN
        for(let i = 1; i <= sqrtN; i++) {
            
            // If a divisor is found
            if(n % i === 0) {
                // Add it to the answer
                ans.push(i);
                
                /* Add the counterpart divisor
                 if it's different from i */
                if(i !== n / i) {
                    ans.push(n / i);
                }
            }
        }
        
        // Sorting the result 
        ans.sort((a, b) => a - b);
        
        // Return the result
        return ans;
    }
}

// Creating an instance of 
// Solution class 
const sol = new Solution();

const n = 6;

/* Function call to find 
all divisors of n */
const ans = sol.divisors(n);

console.log("The divisors of " + n + " are: " + ans.join(" "));

Complexity Analysis:

Time Complexity: O(sqrt(N)) + O(K*Log(K)) – Iterating sqrt(N) times, and performing constant time operations in each pass to get all the divisors in the list. Sorting the list of divisors takes O(K*Log(K)) time where K is the number of divisors of the number.

Space Complexity: O(sqrt(N)) – A number N can have at max 2*sqrt(N) divisors, which are stored in the array.

Code

Problem List

Divisors of a number

Examples:

Constraints

Company Tags

Editorial

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Notes

Code