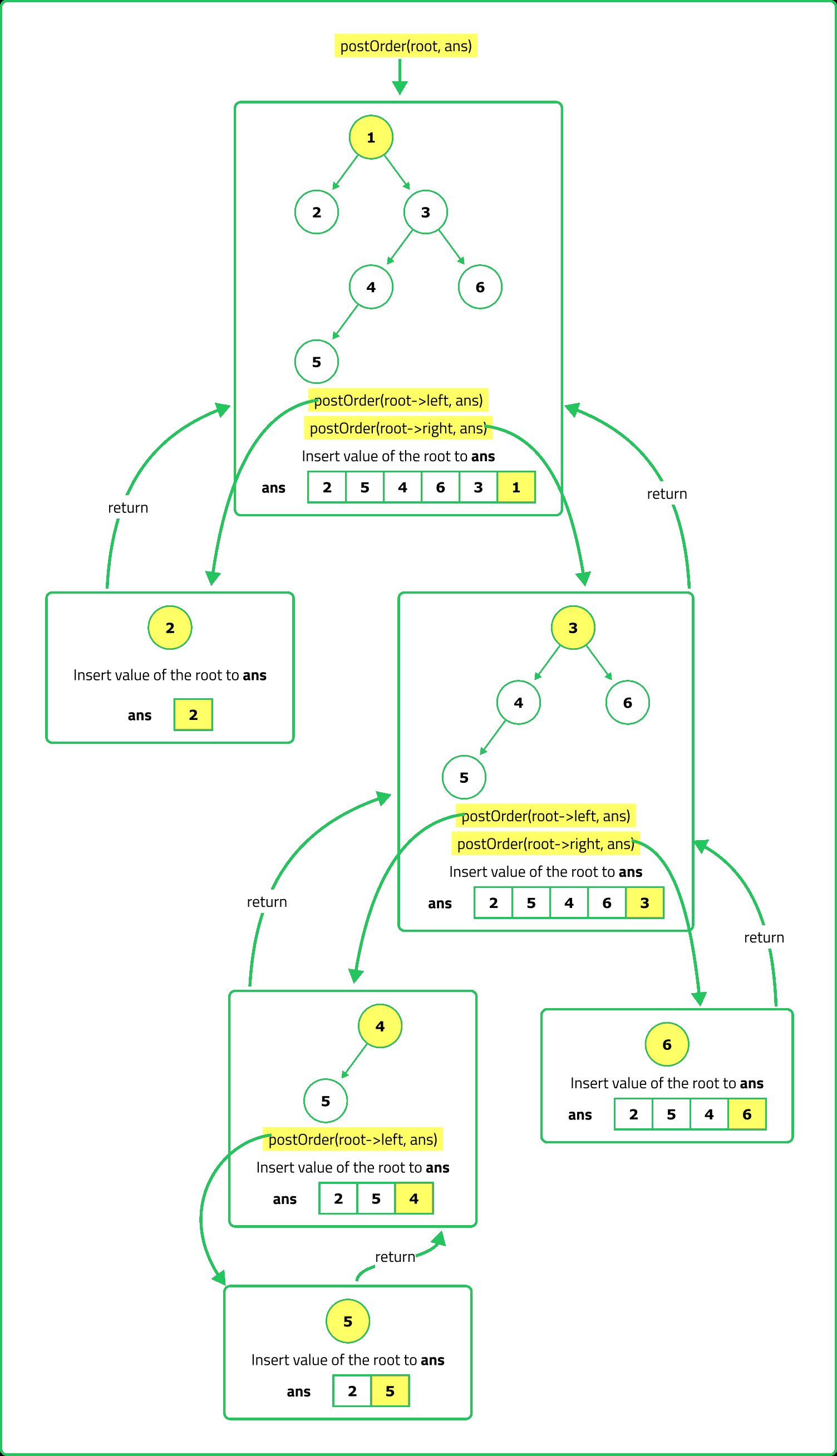
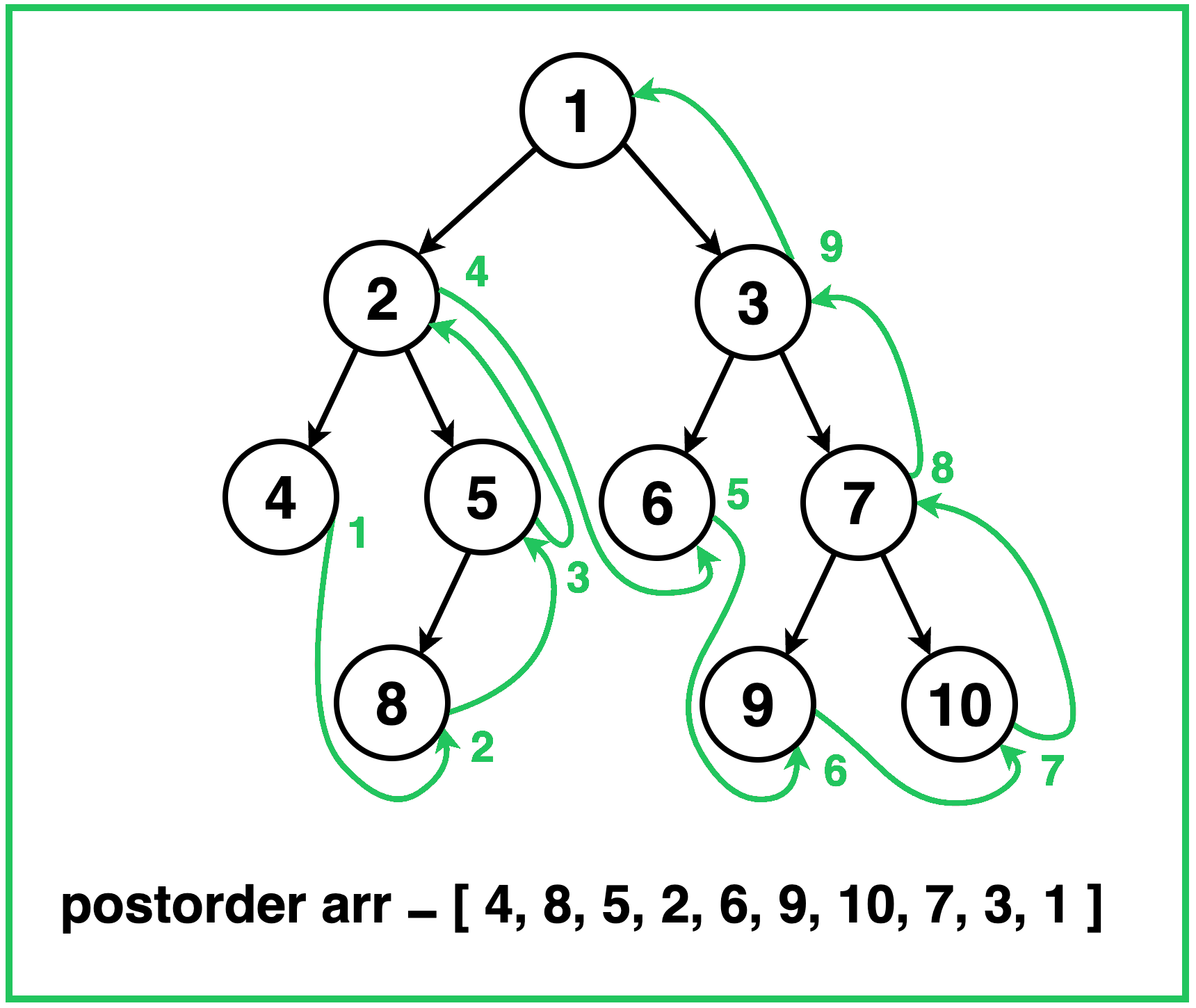
Postorder Traversal
Binary Trees
Theory/Traversals
Easy
- Binary tree traversal, including Postorder traversal, is a fundamental concept extensively used in practical software development
- For example, it's used in certain database operations (like DBMS), graphic algorithms (in game development), and hierarchical file systems (like in operating systems and file explorer applications) to visit data in a structured and orderly manner
- Postorder traversal can specifically be useful in certain mathematical calculations like expression tree evaluations, where the operation resides in the parent node and the operands are in the child nodes
- The postorder traversal ensures that the operands are evaluated before the operation is applied
Given root of binary tree, return the Postorder traversal of the binary tree.
Examples:
Input : root = [1, 4, null, 4, 2]
Output : [4, 2, 4, 1]
Explanation :
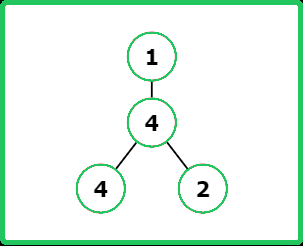
Input : root = [1, null, 2, 3]
Output : [3, 2, 1]
Explanation :
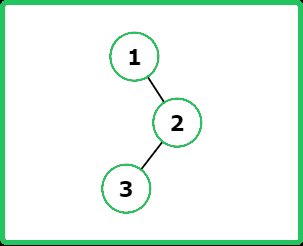
Input : root = [5, 1, 2, 8, null, 4, 5, null, 6]
Constraints
- 1 <= Number of Nodes <= 100
- -100 <= Node.val <= 100
Hints
- A stack can be used to simulate recursion manually. Since postorder requires processing root last, push elements in a modified preorder order. Root → Right → Left (instead of Root → Left → Right).
- Use one stack and a prev pointer to track whether traversal is moving up from left or right.
Company Tags
Twilio
Johnson & Johnson
McKinsey & Company
Zoho
Micron Technology
PwC
Shopify
Zynga
Riot Games
Bain & Company
Flipkart
Square
Reddit
Walmart
Intel
Lyft
Etsy
Cloudflare
DoorDash
Freshworks
Goldman Sachs
Philips Healthcare
KPMG
MongoDB
PayPal
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe