LFU Cache
- The concept of a Least Frequently Used (LFU) cache, as represented in this problem, is routinely used in database systems, web browser caching, and operating systems for page replacement
- The idea is to keep the most frequently accessed items in memory for faster retrieval
- For instance, web browsers like Chrome or Firefox use LFU to cache web pages
- When the cache is full, the least frequently viewed web pages are evicted to make room for new ones
- This makes returning to frequently visited sites much faster
Design and implement a data structure for a Least Frequently Used (LFU) cache.
Implement the LFUCache class with the following functions:
LFUCache(int capacity): Initialize the object with the specified capacity.
int get(int key): Retrieve the value of the key if it exists in the cache; otherwise, return -1.
void put(int key, int value): Update the value of the key if it is present in the cache, or insert the key if it is not already present. If the cache has reached its capacity, invalidate and remove the least frequently used key before inserting a new item. In case of a tie (i.e., two or more keys with the same frequency), invalidate the least recently used key.
A use counter is maintained for each key in the cache to determine the least frequently used key. The key with the smallest use counter is considered the least frequently used.
When a key is first inserted into the cache, its use counter is set to 1 due to the put operation. The use counter for a key in the cache is incremented whenever a get or put operation is called on it.
Ensure that the functions get and put run in O(1) average time complexity.
Examples:
Input:
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
Output:
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]
Explanation:
// cnt(x) = the use counter for key x
// cache=[] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=[1,_], cnt(1)=1
lfu.put(2, 2); // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=[1,2], cnt(2)=1, cnt(1)=2
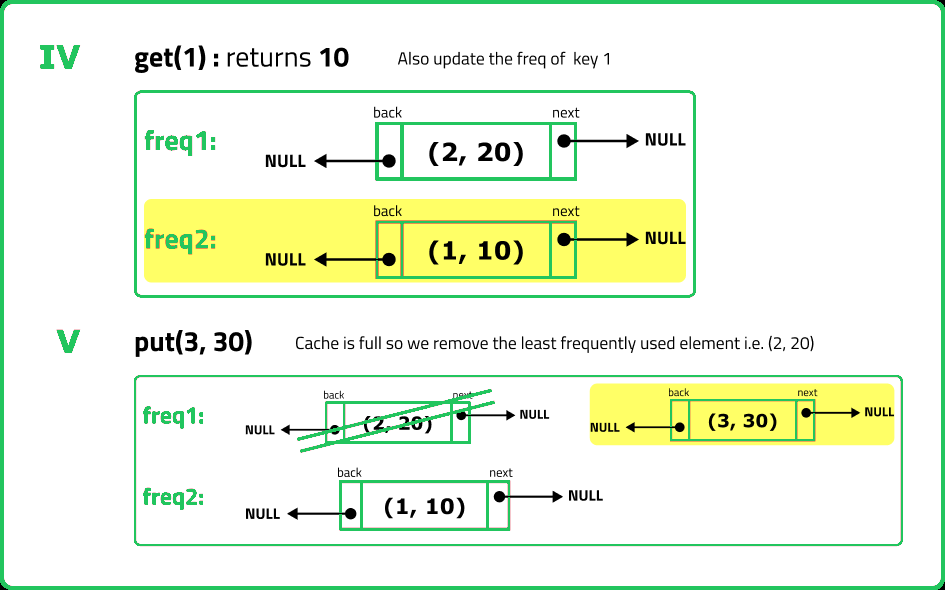
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=[3,1], cnt(3)=2, cnt(1)=2
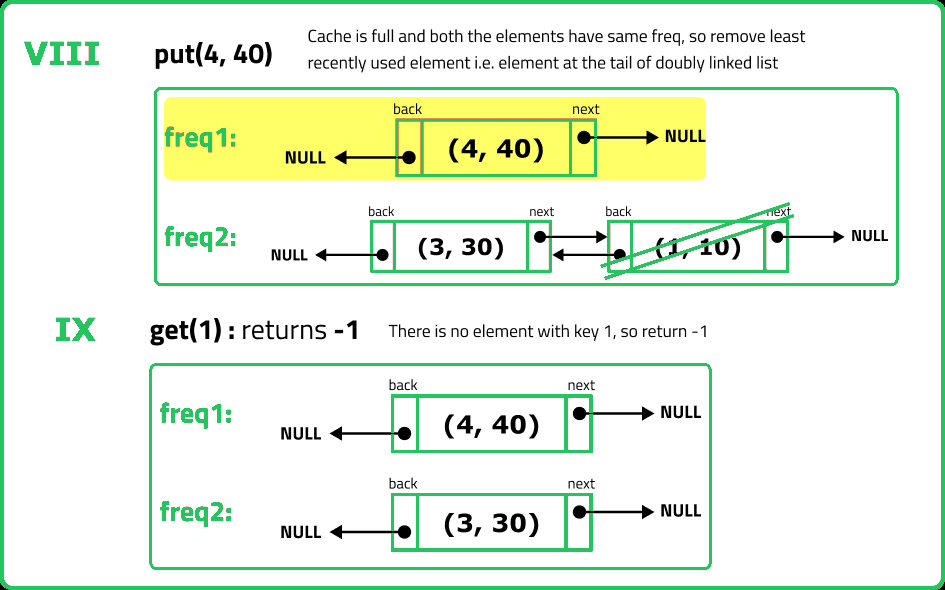
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
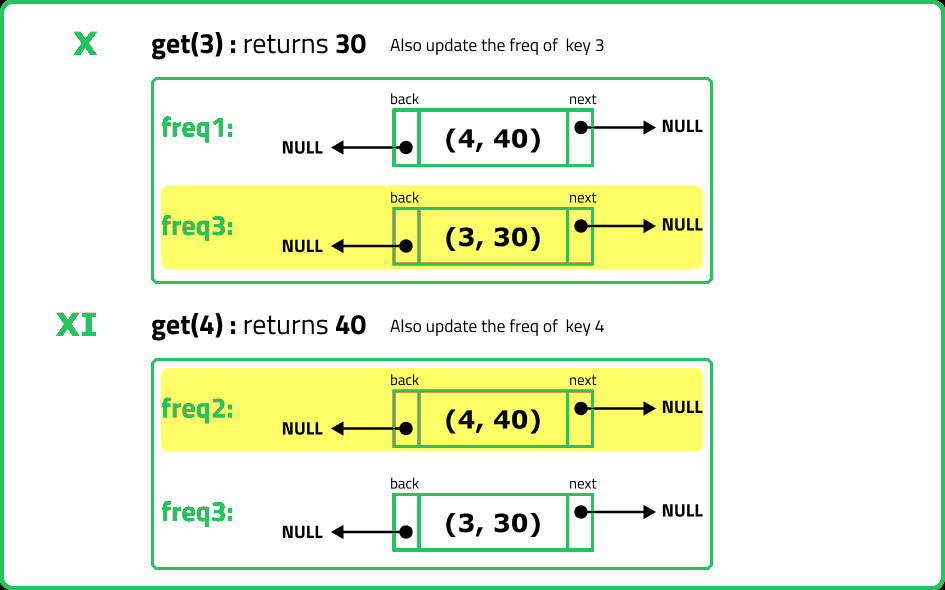
lfu.get(3); // return 3
// cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=[4,3], cnt(4)=2, cnt(3)=3
Input:
["LFUCache", "put", "put", "put", "put", "put", "get", "get", "get", "get", "get"]
[[3], [5, 7], [4, 6], [3, 5], [2, 4], [1, 3], [1], [2], [3], [4], [5]]
Output:
[null, null, null, null, null, null, 3, 4, 5, -1, -1]
Explanation:
// cnt(x) = the use counter for key x
// cache=[] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(3);
lfu.put(5, 7); // cache=[5], cnt(5)=1
lfu.put(4, 6); // cache=[4,5], cnt(4)=1, cnt(5)=1
lfu.put(3, 5); // cache=[3,4,5], cnt(3)=1, cnt(4)=1, cnt(5)=1
lfu.put(2, 4); // 5 is the LFU key because cnt(5)=1 is the smallest, invalidate 5.
// cache=[2,3,4], cnt(2)=1, cnt(3)=1, cnt(4)=1
lfu.put(1, 3); // 4 is the LFU key because cnt(4)=1 is the smallest, invalidate 4.
// cache=[1,2,3], cnt(1)=1, cnt(2)=1, cnt(3)=1
lfu.get(1); // return 3
// cache=[1,2,3], cnt(1)=2, cnt(2)=1, cnt(3)=1
lfu.get(2); // return 4
// cache=[2,1,3], cnt(1)=2, cnt(2)=2, cnt(3)=1
lfu.get(3); // return 5
// cache=[3,2,1], cnt(1)=2, cnt(2)=2, cnt(3)=2
lfu.get(4); // return -1 (not found)
lfu.get(5); // return -1 (not found)
Input:
["LFUCache", "put", "get", "put", "get", "get"]
[[1], [1, 10], [1], [2, 20], [1], [2]]
Constraints
- 1 <= capacity <= 103
- 0 <= key <= 104
- 0 <= value <= 105
- At most 105 calls will be made to get and put.
Hints
- A brute-force approach would iterate over all keys to find the least frequently used key, leading to O(n) time complexity, which is inefficient.
- Key-Value HashMap (cache) → Stores {key: (value, frequency)}. Frequency-List HashMap (freq_map) → Stores {frequency: OrderedDict(keys)}. Maintains order of access (LRU behavior) within the same frequency. A variable min_freq → Tracks the smallest frequency in freq_map (to identify LFU keys in O(1)).