Prime factorisation of a Number
Maths
Sieve of Eratosthenes
Hard
You are given an integer array queries of length n.
Return the prime factorization of each number in array queries in sorted order.
Examples:
Input : queries = [2, 3, 4, 5, 6]
Output : [ [2], [3], [2, 2], [5], [2, 3] ]
Explanation : The values 2, 3, 5 are itself prime numbers.
The prime factorization of 4 will be --> 2 * 2.
The prime factorization of 6 will be --> 2 * 3.
Input : queries = [7, 12, 18]
Output : [ [7], [2, 2, 3], [2, 3, 3] ]
Explanation : The value 7 itself is a prime number.
The prime factorization of 12 will be --> 2 * 2 * 3.
The prime factorization of 18 will be --> 2 * 3 * 3.
Input : queries = [15, 20]
Constraints
- 1 <= n <= 105
- 2 <= queries[i] <= 2*105
Hints
- A brute-force approach iterates through each number in queries and finds prime factors by checking divisibility from 2 to sqrt(num). This runs in O(n√m) (where m is the largest number in queries), which is inefficient for large numbers.
- "A better approach is the Modified Sieve of Eratosthenes, which: Precomputes the smallest prime factor (SPF) for all numbers up to the max(queries). Uses SPF to quickly factorize numbers in O(log m) time per number instead of checking divisibility repeatedly."
Company Tags
eBay
Splunk
Salesforce
Medtronic
Walmart
AMD
KPMG
Etsy
Activision Blizzard
Riot Games
Western Digital
Siemens Healthineers
Epic Games
Visa
Alibaba
Pinterest
Rakuten
Flipkart
Texas Instruments
HashiCorp
Seagate Technology
Swiggy
Boston Consulting Group
Morgan Stanley
Lyft
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
A naive approach to find the prime factorization of a given number is by dividing the number multiple times with the smallest prime number that divides it until the number becomes 1.
The prime factorisation for a number can be found in the following manner:
- The smallest prime number is 2. Thus, by repeatedly dividing the number by 2, all occurences of this prime factor are captured. This will reduce the number to an odd number.
- Once the number is odd, the smallest possible factors start from 3. Instead of checking every number, all the even numbers can be skipped since they are not prime (except 2, which is already handled).
- For each odd number up to the square root of the remaining number, if it is a factor, the number can be divided by this factorv epeatedly to capture all occurrences.
- Edge Case: After processing with all possible factors up to the square root, if there is any number left greater than 2, it must be a prime factor. This is because any composite number would have been divided down to smaller factors already.
Approach:
- Prime Factorization of a Single Number:
- A helper function is created to find the prime factors of a single number. It starts by repeatedly dividing the number by 2 to handle all factors of 2.
- Then, it iterates through all odd numbers from 3 up to the square root of the number, dividing the number by these odd numbers to find and store their factors.
- If the remaining number is greater than 2, it is also a prime factor and is added to the result.
- Processing the Queries:
- The main function takes an array of integers and applies the helper function to each element in the array.
- It stores the prime factors of each number in a 2D list where each sub-vector corresponds to the prime factors of a number in the input array.
- The computed result can be returned as the answer.
Dry Run:
Solution:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Helper function to find the prime
factorization of a number */
vector<int> primeFact(int n) {
// To store the result
vector<int> ans;
/* Keep dividing the number with
2 till it is possible */
while (n % 2 == 0) {
// Add 2 to result
ans.push_back(2);
// Update the number
n = n/2;
}
/* Start iterating from 3 skipping
one number (because n is now odd) */
for (int i=3; i <= sqrt(n); i += 2) {
// While i divides n
while (n % i == 0) {
// Store the number
ans.push_back(i);
// Update the number
n = n/i;
}
}
// Edge case
if (n > 2) ans.push_back(n);
// Return the result
return ans;
}
public:
/* Function to get the prime
factorization of all the number */
vector<vector<int>> primeFactors(vector<int>& queries){
// To store the answer
vector<vector<int>> ans;
// Iterate on each number in query
for(int i=0; i < queries.size(); i++) {
/* Function call to get the prime
factorization of current number */
ans.push_back(primeFact(queries[i]));
}
// Return the answer
return ans;
}
};
int main() {
vector<int> queries = {2, 3, 4, 5, 6};
/* Creating an instance of
Solution class */
Solution sol;
// Function call to get all primes till N
vector<vector<int>> ans = sol.primeFactors(queries);
cout << "The prime factorization of all the numbers is: " << endl;
for(int i=0; i < ans.size(); i++) {
cout << "For " << queries[i] << ": ";
for(int j=0; j < ans[i].size(); j++) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879
import java.util.*;
class Solution {
/* Helper function to find the prime
factorization of a number */
private List<Integer> primeFact(int n) {
// To store the result
List<Integer> ans = new ArrayList<>();
/* Keep dividing the number with
2 till it is possible */
while (n % 2 == 0) {
// Add 2 to result
ans.add(2);
// Update the number
n = n / 2;
}
/* Start iterating from 3 skipping
one number (because n is now odd) */
for (int i = 3; i <= Math.sqrt(n); i += 2) {
// While i divides n
while (n % i == 0) {
// Store the number
ans.add(i);
// Update the number
n = n / i;
}
}
// Edge case
if (n > 2) ans.add(n);
// Return the result
return ans;
}
/* Function to get the prime
factorization of all the number */
public List<List<Integer>> primeFactors(int[] queries) {
// To store the answer
List<List<Integer>> ans = new ArrayList<>();
// Iterate on each number in query
for (int i = 0; i < queries.length; i++) {
/* Function call to get the prime
factorization of current number */
ans.add(primeFact(queries[i]));
}
// Return the answer
return ans;
}
public static void main(String[] args) {
int[] queries = {2, 3, 4, 5, 6};
// Creating an instance of Solution class
Solution sol = new Solution();
// Function call to get all primes till N
List<List<Integer>> ans = sol.primeFactors(queries);
// Output
System.out.println("The prime factorization of all the numbers is: ");
for (int i = 0; i < ans.size(); i++) {
System.out.print("For " + queries[i] + ": ");
for (int j = 0; j < ans.get(i).size(); j++) {
System.out.print(ans.get(i).get(j) + " ");
}
System.out.println();
}
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
import math
class Solution:
# Helper function to find the prime
# factorization of a number
def primeFact(self, n):
# To store the result
ans = []
# Keep dividing the number
# with 2 till it is possible
while n % 2 == 0:
# Add 2 to result
ans.append(2)
# Update the number
n = n // 2
# Start iterating from 3 skipping
# one number (because n is now odd)
for i in range(3, int(math.sqrt(n)) + 1, 2):
# While i divides n
while n % i == 0:
# Store the number
ans.append(i)
# Update the number
n = n // i
# Edge case
if n > 2:
ans.append(n)
# Return the result
return ans
# Function to get the prime
# factorization of all the number
def primeFactors(self, queries):
# To store the answer
ans = []
# Iterate on each number in query
for i in range(len(queries)):
# Function call to get the prime
# factorization of current number
ans.append(self.primeFact(queries[i]))
# Return the answer
return ans
# Main code
if __name__ == "__main__":
queries = [2, 3, 4, 5, 6]
# Creating an instance of Solution class
sol = Solution()
# Function call to get all primes till N
ans = sol.primeFactors(queries)
print("The prime factorization of all the numbers is: ")
for i in range(len(ans)):
print(f"For {queries[i]}: ", end="")
for j in range(len(ans[i])):
print(ans[i][j], end=" ")
print()
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667
class Solution {
// Helper function to find the prime factorization of a number
primeFact(n) {
// To store the result
let ans = [];
// Keep dividing the number with 2 till it is possible
while (n % 2 === 0) {
// Add 2 to result
ans.push(2);
// Update the number
n = Math.floor(n / 2);
}
/* Start iterating from 3 skipping one
number (because n is now odd) */
for (let i = 3; i <= Math.sqrt(n); i += 2) {
// While i divides n
while (n % i === 0) {
// Store the number
ans.push(i);
// Update the number
n = Math.floor(n / i);
}
}
// Edge case
if (n > 2) ans.push(n);
// Return the result
return ans;
}
/* Function to get the prime
factorization of all the number */
primeFactors(queries) {
// To store the answer
let ans = [];
// Iterate on each number in query
for (let i = 0; i < queries.length; i++) {
/* Function call to get the prime
factorization of current number */
ans.push(this.primeFact(queries[i]));
}
// Return the answer
return ans;
}
}
// Main code
const queries = [2, 3, 4, 5, 6];
// Creating an instance of Solution class
const sol = new Solution();
// Function call to get all primes till N
const ans = sol.primeFactors(queries);
console.log("The prime factorization of all the numbers is: ");
for (let i = 0; i < ans.length; i++) {
console.log(`For ${queries[i]}: `, ans[i].join(" "));
}
Complexity Analysis:
Time Complexity: O(N x num1/2) (where N represents the number of queries and num represents the average of all the numbers in queries)
The PrimeFact(num) function has the time complexity of O(num1/2):
- The function divides the number by 2 until it is no longer divisible by 2. This loop runs at most log2num times.
- The function then iterates over all odd numbers from 3 to sqrt(num), and for each odd number i, it keeps dividing num by i until num is no longer divisible by i. The number of iterations here depends on the number of prime factors of num.
- In the worst case, the sum of the number of times each prime factor divides num is log2(num)
(since 2 x 3 x 5 x 7 x ... up to (num)1/2 covers all prime numbers).
Therefore, the time complexity of the primeFact(num) function is O(num1/2).
The PrimeFactorials(N) function has the time complexity of O(N x num1/2) because for all N numbers, PrimeFact(num) is called.
Space Complexity: O(N x log2(num))
Using a list to store the prime factorization of a number takes up O(log2(num)) space. Thus, for N numbers, the total space requirement is O(N x log2(num)).
Intuition:
The optimal solution aims to efficiently find the prime factorization of each number in a given array. Unlike the naive approach that repeatedly divides by potential factors, this solution precomputes the smallest prime factor for every number up to a maximum value using the Sieve of Eratosthenes. This optimization significantly reduces the time complexity when querying prime factorizations for multiple numbers.
The use of the Sieve of Eratosthenes allows for the precomputation of prime factors, making the prime factorization query for each number extremely fast.
Approach:
- An array, SPF, is initialized where each index represents a number, and the value at that index represents the smallest prime factor of the number. Initially, all values are set to 1.
- Sieve of Eratosthenes:
- Iterate through all numbers from 2 to MAX_N (100000 in this case).
- For each prime number found (i.e., numbers whose SPF value is still 1), mark its multiples with the prime number as their smallest prime factor.
- This process ensures that every number up to MAX_N has its smallest prime factor precomputed efficiently.
- Helper Function for Prime Factorization:
- Given a number, repeatedly divide it by its smallest prime factor (obtained from the SPF array) until the number is reduced to 1.
- Store each smallest prime factor during the division process.
- Handling Multiple Queries:
- The main function takes an array of integers and applies the helper function to each element.
- The prime factors of each number are stored in a 2D list, where each list corresponds to the prime factors of a number in the input array.
Dry Run:
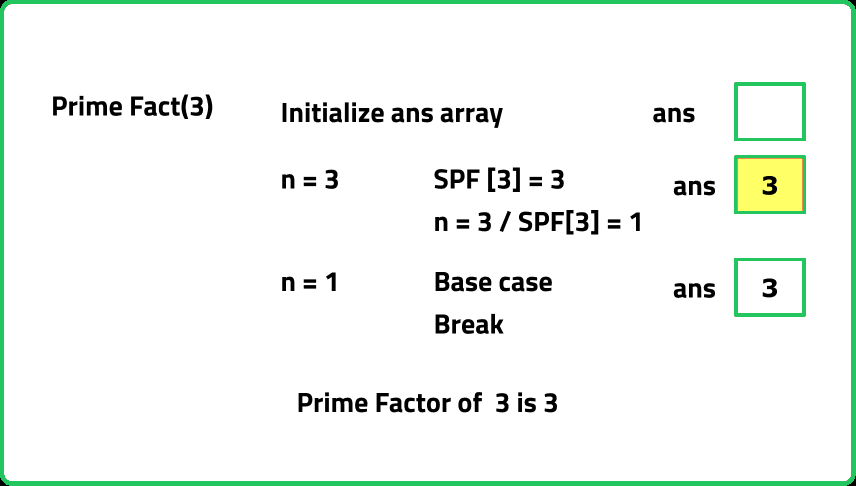
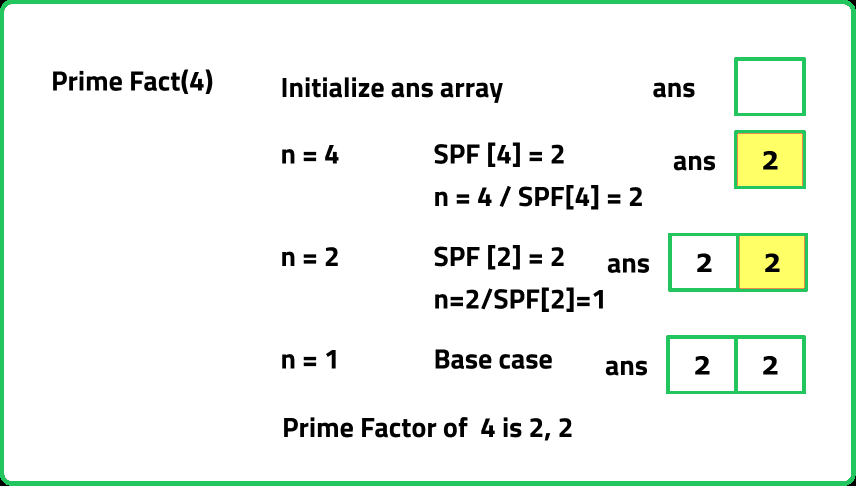
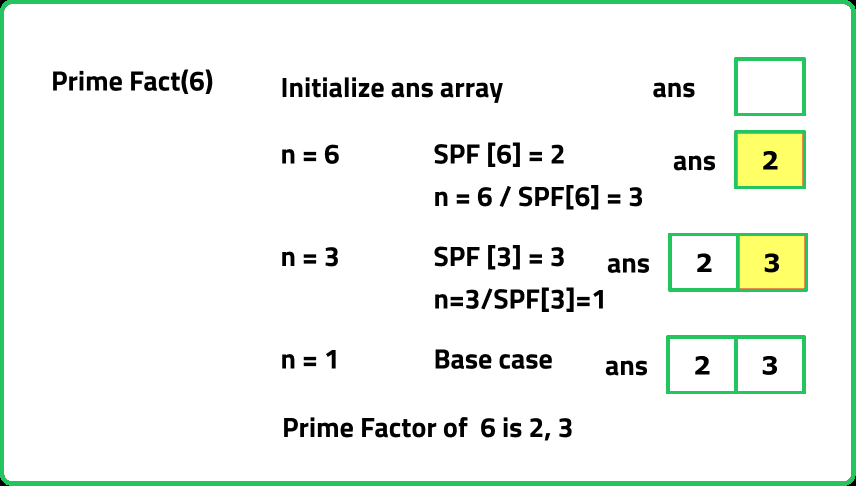
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108
#include <bits/stdc++.h>
using namespace std;
#define MAX_N 100000
/* To store the smallest prime factors for
all number with all nodes initially
having smallest prime factor as 1 */
vector<int> SPF(MAX_N + 1, 1);
class Solution{
private:
/* Function to precompute smallest prime
factor using sieve of eratosthenes */
void sieve() {
// Iterate on all the number
for (int i = 2; i <= MAX_N; i++) {
// If the number is a prime number
if (SPF[i] == 1) {
/* Mark all its multiples who have not
received their smallest prime factor yet*/
for (int j = i; j <= MAX_N; j += i) {
// If smallest prime factor not received yet
if (SPF[j]== 1) {
/* Store i as the smallest
prime factor for its multiple */
SPF[j] = i;
}
}
}
}
// Return
return;
}
/* Helper function to find the prime
factorization of a number */
vector<int> primeFact(int n) {
// To store the result
vector<int> ans;
// Until the number is not reduced to 1
while (n != 1) {
// Add the smallest prime factor to the list
ans.push_back(SPF[n]);
// Update the number
n = n / SPF[n];
}
// Return the result
return ans;
}
public:
/* Function to get the prime
factorization of all the number */
vector<vector<int>> primeFactors(vector<int>& queries){
/* Pre compute the smallest
possible factor for all numbers */
sieve();
// To store the answer
vector<vector<int>> ans;
// Iterate on each number in query
for(int i=0; i < queries.size(); i++) {
/* Function call to get the prime
factorization of current number */
ans.push_back(primeFact(queries[i]));
}
// Return the answer
return ans;
}
};
int main() {
vector<int> queries = {2, 3, 4, 5, 6};
/* Creating an instance of
Solution class */
Solution sol;
// Function call to get all primes till N
vector<vector<int>> ans = sol.primeFactors(queries);
cout << "The prime factorization of all the numbers is: " << endl;
for(int i=0; i < ans.size(); i++) {
cout << "For " << queries[i] << ": ";
for(int j=0; j < ans[i].size(); j++) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596
import java.util.*;
class Solution {
private static final int MAX_N = 100000;
/* To store the smallest prime factors for
all number with all nodes initially
having smallest prime factor as 1 */
private int[] SPF = new int[MAX_N + 1];
/* Constructor to initialize the smallest prime factor array */
public Solution() {
Arrays.fill(SPF, 1);
}
/* Function to precompute smallest prime
factor using sieve of eratosthenes */
private void sieve() {
// Iterate on all the number
for (int i = 2; i <= MAX_N; i++) {
// If the number is a prime number
if (SPF[i] == 1) {
/* Mark all its multiples who have not
received their smallest prime factor yet*/
for (int j = i; j <= MAX_N; j += i) {
// If smallest prime factor not received yet
if (SPF[j] == 1) {
/* Store i as the smallest
prime factor for its multiple */
SPF[j] = i;
}
}
}
}
}
/* Helper function to find the prime
factorization of a number */
private List<Integer> primeFact(int n) {
// To store the result
List<Integer> ans = new ArrayList<>();
// Until the number is not reduced to 1
while (n != 1) {
// Add the smallest prime factor to the list
ans.add(SPF[n]);
// Update the number
n = n / SPF[n];
}
// Return the result
return ans;
}
/* Function to get the prime
factorization of all the number */
public List<List<Integer>> primeFactors(int[] queries) {
/* Precompute the smallest
possible factor for all numbers */
sieve();
// To store the answer
List<List<Integer>> ans = new ArrayList<>();
// Iterate on each number in query
for (int query : queries) {
/* Function call to get the prime
factorization of current number */
ans.add(primeFact(query));
}
// Return the answer
return ans;
}
public static void main(String[] args) {
int[] queries = {2, 3, 4, 5, 6};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
// Function call to get all primes till N
List<List<Integer>> ans = sol.primeFactors(queries);
System.out.println("The prime factorization of all the numbers is: ");
for (int i = 0; i < ans.size(); i++) {
System.out.print("For " + queries[i] + ": ");
for (int factor : ans.get(i)) {
System.out.print(factor + " ");
}
System.out.println();
}
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
MAX_N = 100000
# To store the smallest prime factors for
# all number with all nodes initially
# having smallest prime factor as 1
SPF = [1] * (MAX_N + 1)
class Solution:
def __init__(self):
self.sieve()
# Function to precompute smallest prime
# factor using sieve of eratosthenes
def sieve(self):
# Iterate on all the number
for i in range(2, MAX_N + 1):
# If the number is a prime number
if SPF[i] == 1:
# Mark all its multiples who have not
# received their smallest prime factor yet
for j in range(i, MAX_N + 1, i):
# If smallest prime factor not received yet
if SPF[j] == 1:
# Store i as the smallest
# prime factor for its multiple
SPF[j] = i
# Helper function to find the prime
# factorization of a number
def primeFact(self, n):
# To store the result
ans = []
# Until the number is not reduced to 1
while n != 1:
# Add the smallest prime factor to the list
ans.append(SPF[n])
# Update the number
n = n // SPF[n]
# Return the result
return ans
# Function to get the prime
# factorization of all the number
def primeFactors(self, queries):
# To store the answer
ans = []
# Iterate on each number in query
for query in queries:
# Function call to get the prime
# factorization of current number
ans.append(self.primeFact(query))
# Return the answer
return ans
if __name__ == "__main__":
queries = [2, 3, 4, 5, 6]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to get all primes till N
ans = sol.primeFactors(queries)
print("The prime factorization of all the numbers is: ")
for i in range(len(ans)):
print(f"For {queries[i]}: ", end="")
for factor in ans[i]:
print(factor, end=" ")
print()
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586
const MAX_N = 100000;
/* To store the smallest prime factors for
all number with all nodes initially
having smallest prime factor as 1 */
const SPF = new Array(MAX_N + 1).fill(1);
class Solution {
constructor() {
this.sieve();
}
/* Function to precompute smallest prime
factor using sieve of eratosthenes */
sieve() {
// Iterate on all the number
for (let i = 2; i <= MAX_N; i++) {
// If the number is a prime number
if (SPF[i] === 1) {
/* Mark all its multiples who have not
received their smallest prime factor yet */
for (let j = i; j <= MAX_N; j += i) {
// If smallest prime factor not received yet
if (SPF[j] === 1) {
/* Store i as the smallest prime
factor for its multiple */
SPF[j] = i;
}
}
}
}
}
/* Helper function to find the prime
factorization of a number */
primeFact(n) {
// To store the result
const ans = [];
// Until the number is not reduced to 1
while (n !== 1) {
// Add the smallest prime factor to the list
ans.push(SPF[n]);
// Update the number
n = n / SPF[n];
}
// Return the result
return ans;
}
/* Function to get the prime
factorization of all the number */
primeFactors(queries) {
// To store the answer
const ans = [];
// Iterate on each number in query
for (let i = 0; i < queries.length; i++) {
/* Function call to get the prime
factorization of current number */
ans.push(this.primeFact(queries[i]));
}
// Return the answer
return ans;
}
}
const queries = [2, 3, 4, 5, 6];
/* Creating an instance of
Solution class */
const sol = new Solution();
// Function call to get all primes till N
const ans = sol.primeFactors(queries);
console.log("The prime factorization of all the numbers is: ");
for (let i = 0; i < ans.length; i++) {
console.log(`For ${queries[i]}: ${ans[i].join(" ")}`);
}
Complexity Analysis:
Time Complexity: O(max_N x log(log(max_N))) + O(N x log(num)) (where N represent the number of queries, num represents the average number in the queries and max_N = 105)
- The Sieve of Eratosthenes takes O(max_N x log(log(max_N))) to pre compute the smallest prime factor for all numbers till max_N.
- In the worst case, finding the prime factors of a number num takes O(log(num)) time since the number is divided by its smallest prime factor until it becomes 1. For N queries, the total time taken will be O(N x log(num)).
Space Complexity: O(max_N) + O(N x log(num))
The SPF array takes O(max_N) space and the space taken by list to store the result is O(N x log(num)).
Frequently Occurring Doubts
Q: Why use SPF instead of brute-force division?
A: The Smallest Prime Factor (SPF) array allows factorization in O(log m) per number by iteratively dividing by precomputed smallest primes. Brute-force checking requires O(√m) per number, which is slower.
Q: Can we use the Sieve of Eratosthenes directly for factorization?
A: Standard Sieve finds primes, but Modified Sieve precomputes SPF, allowing faster factorization.
Interview Followup Questions
Q: How does this compare to Pollard’s Rho algorithm for factorization?
A: Pollard’s Rho is used for extremely large numbers (e.g., 10¹⁸+), whereas SPF is best for numbers ≤ 10⁶.
Q: How would you modify this approach to return factors with their exponents (e.g., {2:3, 5:1} for 40)?
A: Instead of storing factors in a list, use a dictionary to count occurrences.
Notes
Code
✅ Testcase
Input: {'queries': '[2, 3, 4, 5, 6]'}
Expected:
2
3
2 2
5
2 3
2
3
2 2
5
2 3
Actual: -
Time: -
sec
Status: Waiting
Input: {'queries': '[7, 12, 18]'}
Expected:
7
2 2 3
2 3 3
7
2 2 3
2 3 3
Actual: -
Time: -
sec
Status: Waiting
Input: {'queries': '[11, 13, 15, 17]'}
Expected:
11
13
3 5
17
11
13
3 5
17
Actual: -
Time: -
sec
Status: Waiting