Count of prime numbers till N

Beginner Problems Basic Maths Easy

Prime number generation and recognition is an important concept in cryptographic algorithms, which serve as a basis for secure communication in the digital world
For example, RSA algorithm, which is widely used for secure data transmission, is based on the principle of factoring large prime numbers
The difficulty in factoring the product of two large prime numbers ensures that RSA is secure
Therefore, a function that can efficiently generate or identify prime numbers can contribute to the efficiency and strength of these algorithms

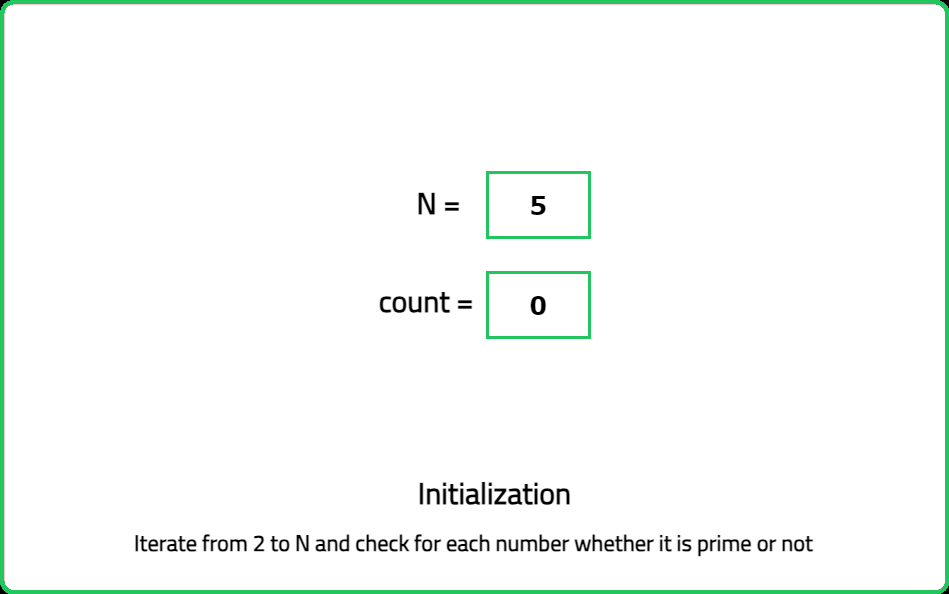
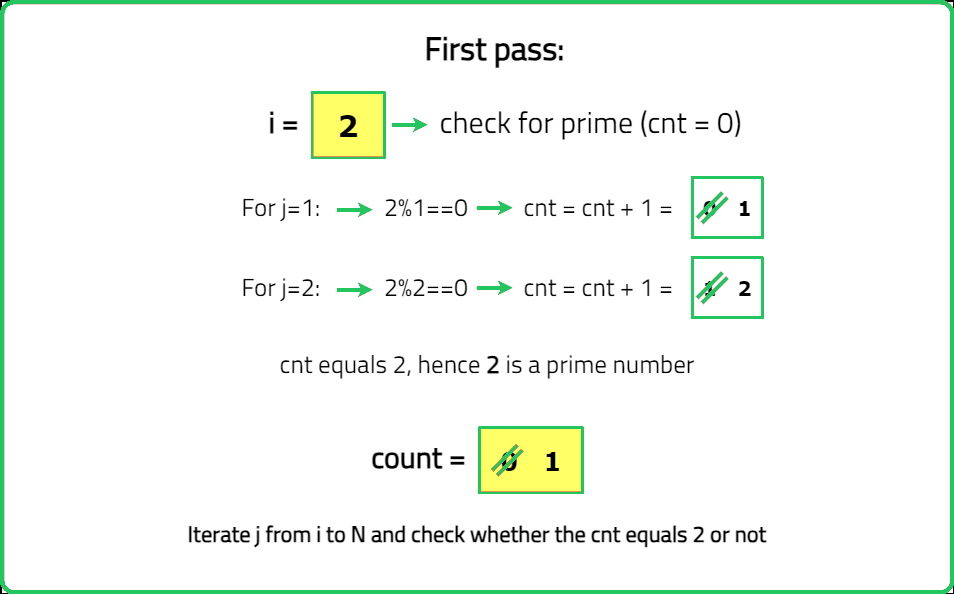
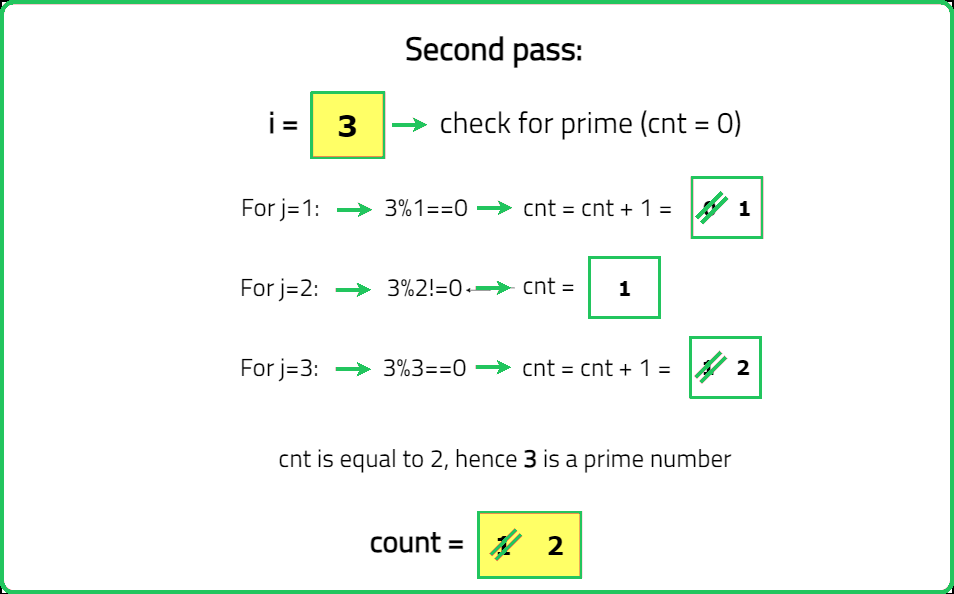
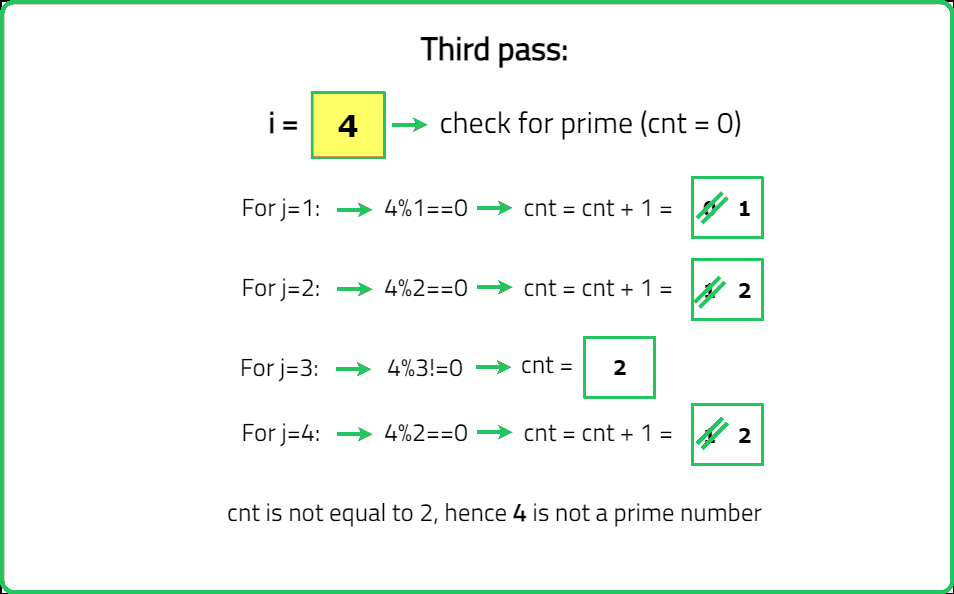
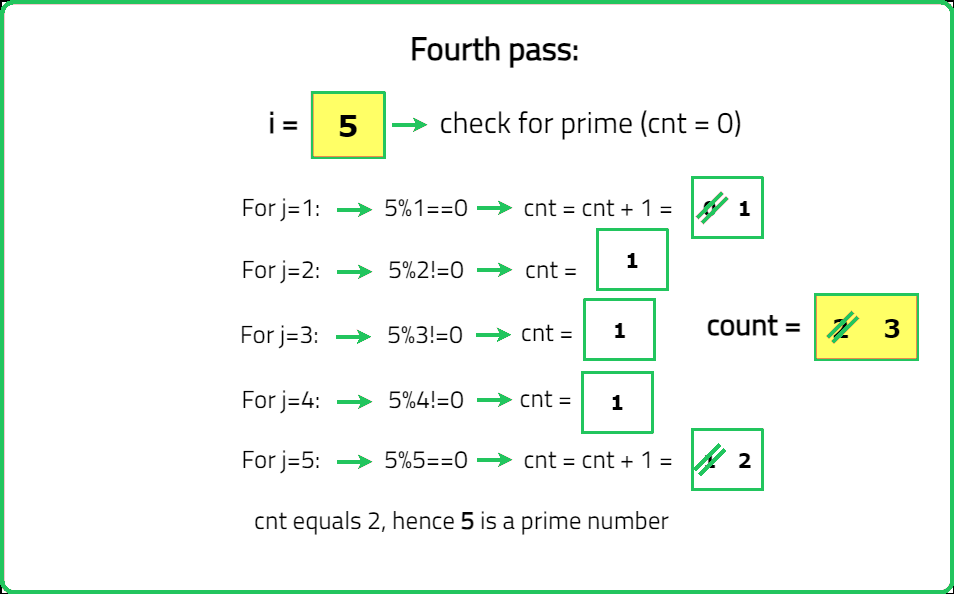
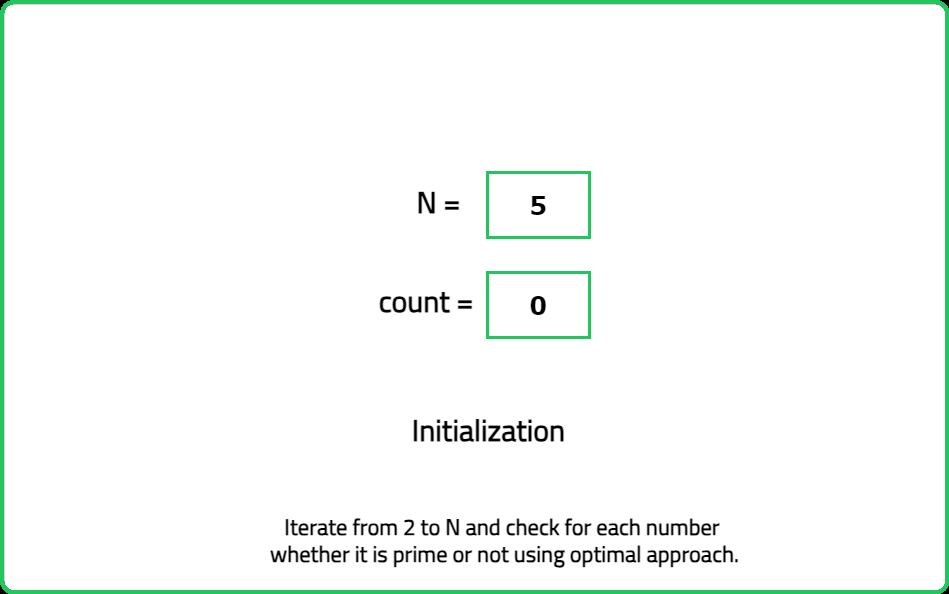
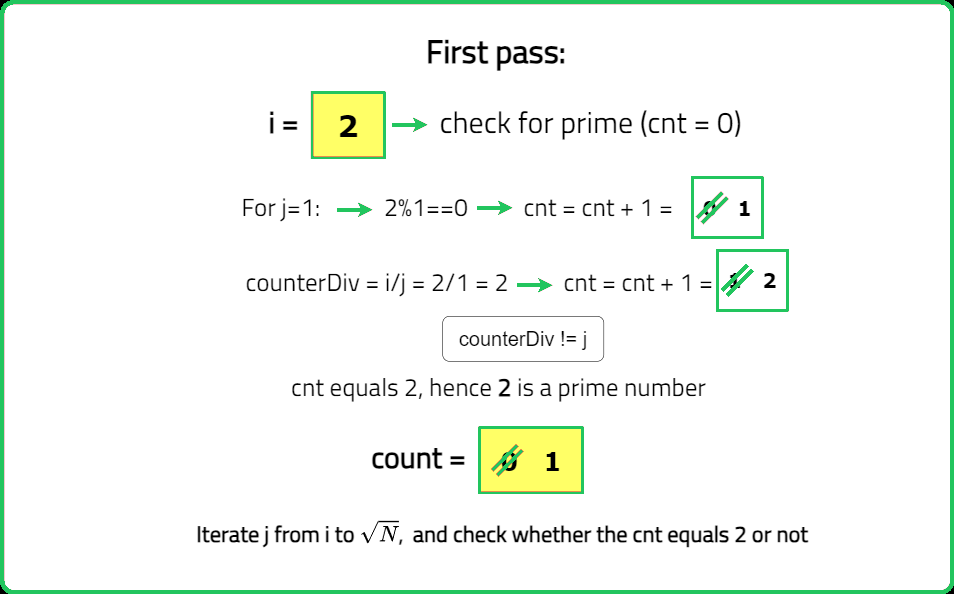
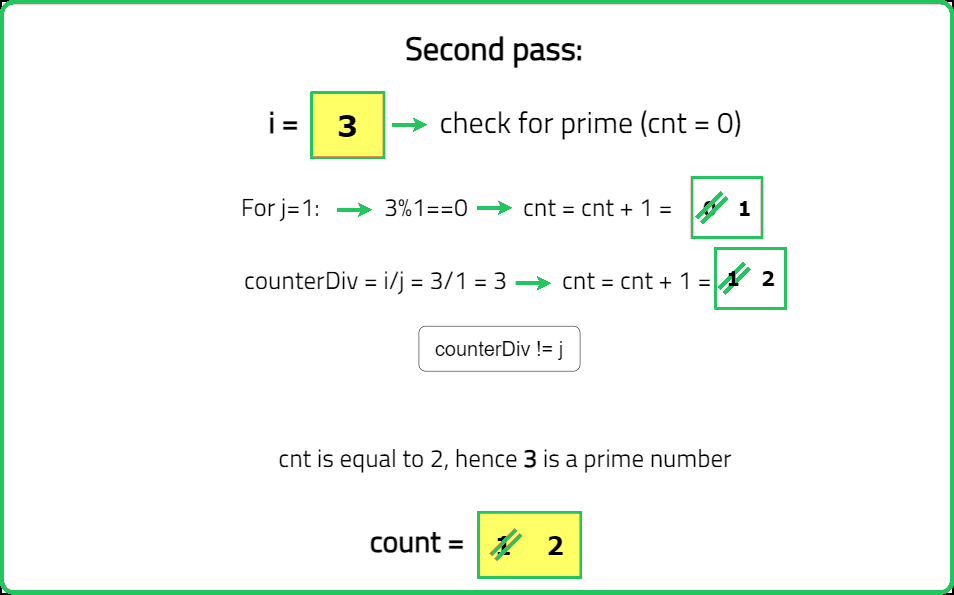
You are given an integer n. You need to find out the number of prime numbers in the range [1, n] (inclusive). Return the number of prime numbers in the range.

A prime number is a number which has no divisors except, 1 and itself.

Examples:

Input: n = 6

Output: 3

Explanation: Prime numbers in the range [1, 6] are 2, 3, 5.

Input: n = 10

Output: 4

Explanation: Prime numbers in the range [1, 10] are 2, 3, 5, 7.

Input: n = 20

Constraints

2 <= n <= 1000

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

              document.body.innerHTML = '';
              const iframeHTML = `
                <div style="padding-top:56.25%;position:relative;">
                  <iframe 
                    src="https://app.tpstreams.com/embed/atsjxr/6pMpS4ZqRGf/?access_token=33e345b1-9f22-4382-8c5c-7e49a75d8027" 
                    style="border:0;max-width:100%;position:absolute;top:0;left:0;height:100%;width:100%;" 
                    allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" 
                    allowfullscreen="" 
                    frameborder="0">
                  </iframe>
                </div>
              `;
              document.body.innerHTML = iframeHTML;
              
              const script = document.createElement('script');
              script.src = 'https://static.testpress.in/static/js/player.js';
              document.head.appendChild(script);
              
              script.onload = () => {
                const iframe = document.querySelector('iframe');
                const player = new Testpress.Player(iframe);
              
                player.loaded().then(() => {
                  console.log('Player is ready now');
                });
              
                player.on('play', () => {
                  console.log('Played the video');
                });
              };

Intuition:

A naive approach to count prime numbers till N, is to check every number starting from 1 till N for prime. Keep a counter to store the count. If the number is prime, increment the counter. Once all the numbers are checked, the counter stores the required count.

Approach:

Initialize a counter to store the count of prime numbers.
Iterate from 2 to n, and check the current value for prime (using the brute way). If found prime, increment the counter by 1.
After the iterations are over, the counter stores the required result.

Dry Run:

1 / 6

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to find whether the
    number is prime or not */
    bool isPrime(int n) {
        
        /* Variable to store the 
        count of divisors of n */
        int count = 0;
        
        // Loop from 1 to n
        for (int i = 1; i <= n; ++i) {
            
            // Check if i is a divisor
            if (n % i == 0) {
                // Increment count
                count = count + 1;
            }
        }
        
        // If count is 2, n is prime
        if (count == 2) return true;
        // Else not prime
        return false;
    }
    
public:
    /* Function to find count
    of primes till n */
    int primeUptoN(int n) {
        
        // Variable to store count
        int count = 0;
        
        // Iterate from 1 to n
        for (int i = 2; i <= n; i++) {
            
            // Check if i is prime
            if (isPrime(i)) count++;
        }
        
        // Return the count
        return count;
    }
};

int main() {
    int n = 6;
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to get 
    count of all primes till n */
    int ans = sol.primeUptoN(n);
    
    cout << "The count of primes till " << n << " is: " << ans;
    
    return 0;
}
class Solution {
    /* Function to find whether the
    number is prime or not */
    private boolean isPrime(int n) {
        
        /* Variable to store the 
        count of divisors of n */
        int count = 0;
        
        // Loop from 1 to n
        for (int i = 1; i <= n; ++i) {
            
            // Check if i is a divisor
            if (n % i == 0) {
                // Increment count
                count = count + 1;
            }
        }
        
        // If count is 2, n is prime
        if (count == 2) return true;
        // Else not prime
        return false;
    }
    
    /* Function to find count
    of primes till n */
    public int primeUptoN(int n) {
        
        // Variable to store count
        int count = 0;
        
        // Iterate from 1 to n
        for (int i = 2; i <= n; i++) {
            
            // Check if i is prime
            if (isPrime(i)) count++;
        }
        
        // Return the count
        return count;
    }

    public static void main(String[] args) {
        int n = 6;
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution(); 
        
        /* Function call to get 
        count of all primes till n */
        int ans = sol.primeUptoN(n);
        
        System.out.println("The count of primes till " + n + " is: " + ans);
    }
}
class Solution:
    # Function to find whether the
    # number is prime or not
    def isPrime(self, n):
        
        # Variable to store the 
        # count of divisors of n
        count = 0
        
        # Loop from 1 to n
        for i in range(1, n + 1):
            
            # Check if i is a divisor
            if n % i == 0:
                # Increment count
                count = count + 1
        
        # If count is 2, n is prime
        if count == 2:
            return True
        # Else not prime
        return False
    
    # Function to find count
    # of primes till n
    def primeUptoN(self, n):
        
        # Variable to store count
        count = 0
        
        # Iterate from 1 to n
        for i in range(2, n + 1):
            
            # Check if i is prime
            if self.isPrime(i):
                count += 1
        
        # Return the count
        return count

# Input number
n = 6

# Creating an instance of Solution class
sol = Solution()

# Function call to get count of all primes till n
ans = sol.primeUptoN(n)

print("The count of primes till", n, "is:", ans)
class Solution {
    // Function to find whether the
    // number is prime or not
    isPrime(n) {
        
        // Variable to store the 
        // count of divisors of n
        let count = 0;
        
        // Loop from 1 to n
        for (let i = 1; i <= n; ++i) {
            
            // Check if i is a divisor
            if (n % i === 0) {
                // Increment count
                count = count + 1;
            }
        }
        
        // If count is 2, n is prime
        if (count === 2) return true;
        // Else not prime
        return false;
    }
    
    // Function to find count
    // of primes till n
    primeUptoN(n) {
        
        // Variable to store count
        let count = 0;
        
        // Iterate from 1 to n
        for (let i = 2; i <= n; i++) {
            
            // Check if i is prime
            if (this.isPrime(i)) count++;
        }
        
        // Return the count
        return count;
    }
}

// Input number
let n = 6;

// Creating an instance of Solution class
let sol = new Solution();

// Function call to get count of all primes till n
let ans = sol.primeUptoN(n);

console.log("The count of primes till " + n + " is: " + ans);

Complexity Analysis:

Time Complexity: O(N²) – Checking all numbers from 1 to n for prime and checking if a number is prime or not will take O(n) TC.

Space Complexity: O(1) – Using a couple of variables i.e., constant space.

              document.body.innerHTML = '';
              const iframeHTML = `
                <div style="padding-top:56.25%;position:relative;">
                  <iframe 
                    src="https://app.tpstreams.com/embed/atsjxr/6pMpS4ZqRGf/?access_token=33e345b1-9f22-4382-8c5c-7e49a75d8027" 
                    style="border:0;max-width:100%;position:absolute;top:0;left:0;height:100%;width:100%;" 
                    allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" 
                    allowfullscreen="" 
                    frameborder="0">
                  </iframe>
                </div>
              `;
              document.body.innerHTML = iframeHTML;
              
              const script = document.createElement('script');
              script.src = 'https://static.testpress.in/static/js/player.js';
              document.head.appendChild(script);
              
              script.onload = () => {
                const iframe = document.querySelector('iframe');
                const player = new Testpress.Player(iframe);
              
                player.loaded().then(() => {
                  console.log('Player is ready now');
                });
              
                player.on('play', () => {
                  console.log('Played the video');
                });
              };

Intuition:

The previous approach can be optimized by improving the complexity of the function to find whether a number is prime or not.

Approach:

Initialize a counter to store the count of prime numbers.
Iterate from 2 to n, and check the current value for prime (using the optimal way). If found prime, increment the counter by 1.
After the iterations are over, the counter stores the required result.

Dry Run:

1 / 6

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to find whether the
    number is prime or not */
    bool isPrime(int n) {
        
        /* Variable to store the 
        count of divisors of n */
        int count = 0;
        
        // Loop from 1 to square root of n
        for(int i = 1; i <= sqrt(n); ++i) {
            
            // Check if i is a divisor
            if(n % i == 0) {
                // Increment count
                count = count + 1;
                
                /* Check if counterpart divisor
                is different from original divisor */
                if(n % i != i) {
                    
                    // Increment count
                    count = count + 1;
                }
            }
        }
        
        // If count is 2, n is prime
        if(count == 2) return true;
        // Else not prime
        return false;
    }
    
public:
    /* Function to find count
    of primes till n */
    int primeUptoN(int n) {
        
        // Variable to store count
        int count = 0;
        
        // Iterate from 1 to n
        for (int i = 2; i <= n; i++) {
            
            // Check if i is prime
            if (isPrime(i)) count++;
        }
        
        // Return the count
        return count;
    }
};

int main() {
    int n = 6;
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to get 
    count of all primes till n */
    int ans = sol.primeUptoN(n);
    
    cout << "The count of primes till " << n << " is: " << ans;
    
    return 0;
}
class Solution {
    // Function to find whether the number is prime or not
    private boolean isPrime(int n) {
        // Variable to store the count of divisors of n
        int count = 0;
        
        // Loop from 1 to square root of n
        for (int i = 1; i <= Math.sqrt(n); ++i) {
            // Check if i is a divisor
            if (n % i == 0) {
                // Increment count
                count = count + 1;
                
                /* Check if counterpart divisor is 
                different from original divisor */
                if (n / i != i) {
                    // Increment count
                    count = count + 1;
                }
            }
        }
        
        // If count is 2, n is prime
        return count == 2;
    }
    
    // Function to find count of primes till n
    public int primeUptoN(int n) {
        // Variable to store count
        int count = 0;
        
        // Iterate from 1 to n
        for (int i = 2; i <= n; i++) {
            // Check if i is prime
            if (isPrime(i)) count++;
        }
        
        // Return the count
        return count;
    }
    
    public static void main(String[] args) {
        int n = 6;
        
        // Creating an instance of Solution class
        Solution sol = new Solution();
        
        /* Function call to get count 
        of all primes till n */
        int ans = sol.primeUptoN(n);
        
        System.out.println("The count of primes till " + n + " is: " + ans);
    }
}
import math

class Solution:
    # Function to find whether 
    # the number is prime or not
    def isPrime(self, n):
        # Variable to store the count 
        # of divisors of n
        count = 0
        
        # Loop from 1 to square root of n
        for i in range(1, int(math.sqrt(n)) + 1):
            # Check if i is a divisor
            if n % i == 0:
                # Increment count
                count += 1
                
                # Check if counterpart divisor is 
                # different from original divisor
                if n // i != i:
                    # Increment count
                    count += 1
        
        # If count is 2, n is prime
        return count == 2
    
    # Function to find count of primes till n
    def primeUptoN(self, n):
        # Variable to store count
        count = 0
        
        # Iterate from 1 to n
        for i in range(2, n + 1):
            # Check if i is prime
            if self.isPrime(i):
                count += 1
        
        # Return the count
        return count

if __name__ == "__main__":
    n = 6
    
    # Creating an instance of Solution class
    sol = Solution()
    
    # Function call to get count of all primes till n
    ans = sol.primeUptoN(n)
    
    print(f"The count of primes till {n} is: {ans}")
class Solution {
    /* Function to find whether the 
     number is prime or not */
    isPrime(n) {
        /* Variable to store the 
        count of divisors of n */
        let count = 0;
        
        // Loop from 1 to square root of n
        for (let i = 1; i <= Math.sqrt(n); ++i) {
            // Check if i is a divisor
            if (n % i === 0) {
                // Increment count
                count = count + 1;
                
                /* Check if counterpart divisor is 
                different from original divisor */
                if (n / i !== i) {
                    // Increment count
                    count = count + 1;
                }
            }
        }
        
        // If count is 2, n is prime
        return count === 2;
    }
    
    // Function to find count of primes till n
    primeUptoN(n) {
        // Variable to store count
        let count = 0;
        
        // Iterate from 1 to n
        for (let i = 2; i <= n; i++) {
            // Check if i is prime
            if (this.isPrime(i)) count++;
        }
        
        // Return the count
        return count;
    }
}

// Input number
let n = 6;

// Creating an instance of Solution class
let sol = new Solution();

// Function call to get count of all primes till n
let ans = sol.primeUptoN(n);

console.log("The count of primes till " + n + " is: " + ans);

Complexity Analysis:

Time Complexity: O(N^3/2) – Checking all numbers from 1 to N for prime and checking if a number is prime or not will take O(N^1/2) TC.

Space Complexity: O(1) – Using a couple of variables i.e., constant space.

Code

Problem List

Count of prime numbers till N

Examples:

Constraints

Company Tags

Editorial

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Notes

Code