Fibonacci Number

Beginner Problems Basic Recursion Easy

The Fibonacci sequence is a fundamental concept in computer science and finds use in several real-world applications
One fascinating example lies in agile project management, specifically Scrum
Team members use Fibonacci numbers to estimate the complexity or effort required for tasks
This system, known as Fibonacci estimation, is based on the theory that it’s harder to estimate bigger tasks with precision, so Fibonacci's ever-increasing gap between numbers reflects this uncertainty

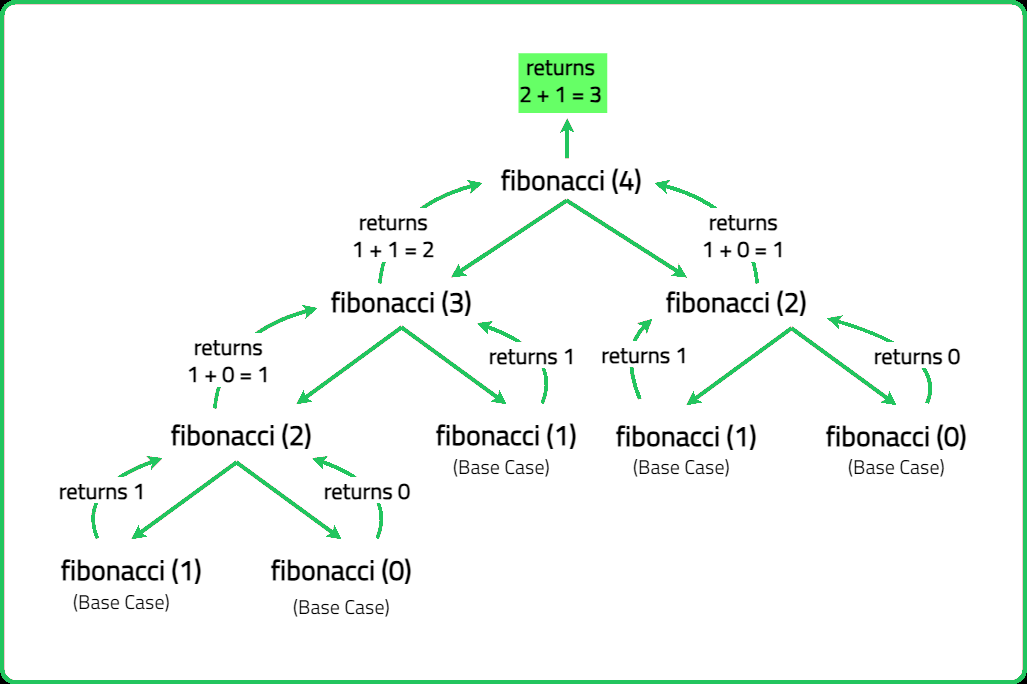
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

Given n, calculate F(n).

Examples:

Input : n = 2

Output : 1

Explanation : F(2) = F(1) + F(0) => 1 + 0 => 1.

Input : n = 3

Output : 2

Explanation : F(3) = F(2) + F(1) => 1 + 1 => 2.

Input : n = 6

Constraints

0 <= n <= 19

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

Intuition

This problem can be broken into smaller problems using recursion by calculating Fibonacci numbers for previous positions and combining these results to find the Fibonacci number for the desired position . To find the Fibonacci number at a certain position, start with two base cases: F(0) = 0 and F(1) = 1. For any position greater than 1, the Fibonacci number can be found by adding the two preceding Fibonacci numbers: F(n) = F(n-1) + F(n-2).

Approach

Define a recursive function that returns 0 if n is 0, and 1 if n is 1 (base cases).
For n > 1, return the sum of the Fibonacci numbers for n-1 and n-2 (recursive case).
Call the function with the desired n to get the Fibonacci number.

Dry Run

Solution

class Solution {
public:
    int fib(int n) {
        // Base cases: F(0) = 0, F(1) = 1
        if (n == 0) return 0;
        if (n == 1) return 1;
        // Recursive case: F(n) = F(n-1) + F(n-2)
        return fib(n - 1) + fib(n - 2);
    }
};

int main() {
    Solution solution;
    int n = 5; // Example input
    cout << "Fibonacci number at position " << n << " is " << solution.fibonacci(n) << endl;
    return 0;
}
class Solution {
    public int fib(int n) {
        // Base cases: F(0) = 0, F(1) = 1
        if (n == 0) return 0;
        if (n == 1) return 1;
        // Recursive case: F(n) = F(n-1) + F(n-2)
        return fib(n - 1) + fib(n - 2);
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int n = 5; // Example input
        System.out.println("Fibonacci number at position " + n + " is " + solution.fibonacci(n));
    }
}
class Solution:
    def fib(self, n):
        # Base cases: F(0) = 0, F(1) = 1
        if n == 0:
            return 0
        elif n == 1:
            return 1
        # Recursive case: F(n) = F(n-1) + F(n-2)
        return self.fib(n - 1) + self.fib(n - 2)

if __name__ == "__main__":
    solution = Solution()
    n = 5  # Example input
    print(f"Fibonacci number at position {n} is {solution.fibonacci(n)}")
class Solution {
    fib(n) {
        // Base cases: F(0) = 0, F(1) = 1
        if (n === 0) return 0;
        if (n === 1) return 1;
        // Recursive case: F(n) = F(n-1) + F(n-2)
        return this.fib(n - 1) + this.fib(n - 2);
    }
}

const solution = new Solution();
const n = 5; // Example input
console.log(`Fibonacci number at position ${n} is ${solution.fibonacci(n)}`);

Complexity Analysis

Time Complexity O(2^N) — Each function call makes two more calls (for n-1 and n-2), resulting in an exponential growth in the number of calls.

Space Complexity O(N)— The call stack grows with each recursive call, using N stack frames, so the space complexity is proportional to the recursion depth.

Code

Problem List