0 and 1 Knapsack
Dynamic Programming
DP on subsequences
Hard
Given two integer arrays, val and wt, each of size N, which represent the values and weights of N items respectively, and an integer W representing the maximum capacity of a knapsack, determine the maximum value achievable by selecting a subset of the items such that the total weight of the selected items does not exceed the knapsack capacity W.
Each item can either be picked in its entirety or not picked at all (0-1 property). The goal is to maximize the sum of the values of the selected items while keeping the total weight within the knapsack's capacity.
Examples:
Input: val = [60, 100, 120], wt = [10, 20, 30], W = 50
Output: 220
Explanation: Select items with weights 20 and 30 for a total value of 100 + 120 = 220.
Input: val = [10, 40, 30, 50], wt = [5, 4, 6, 3], W = 10
Output: 90
Explanation: Select items with weights 4 and 3 for a total value of 40 + 50 = 90.
Input: val = [20, 5, 10, 40, 15, 25], wt = [1, 2, 3, 8, 7, 4], W = 10
Constraints
- 1 ≤ N ≤ 500
- 1 ≤ W ≤ 1000
- 1 ≤ wt[i] ≤ 500
- 1 ≤ val[i] ≤ 500
Hints
- "Define dp[i][w] as the maximum value achievable using the first i items with a knapsack capacity of w. the recurrence relation is: dp[i][w]=max(dp[i−1][w],dp[i−1][w−wt[i]]+val[i])(if wt[i]≤w) "
- "Instead of a full dp[n][W] table, we can use a 1D array (dp[W]) and iterate backward (right to left): dp[w]=max(dp[w],dp[w−wt[i]]+val[i]) We iterate from W down to wt[i] to prevent overwriting values."
Company Tags
Medtronic
Ubisoft
Nutanix
Cerner
Walmart
Bungie
Cloudflare
Western Digital
Qualcomm
HCL Technologies
Etsy
Unity Technologies
Philips Healthcare
Visa
Ernst & Young
Rakuten
Instacart
Morgan Stanley
Shopify
Wayfair
Stripe
Roblox
Siemens Healthineers
Broadcom
Pinterest
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Why a Greedy Solution will not work:
As the question is asking for maximum value, the first approach that comes to our mind is greedy. A greedy solution will fail in this problem because there is no ‘uniformity’ in data. While selecting a local better choice we may choose an item that will in long term give less value. So we will solve this problem using recursion.
Steps to form the recursive solution:
- Express the problem in terms of indexes:We are given ‘n’ items. Their weight is represented by the ‘wt’ array and value by the ‘val’ array. So clearly one parameter will be ‘ind’, i.e index up to which the array items are being considered. There is one more parameter 'W', the capacity of the knapsack to decide whether we can pick an array item or not in the knapsack.
So initially, we need to find f(n-1, W) where W is the overall capacity given to us. f(n-1, W) gives the maximum value of items that we can get from index 0 to n-1 with capacity W of the knapsack.
- Try out all possible choices at a given index:We need to generate all the subsequences. We will use the pick/non-pick technique. There will be two choices:
- Return the maximum of take and notTake: As we have to return the maximum amount of value, we will return the maximum of take and notTake as our answer.
- Base Case: If ind==0, it means we are at the first item, so in that case we will check whether this item’s weight is less than or equal to the current capacity W, if it is, we simply return its value (val[0]) else we return 0.
Exclude the current element from the subsequence: First try to find a subsequence without considering the current index item. If we exclude the current item, the capacity of the bag will not be affected and the value added will be 0 for the current item. So we will call the recursive function f(ind-1,W),
Include the current element in the subsequence: Try to find a subsequence by considering the current item to the knapsack. As we have included the item, the capacity of the knapsack will be updated to (W-wt[ind]) and the current item’s value (val[ind] will also be added to the further recursive call answer. We will make a recursive call to f(ind-1, W- wt[ind]).
Note: We will consider the current item in the subsequence only when the current element’s weight is less than or equal to the capacity ‘W’ of the knapsack, if it isn’t we will not be considering it.
1234
f(ind, W){
notTake = 0 + f(ind-1, W)
take = INT_MIN
if(wt[ind] <= W)
take = val[ind] + f(ind-1, W-wt[ind])
}1234
f(ind, W){
notTake = 0 + f(ind-1, W)
take = INT_MIN
if(wt[ind] <= W)
take = val[ind] + f(ind-1, W-wt[ind])
return max(take, notTake)
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
// Function to solve 0/1 Knapsack problem using memoization
int func(vector<int>& wt, vector<int>& val, int ind, int W) {
/* Base case: If there are no items left
or the knapsack has no capacity, return 0*/
if (ind == 0 || W == 0) {
return 0;
}
/* Calculate the maximum value by either
excluding the current item or including it*/
int notTaken = func(wt, val, ind - 1, W);
int taken = 0;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= W) {
taken = val[ind] + func(wt, val, ind - 1, W - wt[ind]);
}
// Return the result
return max(notTaken, taken);
}
public:
// Function to solve the 0/1 Knapsack problem
int knapsack01(vector<int>& wt, vector<int>& val, int n, int W) {
return func(wt, val, n - 1, W);
}
};
int main() {
vector<int> wt = {1, 2, 4, 5};
vector<int> val = {5, 4, 8, 6};
int W = 5;
int n = wt.size();
//Create an instance of Solution class
Solution sol;
// Call the function to find the minimum coins
int result = sol.knapsack01(wt, val, n, W);
// Output the result
cout << "The Maximum value of items is " << result << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
import java.util.*;
class Solution {
// Function to solve 0/1 Knapsack problem using memoization
private int func(int[] wt, int[] val, int ind, int W) {
/* Base case: If there are no items left
or the knapsack has no capacity, return 0 */
if (ind == 0 || W == 0) {
return 0;
}
/* Calculate the maximum value by either
excluding the current item or including it */
int notTaken = func(wt, val, ind - 1, W);
int taken = 0;
/* Check if the current item can be included
without exceeding the knapsack's capacity */
if (wt[ind] <= W) {
taken = val[ind] + func(wt, val, ind - 1, W - wt[ind]);
}
// Return the result
return Math.max(notTaken, taken);
}
// Function to solve the 0/1 Knapsack problem
public int knapsack01(int[] wt, int[] val, int n, int W) {
return func(wt, val, n - 1, W);
}
public static void main(String[] args) {
int[] wt = {1, 2, 4, 5};
int[] val = {5, 4, 8, 6};
int W = 5;
int n = wt.length;
// Create an instance of Solution class
Solution sol = new Solution();
// Call the function to find the maximum value
int result = sol.knapsack01(wt, val, n, W);
// Output the result
System.out.println("The Maximum value of items is " + result);
}
}
123456789101112131415161718192021222324252627282930313233343536373839
class Solution:
# Function to solve 0/1 Knapsack problem using memoization
def func(self, wt, val, ind, W):
""" Base case: If there are no items left
or the knapsack has no capacity, return 0 """
if ind == 0 or W == 0:
return 0
""" Calculate the maximum value by either
excluding the current item or including it """
notTaken = self.func(wt, val, ind - 1, W)
taken = 0
""" Check if the current item can be included
without exceeding the knapsack's capacity"""
if wt[ind] <= W:
taken = val[ind] + self.func(wt, val, ind - 1, W - wt[ind])
# Return the result
return max(notTaken, taken)
# Function to solve the 0/1 Knapsack problem
def knapsack01(self, wt, val, n, W):
return self.func(wt, val, n - 1, W)
wt = [1, 2, 4, 5]
val = [5, 4, 8, 6]
W = 5
n = len(wt)
# Create an instance of Solution class
sol = Solution()
# Call the function to find the maximum value
result = sol.knapsack01(wt, val, n, W)
# Output the result
print("The Maximum value of items is", result)
1234567891011121314151617181920212223242526272829303132333435363738394041424344
class Solution {
// Function to solve 0/1 Knapsack problem using memoization
func(wt, val, ind, W) {
/* Base case: If there are no items left
or the knapsack has no capacity, return 0 */
if (ind === 0 || W === 0) {
return 0;
}
/* Calculate the maximum value by either
excluding the current item or including it */
let notTaken = this.func(wt, val, ind - 1, W);
let taken = 0;
/* Check if the current item can be included
without exceeding the knapsack's capacity */
if (wt[ind] <= W) {
taken = val[ind] + this.func(wt, val, ind - 1, W - wt[ind]);
}
// Store the result in the DP table and return
return Math.max(notTaken, taken);
}
// Function to solve the 0/1 Knapsack problem
knapsack01(wt, val, n, W) {
return this.func(wt, val, n - 1, W);
}
}
const wt = [1, 2, 4, 5];
const val = [5, 4, 8, 6];
const W = 5;
const n = wt.length;
// Create an instance of Solution class
const sol = new Solution();
// Call the function to find the maximum value
const result = sol.knapsack01(wt, val, n, W);
// Output the result
console.log("The Maximum value of items is " + result);
Complexity Analysis:
Time Complexity: O(2N), Where N is size of the array. As there are 2 choices for each index.Space Complexity:O(N), As we are using a recursion stack space of N.
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
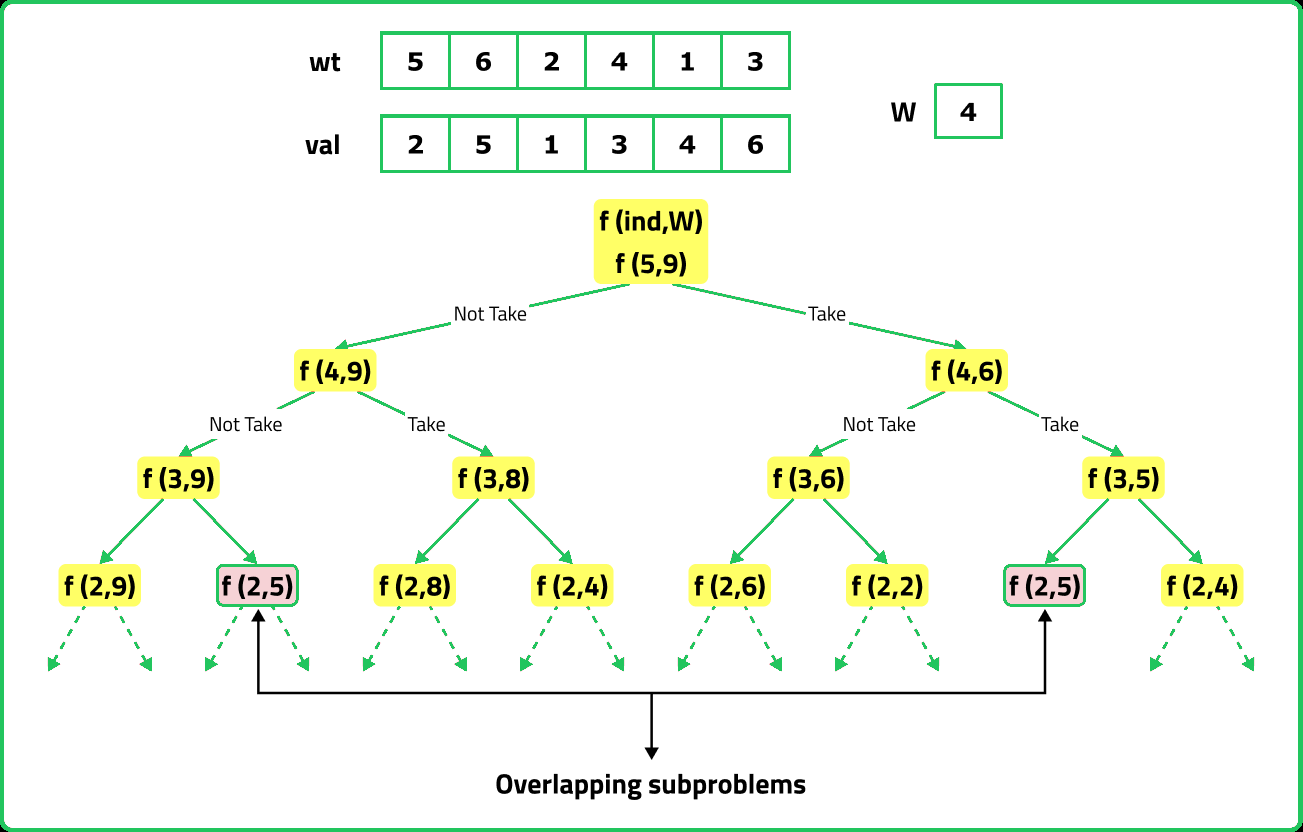
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][W+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The size of the input array is ‘N’, so the index will always lie between ‘0’ and ‘n-1’. The capacity can take any value between ‘0’ and ‘W’. Therefore 2D dp array(dp[n][W+1]) is needed.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
// Function to solve the 0/1 Knapsack problem with arrays
int func(vector<int> &wt, vector<int> &val, int ind, int W, vector<vector<int>>& dp) {
/* Base case: If there are no items left
or the knapsack has no capacity, return 0 */
if (ind < 0 || W == 0) {
return 0;
}
/* If the result for this state is
already calculated, return it */
if (dp[ind][W] != -1) {
return dp[ind][W];
}
/* Calculate the maximum value by either
excluding the current item or including it */
int notTaken = func(wt, val, ind - 1, W, dp);
int taken = 0;
/* Check if the current item can be included
without exceeding the knapsack's capacity */
if (wt[ind] <= W) {
taken = val[ind] + func(wt, val, ind - 1, W - wt[ind], dp);
}
// Store the result in the DP table and return
return dp[ind][W] = max(notTaken, taken);
}
public:
/* Function to return max value that
can be put in knapsack of capacity W.*/
int knapsack01(vector<int> wt, vector<int> val, int n, int W) {
// Initialize DP table with -1
vector<vector<int>> dp(n, vector<int>(W + 1, -1));
return func(wt, val, n - 1, W, dp);
}
};
int main() {
vector<int> wt = {1, 2, 4, 5};
vector<int> val = {5, 4, 8, 6};
int W = 5;
int n = wt.size();
//Create an instance of Solution class
Solution sol;
cout << "The Maximum value of items is " << sol.knapsack01(wt, val, n, W);
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
import java.util.*;
class Solution {
// Function to solve the 0/1 Knapsack problem with arrays
private int func(int[] wt, int[] val, int ind, int W, int[][] dp) {
/* Base case: If there are no items left
or the knapsack has no capacity, return 0 */
if (ind < 0 || W == 0) {
return 0;
}
/* If the result for this state is
already calculated, return it */
if (dp[ind][W] != -1) {
return dp[ind][W];
}
/* Calculate the maximum value by either
excluding the current item or including it */
int notTaken = func(wt, val, ind - 1, W, dp);
int taken = 0;
/* Check if the current item can be included
without exceeding the knapsack's capacity */
if (wt[ind] <= W) {
taken = val[ind] + func(wt, val, ind - 1, W - wt[ind], dp);
}
// Store the result in the DP table and return
dp[ind][W] = Math.max(notTaken, taken);
return dp[ind][W];
}
public int knapsack01(int[] wt, int[] val, int n, int W) {
// Initialize DP table with -1
int[][] dp = new int[n][W + 1];
for (int[] row : dp) {
Arrays.fill(row, -1);
}
return func(wt, val, n - 1, W, dp);
}
public static void main(String[] args) {
int[] wt = {1, 2, 4, 5};
int[] val = {5, 4, 8, 6};
int W = 5;
int n = wt.length;
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("The Maximum value of items is " + sol.knapsack01(wt, val, n, W));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344
class Solution:
# Function to solve the 0/1 Knapsack problem with arrays
def func(self, wt, val, ind, W, dp):
""" Base case: If there are no items left
or the knapsack has no capacity, return 0"""
if ind < 0 or W == 0:
return 0
""" If the result for this state is
already calculated, return it"""
if dp[ind][W] != -1:
return dp[ind][W]
""" Calculate the maximum value by either
excluding the current item or including it"""
not_taken = self.func(wt, val, ind - 1, W, dp)
taken = 0
""" Check if the current item can be included
without exceeding the knapsack's capacity"""
if wt[ind] <= W:
taken = val[ind] + self.func(wt, val, ind - 1, W - wt[ind], dp)
# Store the result in the DP table and return
dp[ind][W] = max(not_taken, taken)
return dp[ind][W]
def knapsack01(self, wt, val, n, W):
# Initialize DP table with -1
dp = [[-1 for _ in range(W + 1)] for _ in range(n)]
return self.func(wt, val, n - 1, W, dp)
# Main execution
if __name__ == "__main__":
wt = [1, 2, 4, 5]
val = [5, 4, 8, 6]
W = 5
n = len(wt)
# Create an instance of Solution class
sol = Solution()
print("The Maximum value of items is", sol.knapsack01(wt, val, n, W))
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849
class Solution {
// Function to solve the 0/1 Knapsack problem with arrays
func(wt, val, ind, W, dp) {
/* Base case: If there are no items left
or the knapsack has no capacity, return 0*/
if (ind < 0 || W === 0) {
return 0;
}
/* If the result for this state is
already calculated, return it*/
if (dp[ind][W] !== -1) {
return dp[ind][W];
}
/* Calculate the maximum value by either
excluding the current item or including it*/
const notTaken = this.func(wt, val, ind - 1, W, dp);
let taken = 0;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= W) {
taken = val[ind] + this.func(wt, val, ind - 1, W - wt[ind], dp);
}
// Store the result in the DP table and return
dp[ind][W] = Math.max(notTaken, taken);
return dp[ind][W];
}
knapsack01(wt, val, n, W) {
// Initialize DP table with -1
const dp = Array.from({ length: n }, () => Array(W + 1).fill(-1));
return this.func(wt, val, n - 1, W, dp);
}
}
// Main execution
const wt = [1, 2, 4, 5];
const val = [5, 4, 8, 6];
const W = 5;
const n = wt.length;
// Create an instance of Solution class
const sol = new Solution();
console.log("The Maximum value of items is", sol.knapsack01(wt, val, n, W));
Complexity Analysis:
Time Complexity: O(N*W), where N is the size of the array and W is the capacity of the knapsack. There are N*W states therefore at max ‘N*W’ new problems will be solved.Space Complexity:O(N*W) + O(N), We are using a recursion stack space(O(N)) and a 2D array ( O(N*W)).
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n][W+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The size of the input array is ‘N’, so the index will always lie between ‘0’ and ‘n-1’. The capacity can take any value between ‘0’ and ‘W’. Therefore 2D dp array(dp[n][W+1]) is needed. Set its type as int and initialize it as 0.
- Setting Base Cases in the Array: In the recursive code, our base condition was when ind == 0, it meant we were at the first item, so in that case were checking whether this item’s weight is less than or equal to the current capacity W, if it was, we were simply returning its value (val[0]) else we were returning 0. So, will set the same value for 'ind' = 0 in the dp array.
- Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array. First loop will run from 1 to n-1 as we are done for the ind = 0 for the base case and the second loop will run from 0 to 'W'.
- Now, following the same logic as discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.
- Returning the answer: At last dp[n-1][W] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
// Function to solve the 0/1 Knapsack problem
int knapsack01(vector<int>& wt, vector<int>& val, int n, int W) {
/* Declare a 2D DP table with dimensions
n x W+1 and initialize it with zeros*/
vector<vector<int>> dp(n, vector<int>(W + 1, 0));
/* Base condition: Fill in the first
row for the weight of the first item*/
for (int i = wt[0]; i <= W; i++) {
dp[0][i] = val[0];
}
// Fill in DP table using a bottom-up approach
for (int ind = 1; ind < n; ind++) {
for (int cap = 0; cap <= W; cap++) {
/* Calculate the maximum value by either
excluding the current item or including it*/
int notTaken = dp[ind - 1][cap];
int taken = INT_MIN;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= cap) {
taken = val[ind] + dp[ind - 1][cap - wt[ind]];
}
// Update the DP table
dp[ind][cap] = max(notTaken, taken);
}
}
// The final result is in last cell
return dp[n - 1][W];
}
};
int main() {
vector<int> wt = {1, 2, 4, 5};
vector<int> val = {5, 4, 8, 6};
int W = 5;
int n = wt.size();
//Create an instance of Solution class
Solution sol;
// Call the function to find the minimum coins
int result = sol.knapsack01(wt, val, n, W);
// Output the result
cout << "The Maximum value of items is " << result << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
import java.util.Arrays;
class Solution {
// Function to solve the 0/1 Knapsack problem
public int knapsack01(int[] wt, int[] val, int n, int W) {
/* Declare a 2D DP table with dimensions
n x W+1 and initialize it with zeros*/
int[][] dp = new int[n][W + 1];
/* Base condition: Fill in the first
row for the weight of the first item*/
for (int i = wt[0]; i <= W; i++) {
dp[0][i] = val[0];
}
// Fill in DP table using a bottom-up approach
for (int ind = 1; ind < n; ind++) {
for (int cap = 0; cap <= W; cap++) {
/* Calculate the maximum value by either
excluding the current item or including it*/
int notTaken = dp[ind - 1][cap];
int taken = Integer.MIN_VALUE;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= cap) {
taken = val[ind] + dp[ind - 1][cap - wt[ind]];
}
// Update the DP table
dp[ind][cap] = Math.max(notTaken, taken);
}
}
// The final result is in the last cell
return dp[n - 1][W];
}
public static void main(String[] args) {
int[] wt = {1, 2, 4, 5};
int[] val = {5, 4, 8, 6};
int W = 5;
int n = wt.length;
// Create an instance of Solution class
Solution sol = new Solution();
// Call the function to find the maximum value
int result = sol.knapsack01(wt, val, n, W);
// Output the result
System.out.println("The Maximum value of items is " + result);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445
class Solution:
# Function to solve 0/1 Knapsack problem
def knapsack01(self, wt, val, n, W):
""" Declare a 2D DP table with dimensions
n x W+1 and initialize it with zeros"""
dp = [[0] * (W + 1) for _ in range(n)]
""" Base condition: Fill in the first row
for the weight of the first item"""
for i in range(wt[0], W + 1):
dp[0][i] = val[0]
# Fill in DP table using a bottom-up approach
for ind in range(1, n):
for cap in range(W + 1):
""" Calculate the maximum value by either
excluding the current item or including it"""
notTaken = dp[ind - 1][cap]
taken = float('-inf')
""" Check if the current item can be included
without exceeding the knapsack's capacity"""
if wt[ind] <= cap:
taken = val[ind] + dp[ind - 1][cap - wt[ind]]
# Update the DP table
dp[ind][cap] = max(notTaken, taken)
# The final result is in the last cell
return dp[n - 1][W]
wt = [1, 2, 4, 5]
val = [5, 4, 8, 6]
W = 5
n = len(wt)
# Create an instance of Solution class
sol = Solution()
# Call the function to find the maximum value
result = sol.knapsack01(wt, val, n, W)
# Output the result
print("The Maximum value of items is", result)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051
class Solution {
// Function to solve the 0/1 Knapsack problem
knapsack01(wt, val, n, W) {
/* Declare a 2D DP table with dimensions
n x W+1 and initialize it with zeros*/
let dp = Array.from({ length: n }, () => Array(W + 1).fill(0));
/* Base condition: Fill in the first
row for the weight of the first item*/
for (let i = wt[0]; i <= W; i++) {
dp[0][i] = val[0];
}
// Fill in DP table using a bottom-up approach
for (let ind = 1; ind < n; ind++) {
for (let cap = 0; cap <= W; cap++) {
/* Calculate the maximum value by either
excluding the current item or including it*/
let notTaken = dp[ind - 1][cap];
let taken = Number.NEGATIVE_INFINITY;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= cap) {
taken = val[ind] + dp[ind - 1][cap - wt[ind]];
}
// Update the DP table
dp[ind][cap] = Math.max(notTaken, taken);
}
}
// The final result is in the last cell
return dp[n - 1][W];
}
}
const wt = [1, 2, 4, 5];
const val = [5, 4, 8, 6];
const W = 5;
const n = wt.length;
// Create an instance of Solution class
const sol = new Solution();
// Call the function to find the maximum value
const result = sol.knapsack01(wt, val, n, W);
// Output the result
console.log("The Maximum value of items is " + result);
Complexity Analysis:
Time Complexity: O(N*W), where N is the size of the array. As two nested loops are used for the calculations.Space Complexity:O(N*W), As a 2D array of size N*W is used.
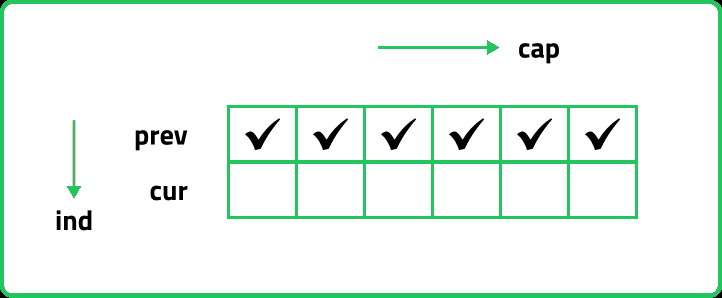
If we observe the relation, dp[ind][cap] = max(dp[ind-1][cap] ,dp[ind-1][cap-wt[ind]]. We find that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it. We will be space optimizing this solution using only one row.
Intuition:
If we closely observe, we fill in the following manner in two-row space optimization:
- We will initialize the first row and then using its values we will the next row.
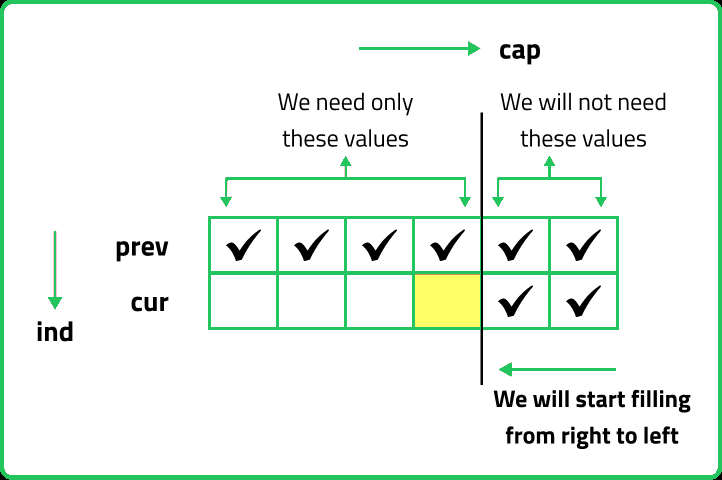
- If we clearly see the values required: dp[ind-1][cap] and dp[ind-1][cap - wt[ind]], we can say that if we are at a column cap, we will only require the values shown in the green region and none in the red region shown in the below image ( because cap - wt[ind] will always be less than the cap).
- As we don’t want values from the right, we can start filling this new row from the right rather than the left.
- Now here is the catch, if we are filling from the right and at any time we need the previous row’s value of the leftward columns only, why do we need to have two rows in the first place? We can use a single row and overwrite the new computed values on itself in order to store it.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
// Function to solve the 0/1 Knapsack problem
int knapsack01(vector<int>& wt, vector<int>& val, int n, int W) {
/* Initialize a vector 'prev' to represent
the previous row of the DP table*/
vector<int> prev(W + 1, 0);
/* Base condition: Fill in 'prev'
for the weight of the first item*/
for (int i = wt[0]; i <= W; i++) {
prev[i] = val[0];
}
// Fill in the table using a bottom-up approach
for (int ind = 1; ind < n; ind++) {
for (int cap = W; cap >= 0; cap--) {
/* Calculate the maximum value by either
excluding the current item or including it*/
int notTaken = prev[cap];
int taken = INT_MIN;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= cap) {
taken = val[ind] + prev[cap - wt[ind]];
}
// Update 'prev' for the current capacity
prev[cap] = max(notTaken, taken);
}
}
/* The final result is in the
last cell of the 'prev' vector*/
return prev[W];
}
};
int main() {
vector<int> wt = {1, 2, 4, 5};
vector<int> val = {5, 4, 8, 6};
int W = 5;
int n = wt.size();
//Create an instance of Solution class
Solution sol;
// Call the function to find the minimum coins
int result = sol.knapsack01(wt, val, n, W);
// Output the result
cout << "The Maximum value of items is " << result << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
import java.util.*;
class Solution {
// Function to solve the 0/1 Knapsack problem
public int knapsack01(int[] wt, int[] val, int n, int W) {
/* Initialize a vector 'prev' to represent
the previous row of the DP table*/
int[] prev = new int[W + 1];
/* Base condition: Fill in 'prev'
for the weight of the first item*/
for (int i = wt[0]; i <= W; i++) {
prev[i] = val[0];
}
// Fill in the table using a bottom-up approach
for (int ind = 1; ind < n; ind++) {
for (int cap = W; cap >= 0; cap--) {
/* Calculate the maximum value by either
excluding the current item or including it*/
int notTaken = prev[cap];
int taken = Integer.MIN_VALUE;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= cap) {
taken = val[ind] + prev[cap - wt[ind]];
}
// Update 'prev' for the current capacity
prev[cap] = Math.max(notTaken, taken);
}
}
/* The final result is in the
last cell of the 'prev' vector*/
return prev[W];
}
public static void main(String[] args) {
int[] wt = {1, 2, 4, 5};
int[] val = {5, 4, 8, 6};
int W = 5;
int n = wt.length;
// Create an instance of Solution class
Solution sol = new Solution();
// Call the function to find the maximum value
int result = sol.knapsack01(wt, val, n, W);
// Output the result
System.out.println("The Maximum value of items is " + result);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
class Solution:
# Function to solve the 0/1 Knapsack problem
def knapsack01(self, wt, val, n, W):
""" Initialize a vector 'prev' to represent
the previous row of the DP table"""
prev = [0] * (W + 1)
""" Base condition: Fill in 'prev'
for the weight of the first item"""
for i in range(wt[0], W + 1):
prev[i] = val[0]
# Fill in the table using a bottom-up approach
for ind in range(1, n):
for cap in range(W, -1, -1):
""" Calculate the maximum value by either
excluding the current item or including it"""
notTaken = prev[cap]
taken = float('-inf')
""" Check if the current item can be included
without exceeding the knapsack's capacity"""
if wt[ind] <= cap:
taken = val[ind] + prev[cap - wt[ind]]
# Update 'prev' for the current capacity
prev[cap] = max(notTaken, taken)
""" The final result is in the
last cell of the 'prev' vector"""
return prev[W]
wt = [1, 2, 4, 5]
val = [5, 4, 8, 6]
W = 5
n = len(wt)
# Create an instance of Solution class
sol = Solution()
# Call the function to find the maximum value
result = sol.knapsack01(wt, val, n, W)
# Output the result
print("The Maximum value of items is", result)
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
class Solution {
// Function to solve the 0/1 Knapsack problem
knapsack01(wt, val, n, W) {
/* Initialize a vector 'prev' to represent
the previous row of the DP table*/
let prev = Array(W + 1).fill(0);
/* Base condition: Fill in 'prev'
for the weight of the first item*/
for (let i = wt[0]; i <= W; i++) {
prev[i] = val[0];
}
// Fill in the table using a bottom-up approach
for (let ind = 1; ind < n; ind++) {
for (let cap = W; cap >= 0; cap--) {
/* Calculate the maximum value by either
excluding the current item or including it*/
let notTaken = prev[cap];
let taken = Number.NEGATIVE_INFINITY;
/* Check if the current item can be included
without exceeding the knapsack's capacity*/
if (wt[ind] <= cap) {
taken = val[ind] + prev[cap - wt[ind]];
}
// Update 'prev' for the current capacity
prev[cap] = Math.max(notTaken, taken);
}
}
/* The final result is in the
last cell of the 'prev' vector*/
return prev[W];
}
}
const wt = [1, 2, 4, 5];
const val = [5, 4, 8, 6];
const W = 5;
const n = wt.length;
// Create an instance of Solution class
const sol = new Solution();
// Call the function to find the maximum value
const result = sol.knapsack01(wt, val, n, W);
// Output the result
console.log("The Maximum value of items is " + result);
Complexity Analysis:
Time Complexity: O(N*W), where N is the size of the array. As two nested loops are used for the calculations.Space Complexity:O(W), We are using an external array of size ‘W+1’ to store only one row.
Frequently Occurring Doubts
Q: What if an item’s weight is 0 but has a positive value?
A: In standard knapsack problems, we assume weights are positive. If weight is 0, an item can be selected infinitely, making it an unbounded knapsack.
Q: Can we use a greedy approach instead of DP?
A: No, because a greedy approach fails when item values don’t align proportionally with their weights.
Interview Followup Questions
Q: What if we had a limit on the number of times each item can be picked (Bounded Knapsack)?
A: Use a 3D DP table (dp[i][w][c]), where c tracks the count of times an item is used.
Q: How can this problem be solved using recursion with memoization?
A: Define knapsack(i,w)=max(knapsack(i−1,w),knapsack(i−1,w−wt[i])+val[i]). Use top-down memoization (O(N × W) complexity).
Notes
Code
✅ Testcase
Input: {'W': '50', 'wt': '[10, 20, 30]', 'val': '[60, 100, 120]'}
Expected:
220
220
Actual: -
Time: -
sec
Status: Waiting
Input: {'W': '10', 'wt': '[5, 4, 6, 3]', 'val': '[10, 40, 30, 50]'}
Expected:
90
90
Actual: -
Time: -
sec
Status: Waiting
Input: {'W': '10', 'wt': '[1, 2, 3, 8, 7, 4]', 'val': '[20, 5, 10, 40, 15, 25]'}
Expected:
60
60
Actual: -
Time: -
sec
Status: Waiting
Facts
- • Fun Fact: The concept behind this knapsack problem is practically used in Resource Allocation and Load Balancing in Cloud Computing
- • In cloud computing, resources (like processing power, storage, etc
- • ) are finite and there's a need to optimize
- • The knapsack problem revolves around optimizing the value of items that can fit in a limited-size knapsack, making it a perfect model for allocating finite resources
- • Choices must be made about which virtual machines or jobs to allocate to each server, so that server capacity (weight limit in knapsack) isn't exceeded and efficiency or performance (value in knapsack) is maximized
- • It's a key aspect in determining how to distribute loads in order to get the maximal utility