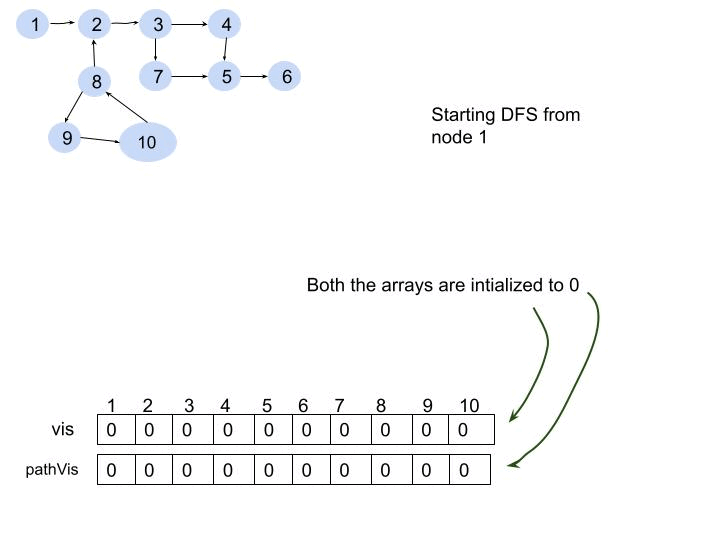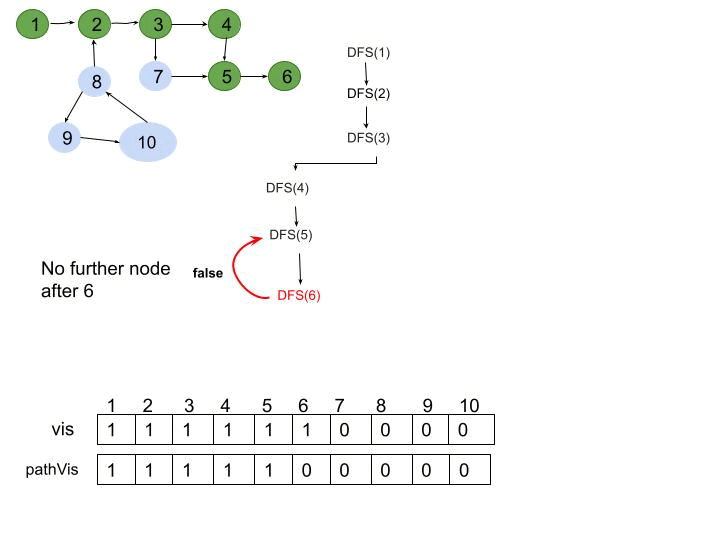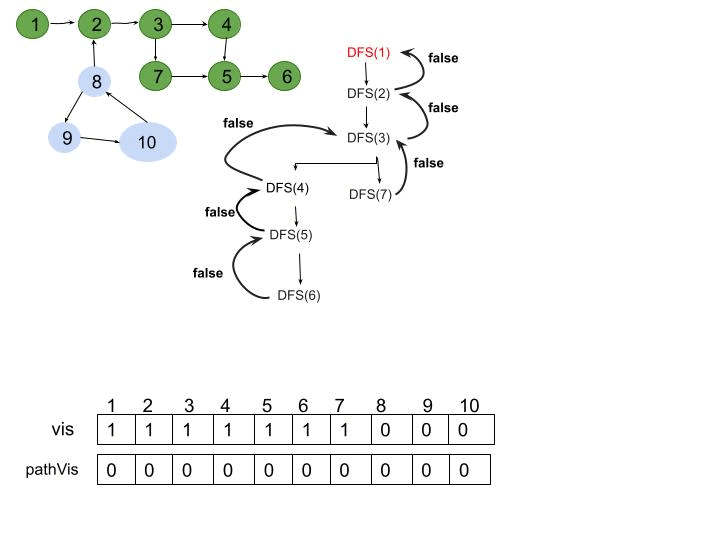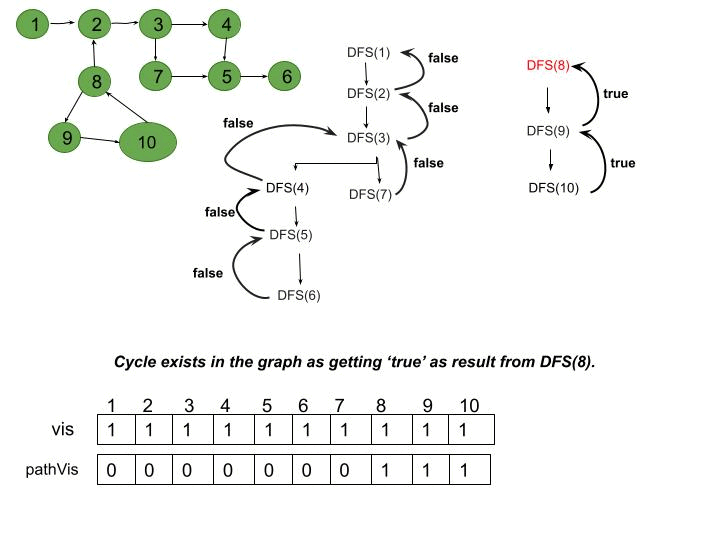
Detect a cycle in a directed graph
Graphs
Cycles
Hard
- Fun Fact: The problem of detecting cycles in a directed graph is essentially used in software dependency management systems
- These systems, such as NPM for JavaScript or Maven for Java, have to resolve various package dependencies while avoiding cycles
- A cycle would mean you have a circular dependency, which often leads to infinite recursion or other logical errors
- Thus, algorithms solving such problems are integral to the smooth operation of modern software development and operations
Given a directed graph with V vertices labeled from 0 to V-1. The graph is represented using an adjacency list where adj[i] lists all nodes connected to node. Determine if the graph contains any cycles.
Examples:
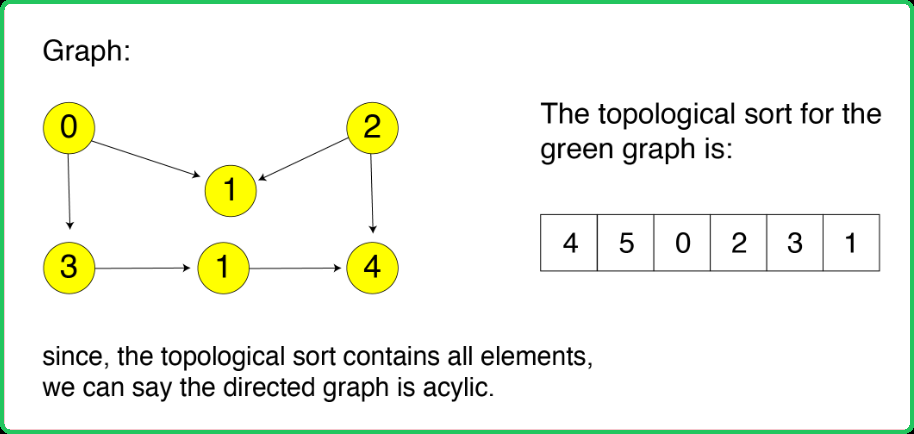
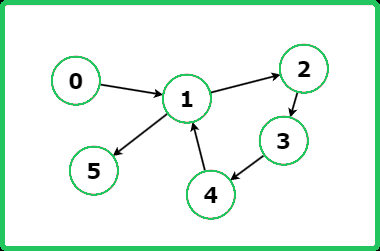
Input: V = 6, adj= [ [1], [2, 5], [3], [4], [1], [ ] ]
Output: True
Explanation: The graph contains a cycle: 1 -> 2 -> 3 -> 4 -> 1.
Input: V = 4, adj= [[1,2], [2], [], [0,2]]
Output: False
Explanation: The graph does not contain a cycle.
Input: V = 3, adj= [[1], [2], [0]]
Constraints
- E=number of edges
- 1 ≤ V, E ≤ 104
Hints
- "Use DFS with a recursion stack to track visited nodes. A cycle exists if a node is visited again while still being processed (present in the recursion stack)."
- "A DAG (Directed Acyclic Graph) can always be topologically sorted. If a valid topological sort is not possible (i.e., not all nodes are processed), a cycle exists."
Company Tags
Target
Broadcom
Morgan Stanley
Chewy
Johnson & Johnson
Instacart
Siemens Healthineers
Byju's
Mastercard
Goldman Sachs
AMD
PayPal
ARM
Walmart
Deloitte
Boston Consulting Group
Pinterest
McKinsey & Company
Shopify
Medtronic
DoorDash
Robinhood
Uber
Texas Instruments
GE Healthcare
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe