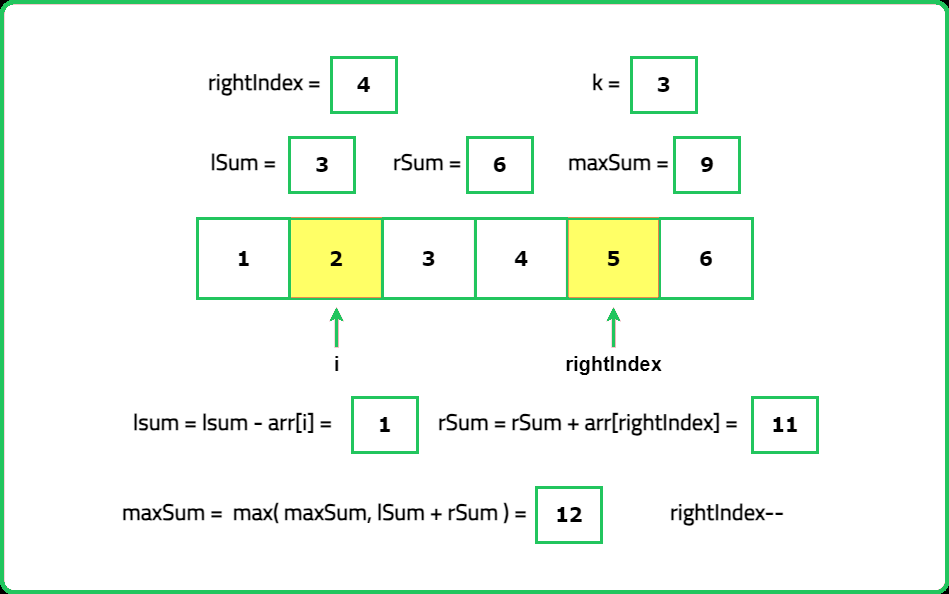
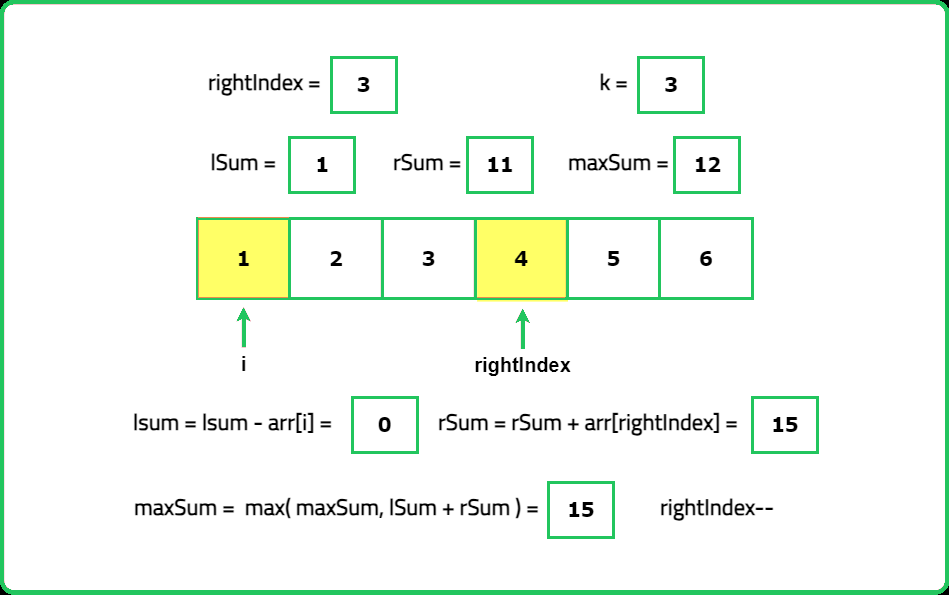
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to calculate the maximum
score after picking k cards*/
int maxScore(vector<int>& cardScore, int k) {
int lSum = 0, rSum = 0, maxSum = 0;
// Calculate the initial sum of the first k cards
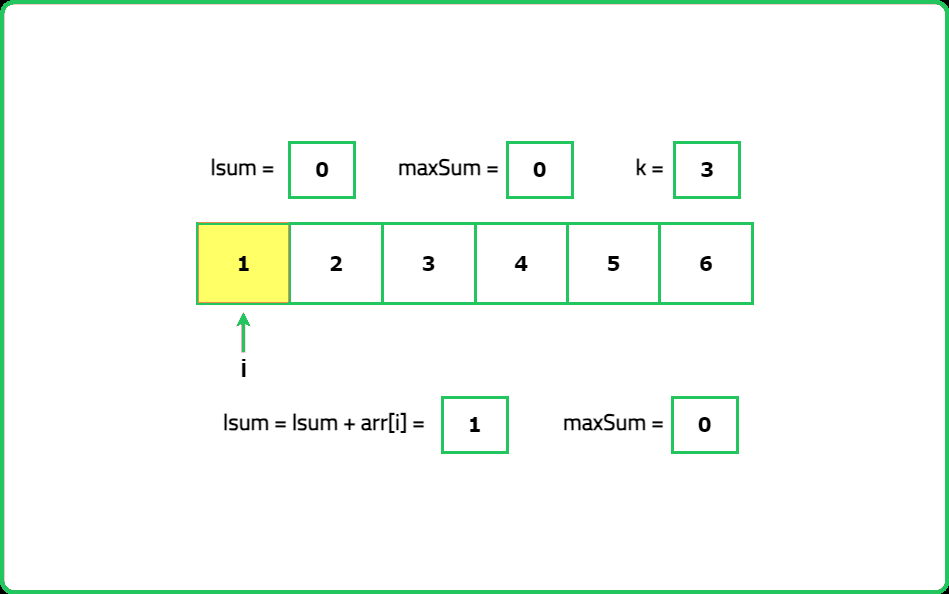
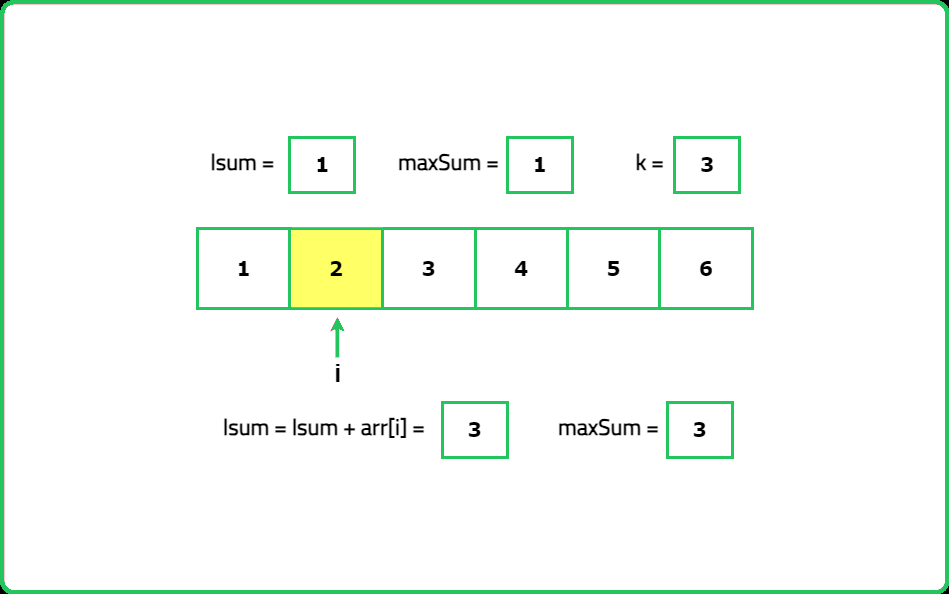
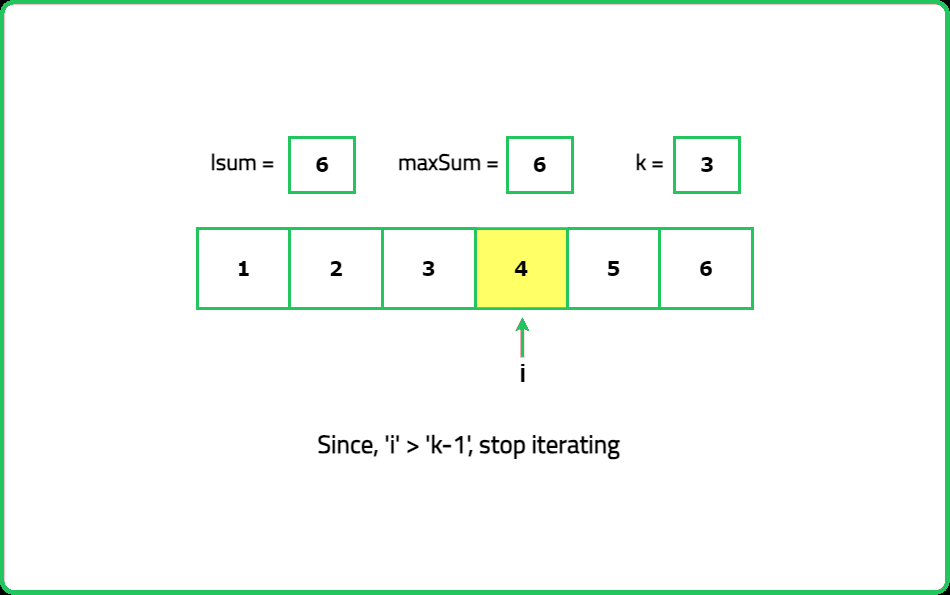
for (int i = 0; i < k; i++) {
lSum += cardScore[i];
/* Initialize maxSum with the
sum of the first k cards*/
maxSum = lSum;
}
//Initialize rightIndex to iterate array from last
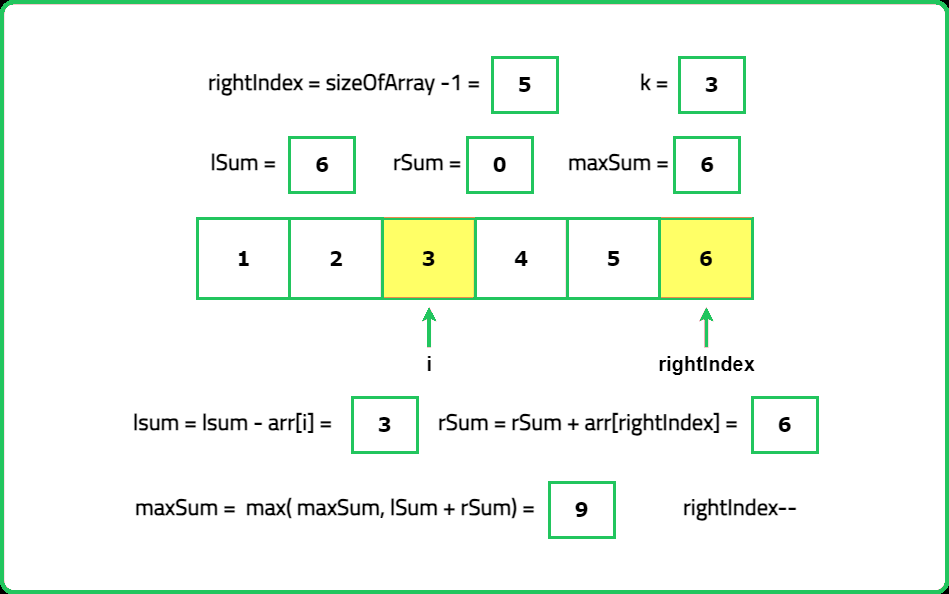
int rightIndex = cardScore.size() - 1;
for (int i = k - 1; i >= 0; i--) {
// Remove the score of the ith card from left sum
lSum -= cardScore[i];
/* Add the score of the card
from the right to the right sum*/
rSum += cardScore[rightIndex];
// Move to the next card from the right
rightIndex--;
// Update maxSum with the maximum sum found so far
maxSum = max(maxSum, lSum + rSum);
}
// Return the maximum score found
return maxSum;
}
};
int main() {
vector<int> nums = {1, 2, 3, 4, 5, 6};
// Create an instance of the Solution class
Solution sol;
int result = sol.maxScore(nums, 3);
// Output the maximum score
cout << "The maximum score is:\n";
cout << result << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354
import java.util.*;
class Solution {
/* Function to calculate the maximum
score after picking k cards */
public int maxScore(int[] cardScore, int k) {
int lSum = 0, rSum = 0, maxSum = 0;
// Calculate the initial sum of the first k cards
for (int i = 0; i < k; i++) {
lSum += cardScore[i];
/* Initialize maxSum with the
sum of the first k cards */
maxSum = lSum;
}
// Initialize rightIndex to iterate array from last
int rightIndex = cardScore.length - 1;
for (int i = k - 1; i >= 0; i--) {
// Remove the score of the ith card from left sum
lSum -= cardScore[i];
/* Add the score of the card
from the right to the right sum */
rSum += cardScore[rightIndex];
// Move to the next card from the right
rightIndex--;
// Update maxSum with the maximum sum found so far
maxSum = Math.max(maxSum, lSum + rSum);
}
// Return the maximum score found
return maxSum;
}
public static void main(String[] args) {
int[] nums = {1, 2, 3, 4, 5, 6};
// Create an instance of the Solution class
Solution sol = new Solution();
int result = sol.maxScore(nums, 3);
// Output the maximum score
System.out.println("The maximum score is:");
System.out.println(result);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
class Solution:
""" Function to calculate the maximum
score after picking k cards"""
def maxScore(self, cardScore, k):
lSum = 0
rSum = 0
maxSum = 0
# Calculate the initial sum of the first k cards
for i in range(k):
lSum += cardScore[i]
""" Initialize maxSum with the
sum of the first k cards"""
maxSum = lSum
# Initialize rightIndex to iterate array from last
rightIndex = len(cardScore) - 1
for i in range(k - 1, -1, -1):
# Remove the score of the ith card from left sum
lSum -= cardScore[i]
# Add the score of the card
# from the right to the right sum
rSum += cardScore[rightIndex]
# Move to the next card from the right
rightIndex -= 1
# Update maxSum with the maximum sum found so far
maxSum = max(maxSum, lSum + rSum)
# Return the maximum score found
return maxSum
nums = [1, 2, 3, 4, 5, 6]
# Create an instance of the Solution class
sol = Solution()
result = sol.maxScore(nums, 3)
# Output the maximum score
print("The maximum score is:")
print(result)
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
class Solution {
// Function to calculate the maximum
// score after picking k cards
maxScore(cardScore, k) {
let lSum = 0, rSum = 0, maxSum = 0;
// Calculate the initial sum of the first k cards
for (let i = 0; i < k; i++) {
lSum += cardScore[i];
/* Initialize maxSum with the
sum of the first k cards */
maxSum = lSum;
}
// Initialize rightIndex to iterate array from last
let rightIndex = cardScore.length - 1;
for (let i = k - 1; i >= 0; i--) {
// Remove the score of the ith card from left sum
lSum -= cardScore[i];
/* Add the score of the card
from the right to the right sum */
rSum += cardScore[rightIndex];
// Move to the next card from the right
rightIndex--;
// Update maxSum with the maximum sum found so far
maxSum = Math.max(maxSum, lSum + rSum);
}
// Return the maximum score found
return maxSum;
}
}
let nums = [1, 2, 3, 4, 5, 6];
// Create an instance of the Solution class
let sol = new Solution();
let result = sol.maxScore(nums, 3);
// Output the maximum score
console.log("The maximum score is:");
console.log(result);