Count number of Nice subarrays
Sliding Window / 2 Pointer
Counting Subarrays / Substrings Problems
Hard
- This kind of problem is commonly seen in data analysis or data science domains where there is a need to analyze subarrays or sub-data-frames for given conditions
- A real-world application might be the analysis of user behavior patterns in tech companies, such as Netflix or YouTube, where they need to identify consecutive streams (i
- e
- , subarrays) with some specific characteristics (in the problem, it's 'k odd numbers')
- The retrieved results from this analysis can help to personalize content for users, improving user engagement with the platform
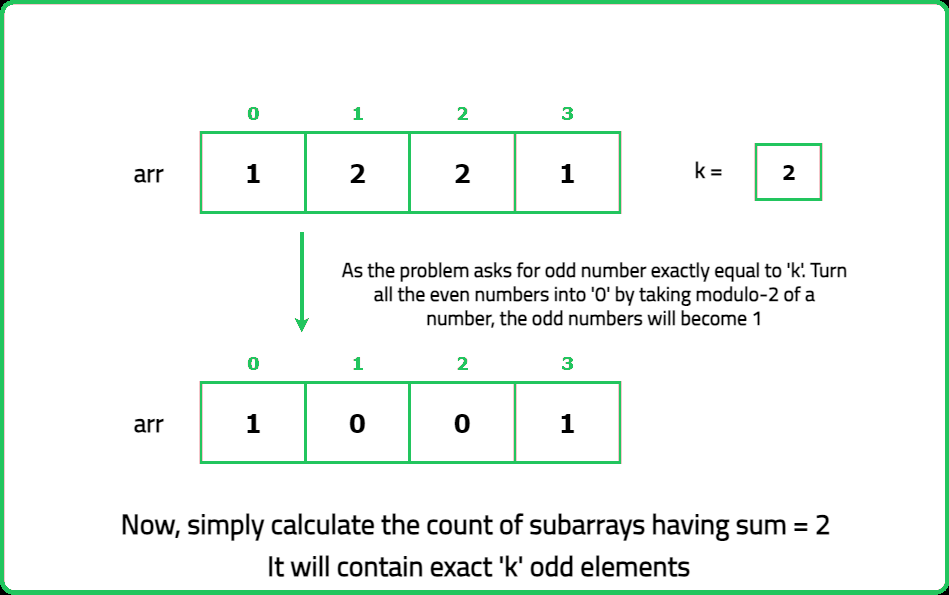
Given an array nums and an integer k. An array is called nice if and only if it contains k odd numbers. Find the number of nice subarrays in the given array nums.
A subarray is continuous part of the array.
Examples:
Input : nums = [1, 1, 2, 1, 1] , k = 3
Output : 2
Explanation : The subarrays with three odd numbers are
[1, 1, 2, 1]
[1, 2, 1, 1]
Input : nums = [4, 8, 2] , k = 1
Output : 0
Explanation : The array does not contain any odd number.
Input : nums = [41, 3, 5] , k = 2
Constraints
- 1 <= nums.length <= 5*104
- 1 <= nums[i] <= 105
- 1 <= k <= nums.length
Hints
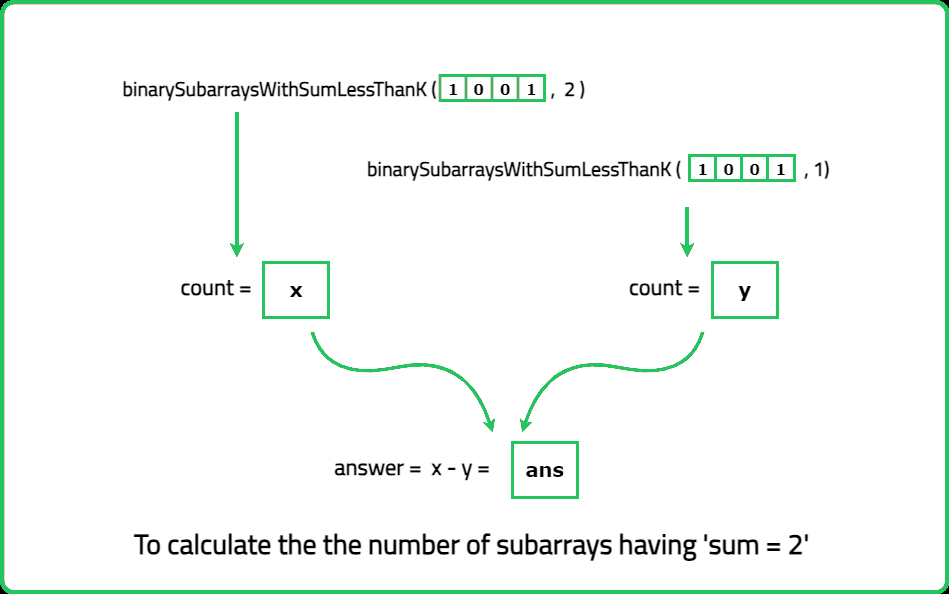
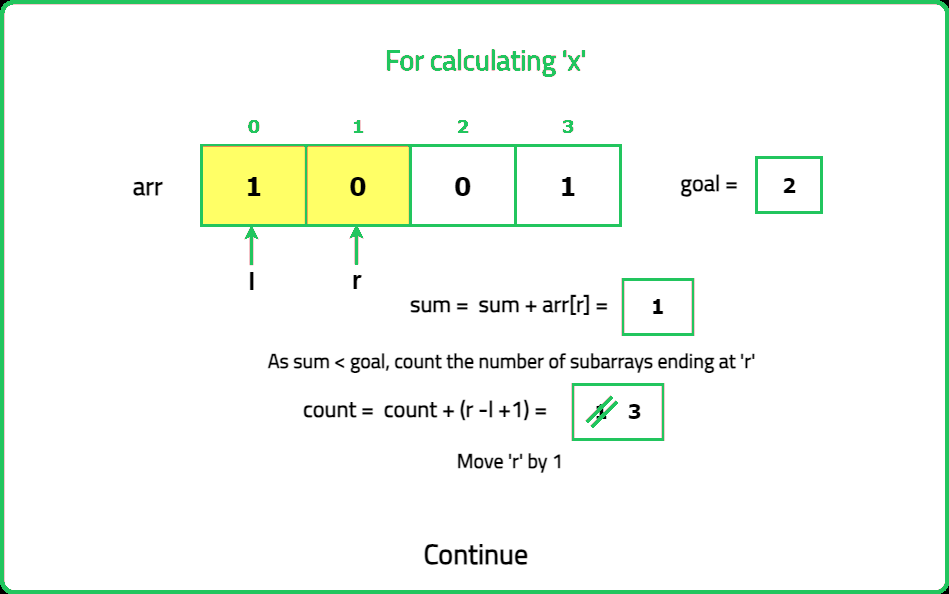
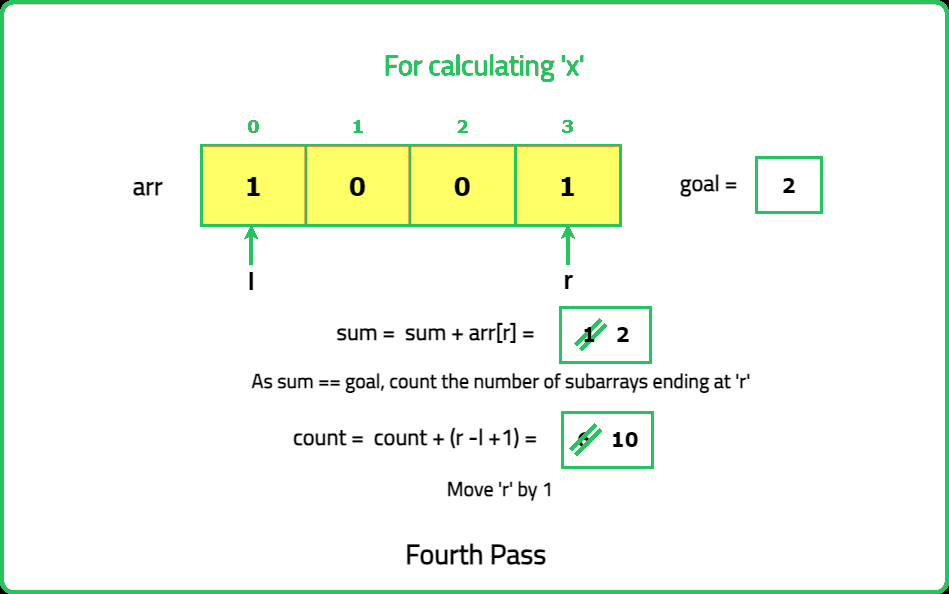
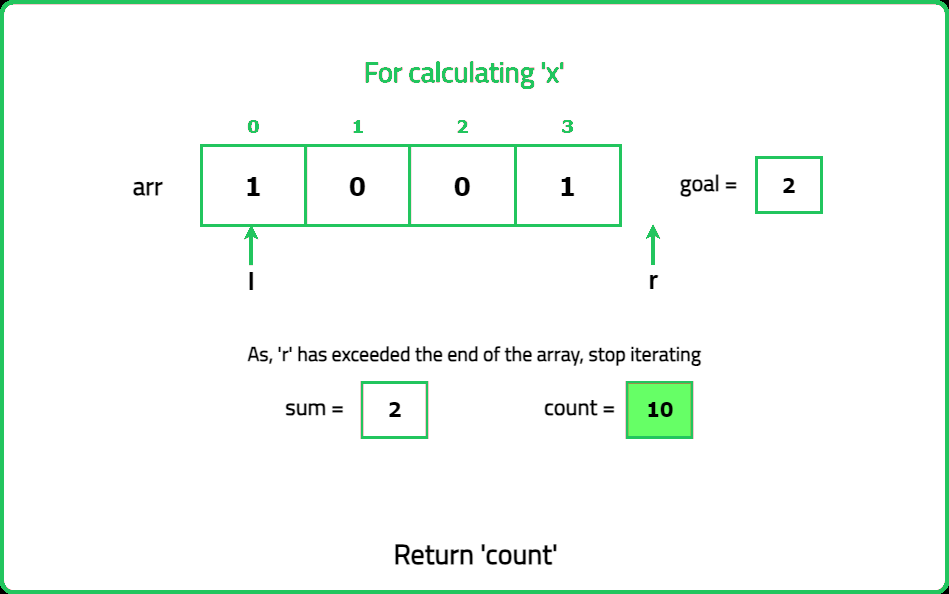
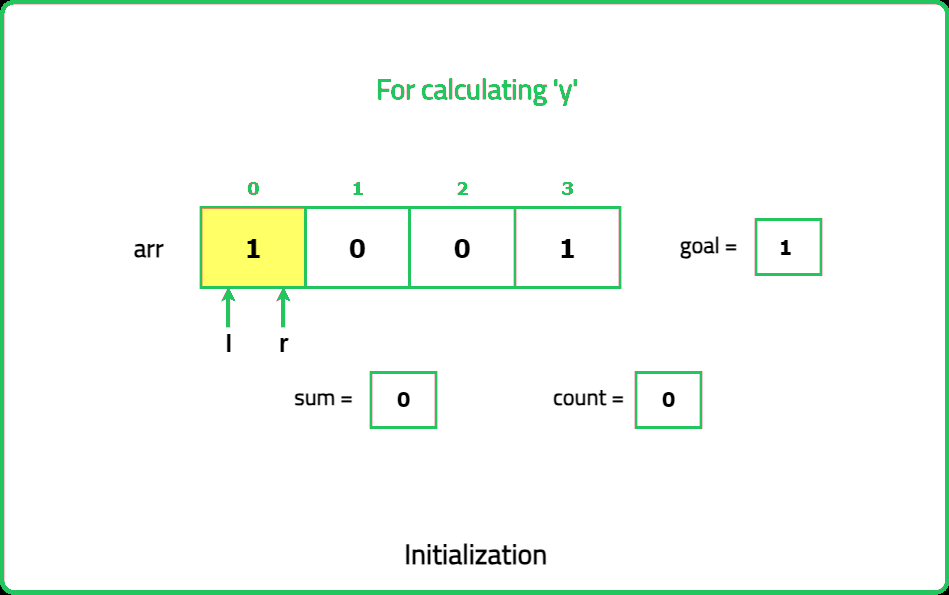
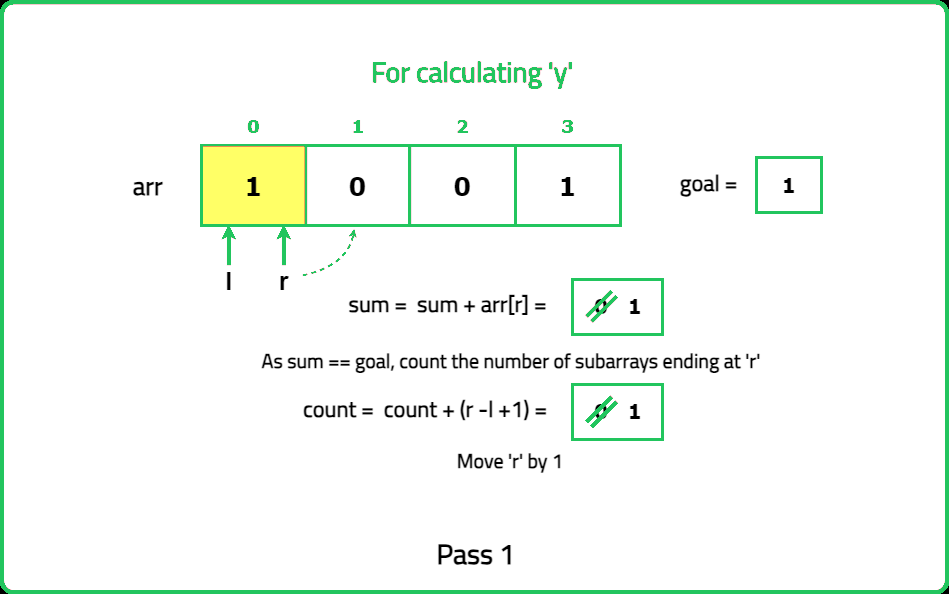
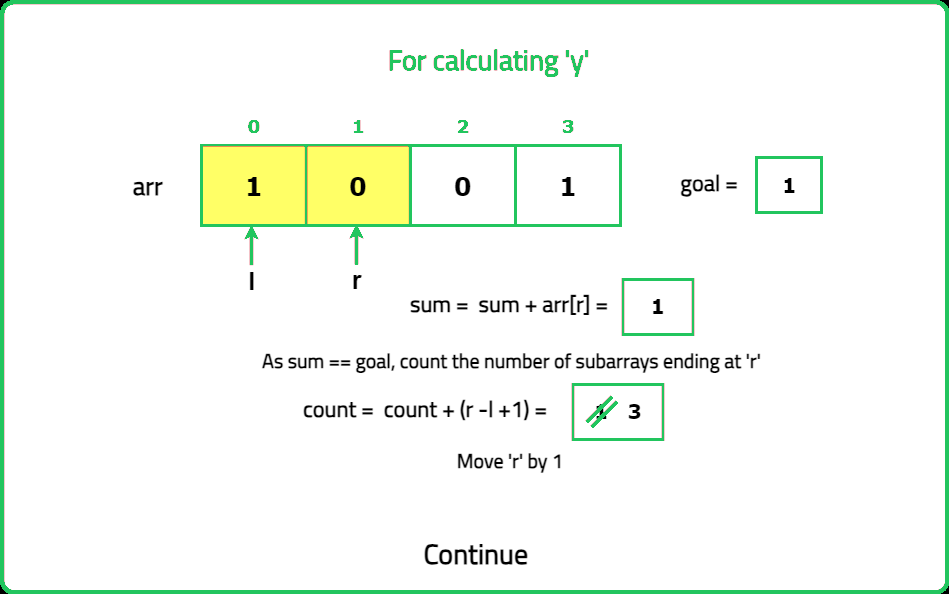
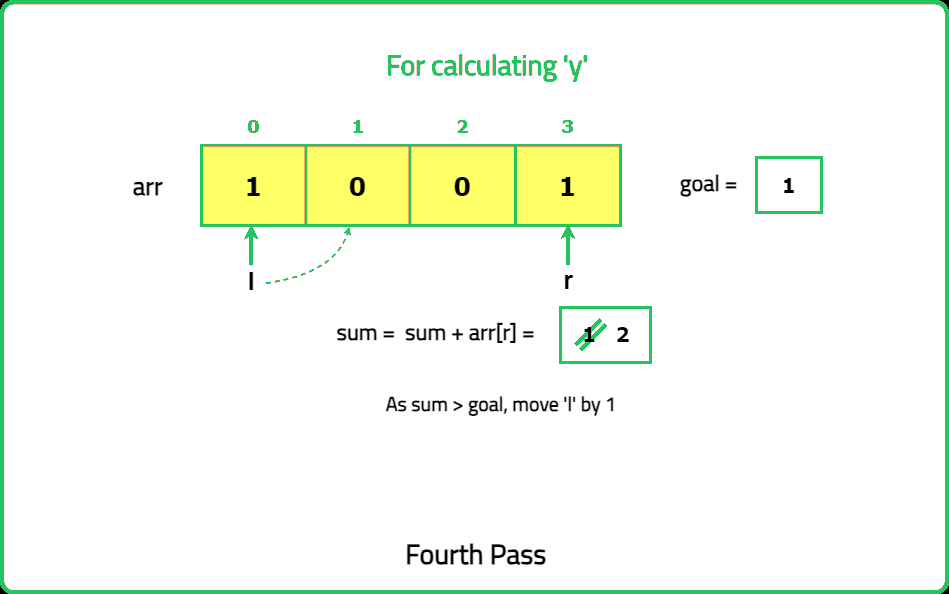
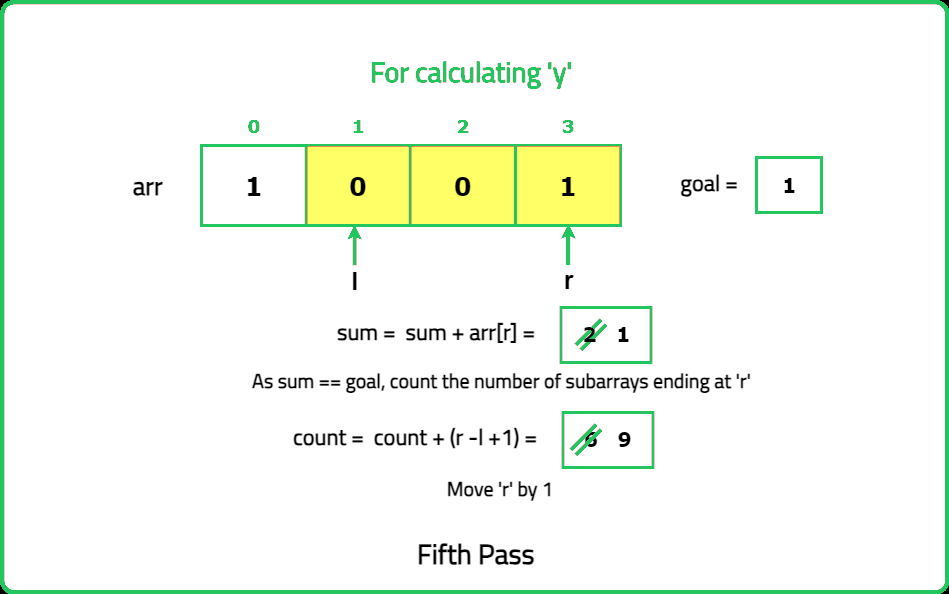
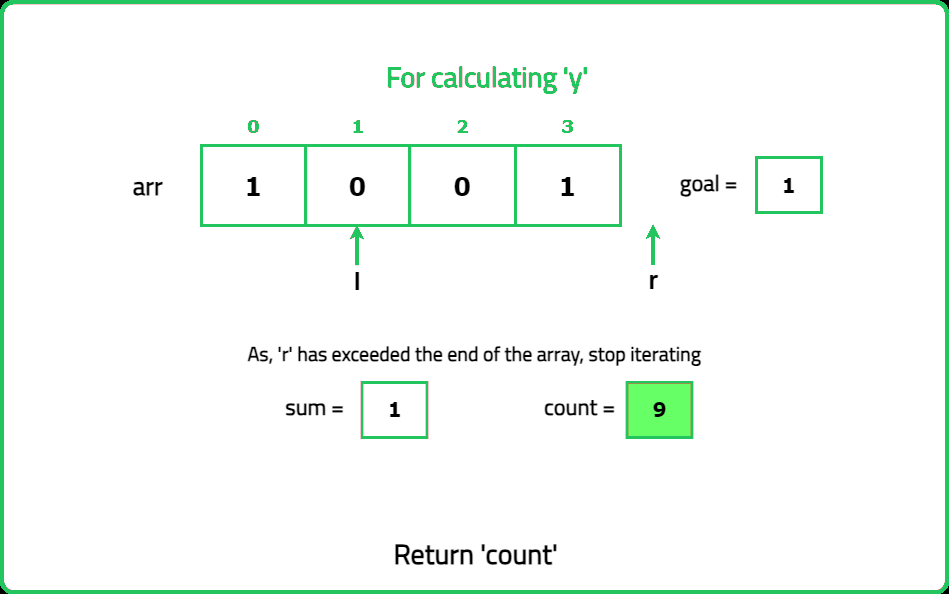
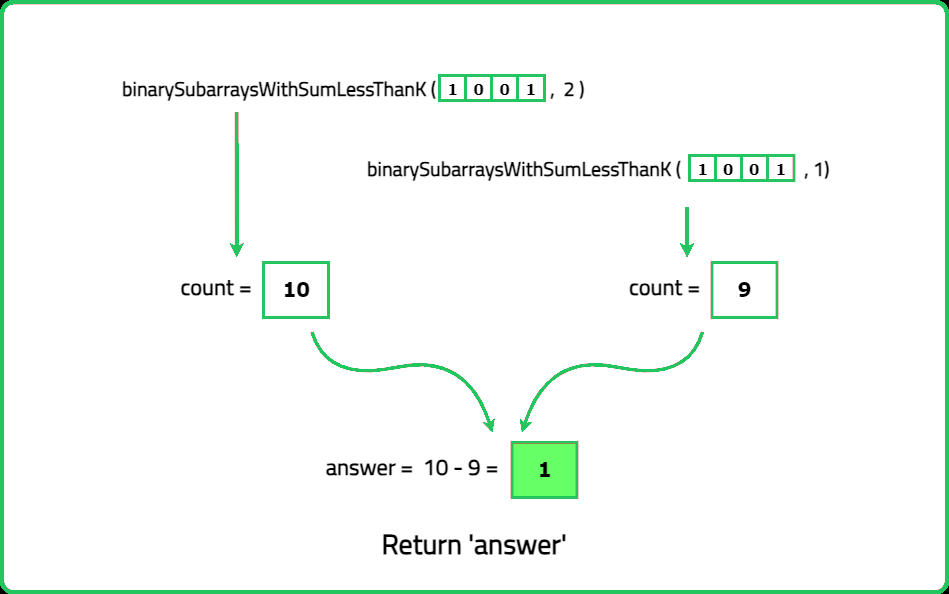
- Identify the positions of odd numbers in the array. Each "nice" subarray must contain exactly k odd numbers. Use a prefix sum or sliding window approach to count subarrays with exactly k odd numbers.
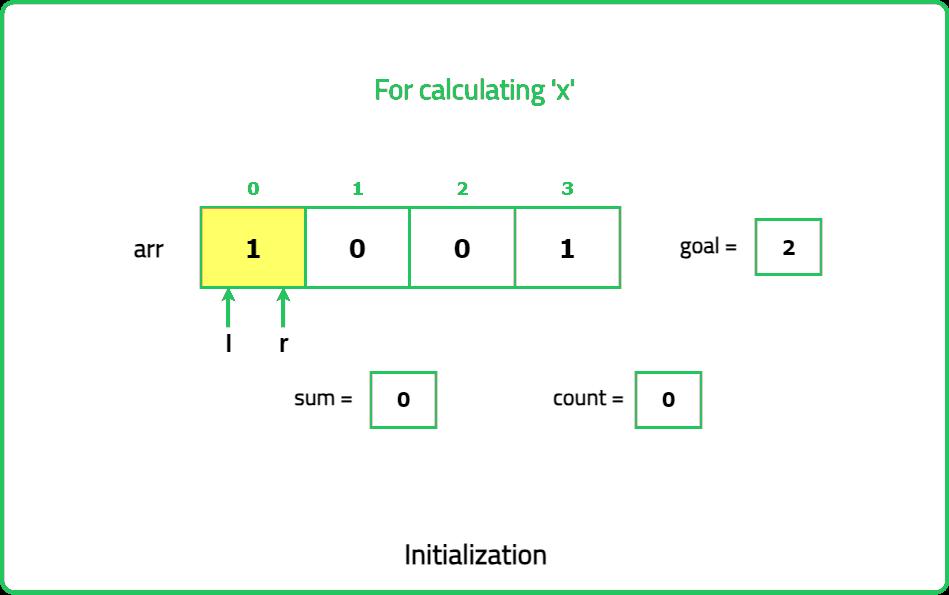
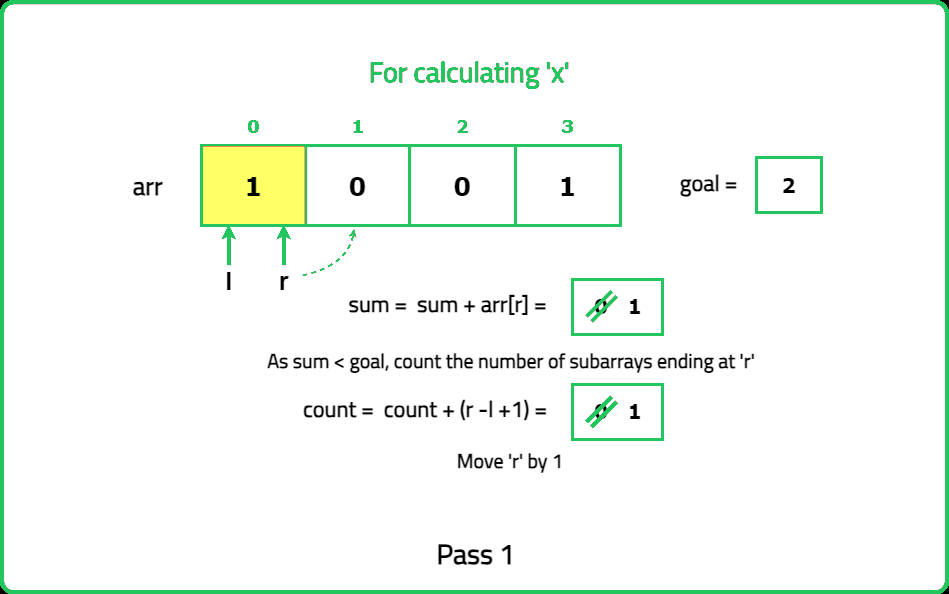
- Maintain two pointers (left and right) to define the current subarray. Expand the window by moving the right pointer until the subarray contains k odd numbers. Once the subarray contains k odd numbers, count all valid subarrays starting from the left pointer.
Company Tags
Activision Blizzard
Riot Games
Boston Consulting Group
Oracle
McKinsey & Company
Epic Games
Deloitte
IBM
Wayfair
GE Healthcare
Teladoc Health
Johnson & Johnson
Broadcom
AMD
Square
Salesforce
ARM
Micron Technology
Ubisoft
Unity Technologies
Target
DoorDash
Reddit
Chewy
HCL Technologies
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe