Wildcard matching
- This pattern matching problem forms the basis for one of the most essential functions in computer systems: file or text searching
- The most basic example is wildcard searches in operating systems
- In Windows, for instance, '?' is used to replace any single character and '*' is used to replace a string of character(s)
- Besides, Regular Expressions (regex), a common tool used in programming for string pattern searching and manipulation, also rely on this concept
- Regex is used extensively in programming from simple string manipulation, data validation, data scraping to more complicated natural language processing tasks
Given a string str and a pattern pat, implement a pattern matching function that supports the following special characters:
'?' Matches any single character.
'*' Matches any sequence of characters (including the empty sequence).
The pattern must match the entire string.
Examples:
Input: str = "xaylmz", pat = "x?y*z"
Output: true
Explanation:
The pattern "x?y*z" matches the string "xaylmz":
- '?' matches 'a'
- '*' matches "lm"
- 'z' matches 'z'
Input: str = "xyza", pat = "x*z"
Output: false
Explanation:
The pattern "x*z" does not match the string "xyza" because there is an extra 'a' at the end of the string that is not matched by the pattern.
Input: str = "abc", par = "a?c"
Constraints
- 1 <= length of(str, pattern) <= 200
Hints
- Define dp[i][j] as True if str[0:i] matches pat[0:j], otherwise False.
- "If pat[j-1] == str[i-1] or pat[j-1] == '?', dp[i][j]=dp[i−1][j−1] If pat[j-1] == '*', dp[i][j]=dp[i−1][j](use ‘*‘ as a sequence) OR dp[i][j−1](ignore ‘*‘) Otherwise, dp[i][j] = False."
Company Tags
Editorial
Understanding:
For every index of string S1, we have different options to match that index with string S2. Therefore, we can think in terms of string matching path as we have done already in previous questions.
- Either the characters match already.
- Or, if there is a ‘?’, we can explicitly match a single character.
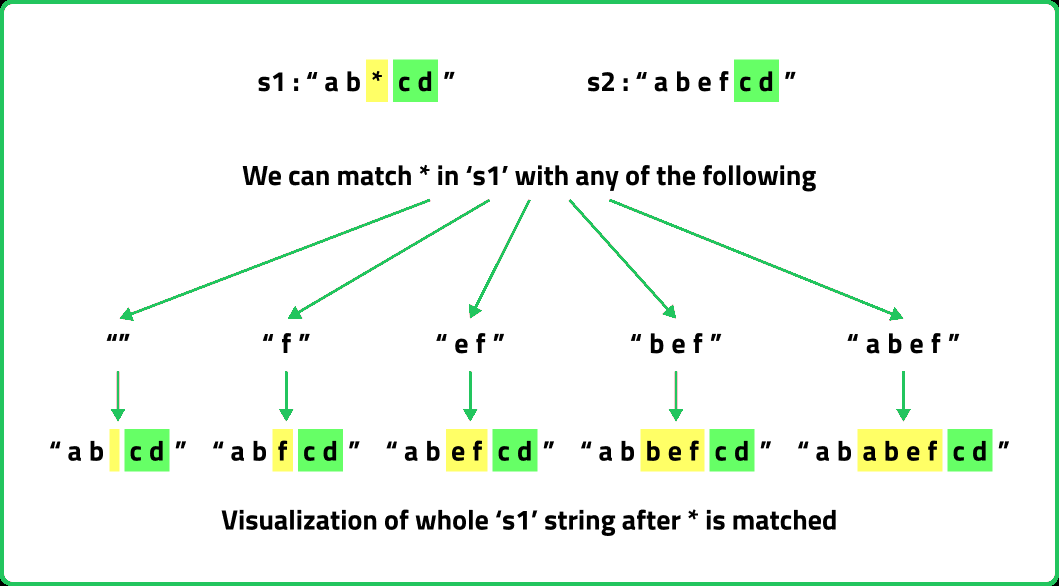
- For a ‘*’, the following figure explains the scenario.
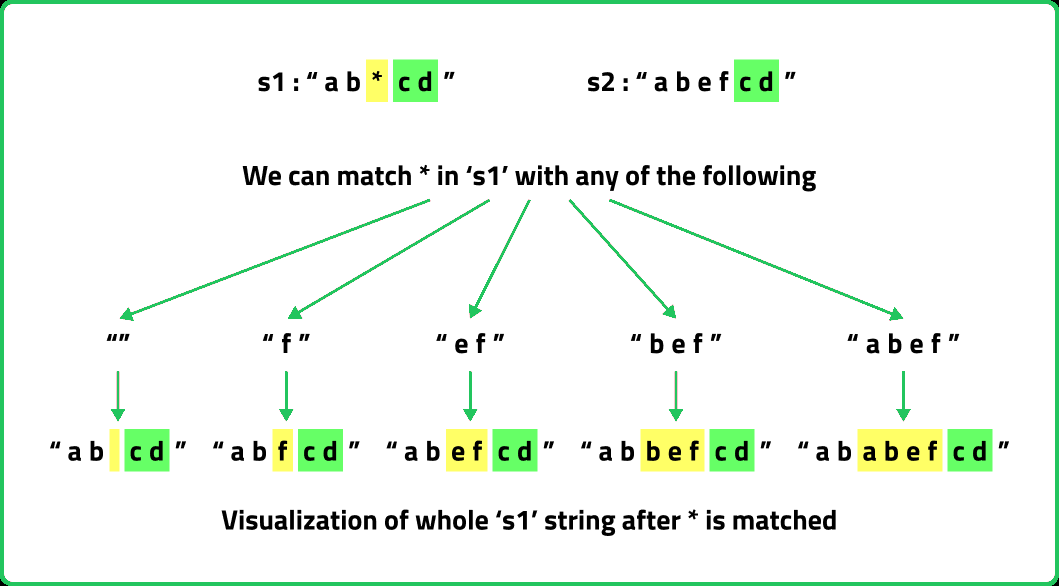
As there is no uniformity in data, there is no other way to find out than to try out all possible ways. To do so we will need to use recursion.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given two strings. We can represent them with the help of two indexes i and j. Initially, i=n-1 and j=m-1, where n and m are lengths of strings S1 and S2. Initially, we will call f(n-1,m-1), which means whether string S1[0…n-1] matches with string S2[0…m-1]. f(i, j) returns whether string S1[from index 0 to i] matches S2[from index 0 to j].
- Try out all possible choices at a given index:Now, i and j represent two characters from strings S1 and S2 respectively. There are only two options that make sense: either the characters represented by i and j match or they don’t.
- S1[i] == ‘?’: In this case, we can explicitly match ‘?’ at index i of S1 with the corresponding character at index j of S2. And then recursively call f(i-1,j-1) to check for the remaining string.
- S1[i] == ‘*’: This is an interesting case as now ‘*’ can be replaced with any sequence of characters( of length 0 or more) from S2.
- Call f(i-1,j). i.e replace ‘*’ with nothing and act as if it was not present.
- Call f(i,j-1). i.e replace ‘*’ with a single character at index j and make the i pointer to still point at index i. In this, we matched it with a single character (one of the many options that need to be tried) and in the next recursive call, as i still point to ‘*’, we get the exact two recursive calls again.
- If S1[i] is neither ‘?’ nor ‘*’: Then we can say as the characters at i and j don’t match then the strings don’t match, so we return false.
- If S1[i] == ‘?’, return f(i-1,j)
- Else if S1[i] == ‘*’, return f(i-1,j) || f(i,j-1)
- Else return false
- Return logical OR (||) of all the choices: If any of the cases return true, we can say that strings do match. We can use OR operator (||) with the recursive calls.
- Base Cases: We are reducing i and j in our recursive relation, there can be two possibilities, either i becomes -1 or j becomes -1., i,e we exhaust either S1 or S2 respectively.
- When S1 is exhausted: When S1 is exhausted (i<0), we know that in order for the strings to match, String S2 should also exhaust simultaneously. If it does, we return true, else we return false. We can say, if(i<0 && j<0), return true and if(i<0 && j>=0), return false.
- When S2 is exhausted: When S2 is exhausted(j<0) and S1 has not, there is only one pattern that can account for true(matching of strings). It is if S1 is like this “*”, ”****”, ”***”, i.e: S1 contains only stars. Then we can replace every star with a sequence of length 0 and say that the string match. If S1 is all-stars, we return true, else return false.
When the characters match: If(S1[i] == S2[j]), the characters at i and j match, we can simply move to the next characters of both the strings. So we will just decrement both i and j by 1 and recursively find the answer for the remaining string portions. We return f(i-1,j-1). The following figure makes it clear.
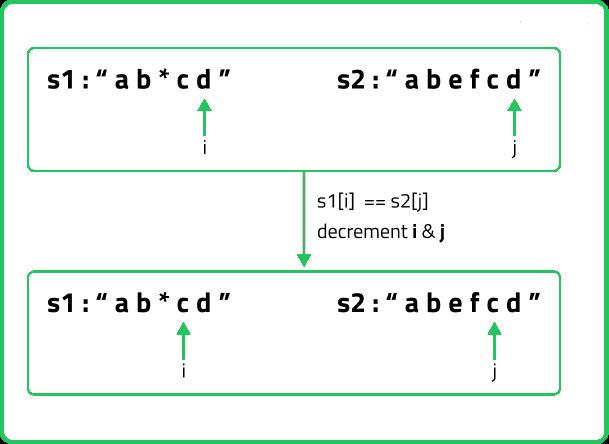
When the characters don’t match: If the characters don’t match, there are three possible scenarios:
If any of these cases return true, we can say that the characters do match. The next question is how to try all possible ways.
We are using two pointers i and j to represent characters of strings S1 and S2. We can surely write a for loop to compare characters from 0 to j of S2 for the above scenario. Can we do it more smartly? Yes, we can. Please understand the approach explained below.
We are using a recursive function f(i,j). If we do only the following two recursive calls:
The following recursive tree will help us to understand the recursion better:
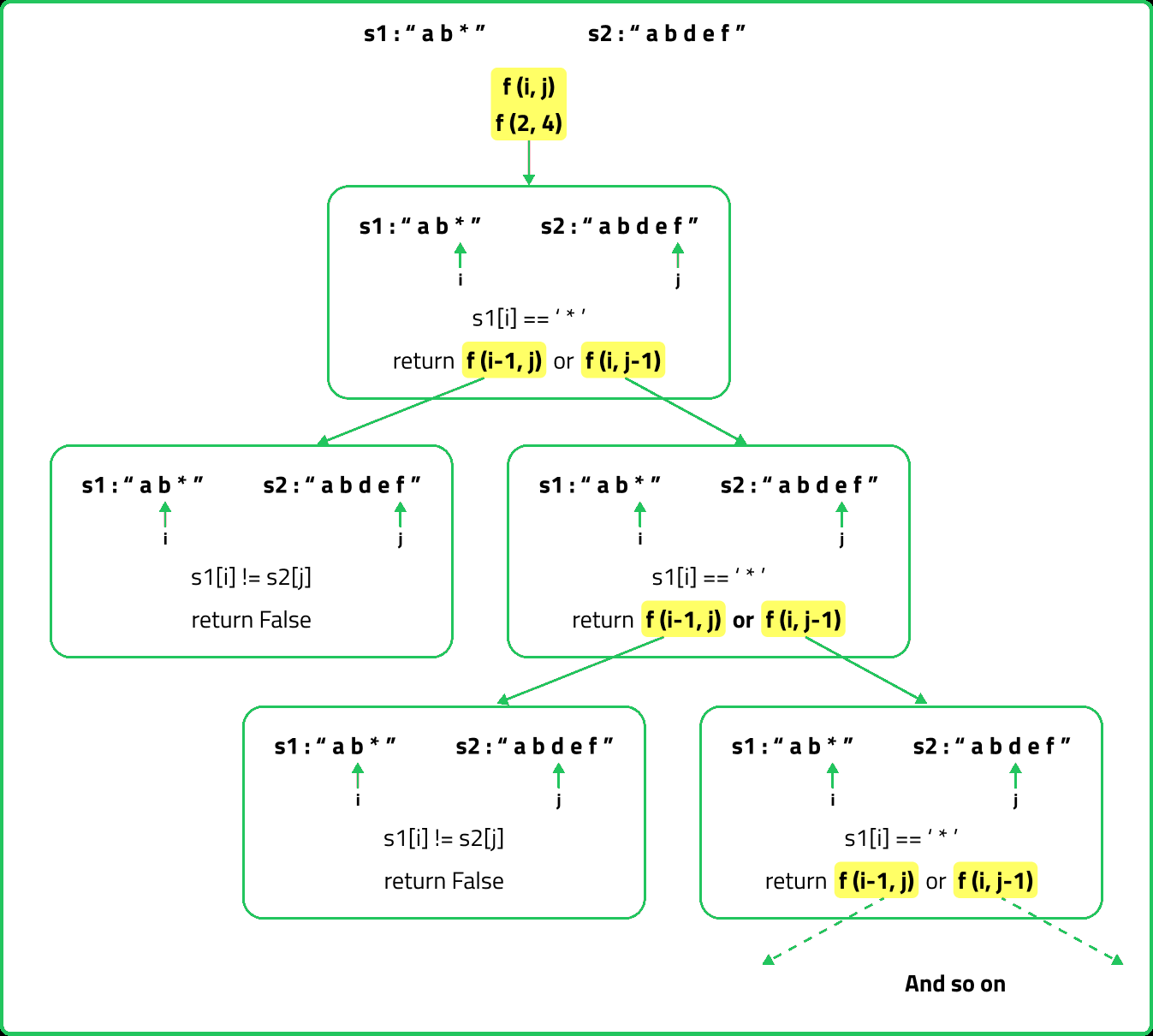
So we see how we can tackle all the required cases associated with ‘*’ by using recursion.
To summarise:
/*It is pseudocode and it is not related
to any specific programming language */
f(i, j){
if(S1[i] == S2[j] || S1[i] == '?'){
return f(i-1, j-1)
}
if(S1 == '*'){
return f(i-1, j) || f(i, j-1)
}
else
return false
}#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Function to check if a
substring of S1 contains only '*' */
bool isAllStars(string &S1, int i) {
for (int j = 0; j <= i; j++) {
if (S1[j] != '*')
return false;
}
return true;
}
/* Function to check if S1 matches
S2 using wildcard pattern matching*/
bool wildcardMatchingUtil(string &S1, string &S2, int i, int j) {
// Base Cases
if (i < 0 && j < 0)
return true;
if (i < 0 && j >= 0)
return false;
if (j < 0 && i >= 0)
return isAllStars(S1, i);
/* If the characters at the current
positions match or S1 has a '?'*/
if (S1[i] == S2[j] || S1[i] == '?'){
return wildcardMatchingUtil(S1, S2, i - 1, j - 1);
}
/* Two options: either '*' represents an
empty string or it matches a character in S2*/
if (S1[i] == '*'){
return wildcardMatchingUtil(S1, S2, i - 1, j) || wildcardMatchingUtil(S1, S2, i, j - 1);
}
return false;
}
public:
/* Function to check if 'Str' matches
'pat' using wildcard pattern matching*/
bool wildCard(string str, string pat) {
int n = str.size();
int m = pat.size();
return wildcardMatchingUtil(pat, str, m - 1, n - 1);
}
};
int main() {
string S1 = "ab*cd";
string S2 = "abdefcd";
//Create an instance of Solution class
Solution sol;
// Call wildcardMatching function and print the result
if (sol.wildcard(S1, S2))
cout << "String S1 and S2 do match";
else
cout << "String S1 and S2 do not match";
return 0;
}
public class Solution {
/* Function to check if a
substring of S1 contains only '*' */
private boolean isAllStars(String S1, int i) {
for (int j = 0; j <= i; j++) {
if (S1.charAt(j) != '*')
return false;
}
return true;
}
/* Function to check if S1 matches
S2 using wildcard pattern matching */
private boolean wildcardMatchingUtil(String S1, String S2, int i, int j) {
// Base Cases
if (i < 0 && j < 0)
return true;
if (i < 0 && j >= 0)
return false;
if (j < 0 && i >= 0)
return isAllStars(S1, i);
/* If the characters at the current
positions match or S1 has a '?' */
if (S1.charAt(i) == S2.charAt(j) || S1.charAt(i) == '?') {
return wildcardMatchingUtil(S1, S2, i - 1, j - 1);
}
/* Two options: either '*' represents an
empty string or it matches a character in S2 */
if (S1.charAt(i) == '*') {
return wildcardMatchingUtil(S1, S2, i - 1, j) || wildcardMatchingUtil(S1, S2, i, j - 1);
}
return false;
}
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
public boolean wildCard(String str, String pat) {
int n = str.length();
int m = pat.length();
return wildcardMatchingUtil(pat, str, m - 1, n - 1);
}
public static void main(String[] args) {
Solution sol = new Solution();
String str = "abc";
String pat = "a?c";
System.out.println(sol.wildCard(str, pat)); // Output: true
}
}
class Solution:
""" Function to check if a
substring of S1 contains only '*' """
def is_all_stars(self, S1, i):
for j in range(i + 1):
if S1[j] != '*':
return False
return True
""" Function to check if S1 matches
S2 using wildcard pattern matching"""
def wildcard_matching_util(self, S1, S2, i, j):
# Base Cases
if i < 0 and j < 0:
return True
if i < 0 and j >= 0:
return False
if j < 0 and i >= 0:
return self.is_all_stars(S1, i)
""" If the characters at the current
positions match or S1 has a '?'"""
if S1[i] == S2[j] or S1[i] == '?':
return self.wildcard_matching_util(S1, S2, i - 1, j - 1)
""" Two options: either '*' represents an
empty string or it matches a character in S2"""
if S1[i] == '*':
return self.wildcard_matching_util(S1, S2, i - 1, j) or self.wildcard_matching_util(S1, S2, i, j - 1)
return False
""" Function to check if 'Str' matches
'pat' using wildcard pattern matching"""
def wildCard(self, str, pat):
n = len(str)
m = len(pat)
return self.wildcard_matching_util(pat, str, m-1, n-1)
str = "abc"
pat = "a?c"
#Create an instance of Solution class
sol = Solution()
print(sol.wildCard(str, pat))
class Solution {
/* Function to check if a
substring of S1 contains only '*' */
isAllStars(S1, i) {
for (let j = 0; j <= i; j++) {
if (S1[j] !== '*')
return false;
}
return true;
}
/* Function to check if S1 matches
S2 using wildcard pattern matching */
wildcardMatchingUtil(S1, S2, i, j) {
// Base Cases
if (i < 0 && j < 0)
return true;
if (i < 0 && j >= 0)
return false;
if (j < 0 && i >= 0)
return this.isAllStars(S1, i);
/* If the characters at the current
positions match or S1 has a '?' */
if (S1[i] === S2[j] || S1[i] === '?') {
return this.wildcardMatchingUtil(S1, S2, i - 1, j - 1);
}
/* Two options: either '*' represents an
empty string or it matches a character in S2 */
if (S1[i] === '*') {
return this.wildcardMatchingUtil(S1, S2, i - 1, j) || this.wildcardMatchingUtil(S1, S2, i, j - 1);
}
return false;
}
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
wildCard(str, pat) {
const n = str.length;
const m = pat.length;
return this.wildcardMatchingUtil(pat, str, m-1, n-1);
}
}
const str = "abc";
const pat = "a?c";
//Create an instance of Solution class
const sol = new Solution();
console.log(sol.wildCard(str, pat));
Complexity Analysis:
Time Complexity: ExponentialSpace Complexity: O(N+M), we are using a stack space of N+M.
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
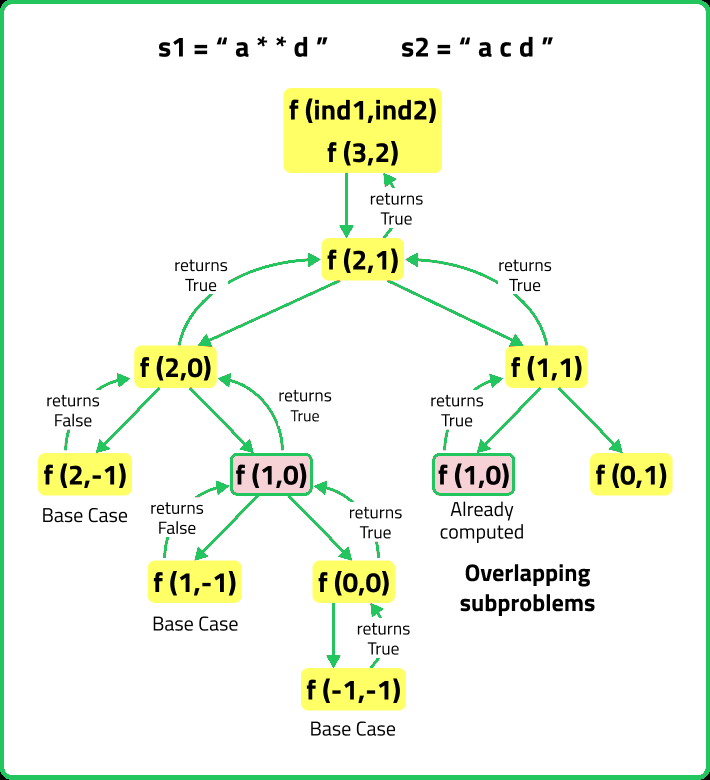
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][m]: As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' can attain is 'n-1', where n is the size of string S1 and 'j' can take maximum value of 'm-1', where m is the size of string S2. Therefore, we need 2D dp array.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to check if a
substring of S1 contains only '*'*/
bool isAllStars(string S1, int i) {
for (int j = 0; j <= i; j++) {
if (S1[j] != '*')
return false;
}
return true;
}
/* Function to check if S1 matches S2
using wildcard pattern matching*/
bool wildcardMatchingUtil(string S1, string S2, int i, int j, vector<vector<int>> &dp) {
// Base Cases
if (i < 0 && j < 0)
return true;
if (i < 0 && j >= 0)
return false;
if (j < 0 && i >= 0)
return isAllStars(S1, i);
/* If the result for this state has
already been calculated, return it*/
if (dp[i][j] != -1)
return dp[i][j] == 1;
//bool result;
/* If the characters at the current
positions match or S1 has a '?'*/
if (S1[i] == S2[j] || S1[i] == '?') {
return dp[i][j] = wildcardMatchingUtil(S1, S2, i - 1, j - 1, dp);
}
if (S1[i] == '*') {
/* Two options: either '*' represents an
empty string or it matches a character in S2*/
return dp[i][j] = wildcardMatchingUtil(S1, S2, i - 1, j, dp) || wildcardMatchingUtil(S1, S2, i, j - 1, dp);
} else {
return dp[i][j] = false;
}
}
public:
/* Function to check if 'str' matches
'pat' using wildcard pattern matching*/
bool wildCard(string str, string pat) {
int n = str.size();
int m = pat.size();
/* Create a DP table for
memoization, initialized with -1*/
vector<vector<int>> dp(m, vector<int>(n, -1));
return wildcardMatchingUtil(pat, str, m-1, n-1, dp);
}
};
int main() {
string S1 = "ab*cd";
string S2 = "abdefcd";
//Create an instance of Solution class
Solution sol;
// Call wildcardMatching function and print the result
if (sol.wildCard(S1, S2))
cout << "String S1 and S2 do match";
else
cout << "String S1 and S2 do not match";
return 0;
}
import java.util.*;
class Solution {
/* Function to check if a
substring of S1 contains only '*' */
private boolean isAllStars(String S1, int i) {
for (int j = 0; j <= i; j++) {
if (S1.charAt(j) != '*')
return false;
}
return true;
}
/* Function to check if S1 matches
S2 using wildcard pattern matching */
private boolean wildcardMatchingUtil(String S1, String S2, int i, int j, int[][] dp) {
// Base Cases
if (i < 0 && j < 0)
return true;
if (i < 0 && j >= 0)
return false;
if (j < 0 && i >= 0)
return isAllStars(S1, i);
/* If the result for this state has
already been calculated, return it */
if (dp[i][j] != -1)
return dp[i][j] == 1;
boolean result;
/* If the characters at the current
positions match or S1 has a '?' */
if (S1.charAt(i) == S2.charAt(j) || S1.charAt(i) == '?') {
result = wildcardMatchingUtil(S1, S2, i - 1, j - 1, dp);
} else if (S1.charAt(i) == '*') {
/* Two options: either '*' represents an
empty string or it matches a character in S2 */
result = wildcardMatchingUtil(S1, S2, i - 1, j, dp) || wildcardMatchingUtil(S1, S2, i, j - 1, dp);
} else {
result = false;
}
/* Memoize the result */
dp[i][j] = result ? 1 : 0;
return result;
}
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
public boolean wildCard(String str, String pat) {
int n = str.length();
int m = pat.length();
/* Create a DP table for
memoization, initialized with -1 */
int[][] dp = new int[m][n];
for (int[] row : dp) {
Arrays.fill(row, -1);
}
return wildcardMatchingUtil(pat, str, m-1, n-1, dp);
}
public static void main(String[] args) {
String S1 = "ab*cd";
String S2 = "abdefcd";
// Create an instance of Solution class
Solution sol = new Solution();
// Call wildCard function and print the result
if (sol.wildCard(S1, S2))
System.out.println("String S1 and S2 do match");
else
System.out.println("String S1 and S2 do not match");
}
}
class Solution:
""" Function to check if a
substring of S1 contains only '*'"""
def isAllStars(self, S1, i):
for j in range(i + 1):
if S1[j] != '*':
return False
return True
""" Function to check if S1 matches
S2 using wildcard pattern matching"""
def wildcardMatchingUtil(self, S1, S2, i, j, dp):
# Base Cases
if i < 0 and j < 0:
return True
if i < 0 and j >= 0:
return False
if j < 0 and i >= 0:
return self.isAllStars(S1, i)
""" If the result for this state has
already been calculated, return it"""
if dp[i][j] != -1:
return dp[i][j] == 1
""" If the characters at the current
positions match or S1 has a '?'"""
if S1[i] == S2[j] or S1[i] == '?':
result = self.wildcardMatchingUtil(S1, S2, i - 1, j - 1, dp)
elif S1[i] == '*':
""" Two options: either '*' represents an
empty string or it matches a character in S2"""
result = self.wildcardMatchingUtil(S1, S2, i - 1, j, dp) or self.wildcardMatchingUtil(S1, S2, i, j - 1, dp)
else:
result = False
# Memoize the result
dp[i][j] = 1 if result else 0
return result
""" Function to check if 'str' matches
'pat' using wildcard pattern matching"""
def wildCard(self, str, pat):
n = len(str)
m = len(pat)
""" Create a DP table for
memoization, initialized with -1"""
dp = [[-1 for _ in range(n)] for _ in range(m)]
return self.wildcardMatchingUtil(pat, str, m-1, n-1, dp)
S1 = "ab*cd"
S2 = "abdefcd"
# Create an instance of Solution class
sol = Solution()
# Call wildCard function and print the result
if sol.wildCard(S1, S2):
print("String S1 and S2 do match")
else:
print("String S1 and S2 do not match")
class Solution {
/* Function to check if a
substring of S1 contains only '*'*/
isAllStars(S1, i) {
for (let j = 0; j <= i; j++) {
if (S1[j] !== '*')
return false;
}
return true;
}
/* Function to check if S1 matches
S2 using wildcard pattern matching*/
wildcardMatchingUtil(S1, S2, i, j, dp) {
// Base Cases
if (i < 0 && j < 0)
return true;
if (i < 0 && j >= 0)
return false;
if (j < 0 && i >= 0)
return this.isAllStars(S1, i);
/* If the result for this state has
already been calculated, return it*/
if (dp[i][j] !== -1)
return dp[i][j] === 1;
let result;
/* If the characters at the current
positions match or S1 has a '?'*/
if (S1[i] === S2[j] || S1[i] === '?') {
result = this.wildcardMatchingUtil(S1, S2, i - 1, j - 1, dp);
} else if (S1[i] === '*') {
/* Two options: either '*' represents an
empty string or it matches a character in S2*/
result = this.wildcardMatchingUtil(S1, S2, i - 1, j, dp) || this.wildcardMatchingUtil(S1, S2, i, j - 1, dp);
} else {
result = false;
}
// Memoize the result
dp[i][j] = result ? 1 : 0;
return result;
}
/* Function to check if 'str' matches
'pat' using wildcard pattern matching*/
wildCard(str, pat) {
const n = str.length;
const m = pat.length;
/* Create a DP table for
memoization, initialized with -1*/
const dp = Array.from({ length: m }, () => Array(n).fill(-1));
return this.wildcardMatchingUtil(pat, str, m-1, n-1, dp);
}
}
const S1 = "ab*cd";
const S2 = "abdefcd";
// Create an instance of Solution class
const sol = new Solution();
// Call wildCard function and print the result
if (sol.wildCard(S1, S2)) {
console.log("String S1 and S2 do match");
} else {
console.log("String S1 and S2 do not match");
}
Complexity Analysis:
Time Complexity: O(N*M), Where N is the length of string S1 and M is the length of string S2. There are N*M states therefore at max ‘N*M’ new problems will be solved.Space Complexity: O(N*M) + O(N+M), We are using a recursion stack space(O(N+M)) and a 2D array (O(N*M)).
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- In the recursive logic, we set the base case too if(i<0 ) and if(j<0) but we can’t set the dp array’s index to -1. Therefore a hack for this issue is to shift every index by 1 towards the right.
- Declare a dp array of size [n+1][m+1]: As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' can attain is 'n+1', where n is the size of string S1 and 'j' can take maximum value of 'm+1', where m is the size of string S2. Therefore, we need 2D dp array. Initialize the array as zero.
- Setting Base Cases in the Array: Set the base condition (keep in mind 1-based indexing), we set the top-left cell as ‘true’, then we set the first column’s value as ‘false’; and for the first row, we will run isAllStars() for every cell value.
- Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. By keeping in mind the shifting of indexes, therefore S1[i] will be converted to S1[i-1]. Same for S2.
- Returning the answer: At last dp[n][m] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
bool wildCard(string str, string pat) {
int n = str.size();
int m = pat.size();
/* Create a DP table for
memoization, initialized with false */
vector<vector<bool>> dp(n + 1, vector<bool>(m + 1, false));
dp[0][0] = true;
// Initialize the first row
for (int j = 1; j <= m; j++) {
dp[0][j] = (pat[j - 1] == '*') && dp[0][j - 1];
}
// Initialize the first column
for (int i = 1; i <= n; i++) {
bool flag = true;
for (int ii = 1; ii <= i; ii++) {
if (str[ii - 1] != '*') {
flag = false;
break;
}
}
dp[i][0] = flag;
}
// Fill the DP table
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
/* If the characters at the current
positions match or str has a '?' */
if (str[i - 1] == pat[j - 1] || str[i - 1] == '?') {
dp[i][j] = dp[i - 1][j - 1];
} else if (str[i - 1] == '*') {
/* Two options: either '*' represents an
empty string or it matches a character in pat */
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
} else {
dp[i][j] = false;
}
}
}
return dp[n][m];
}
};
int main() {
string S1 = "ab*cd";
string S2 = "abdefcd";
// Create an instance of Solution class
Solution sol;
// Call wildCard function and print the result
if (sol.wildCard(S1, S2))
cout << "String S1 and S2 do match";
else
cout << "String S1 and S2 do not match";
return 0;
}
import java.util.*;
class Solution {
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
public boolean wildCard(String str, String pat) {
int n = str.length();
int m = pat.length();
/* Create a DP table for
memoization, initialized with false */
boolean[][] dp = new boolean[n + 1][m + 1];
dp[0][0] = true;
// Initialize the first row
for (int j = 1; j <= m; j++) {
dp[0][j] = (pat.charAt(j - 1) == '*') && dp[0][j - 1];
}
// Initialize the first column
for (int i = 1; i <= n; i++) {
boolean flag = true;
for (int ii = 1; ii <= i; ii++) {
if (str.charAt(ii - 1) != '*') {
flag = false;
break;
}
}
dp[i][0] = flag;
}
// Fill the DP table
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
/* If the characters at the current
positions match or str has a '?' */
if (str.charAt(i - 1) == pat.charAt(j - 1) || str.charAt(i - 1) == '?') {
dp[i][j] = dp[i - 1][j - 1];
} else if (str.charAt(i - 1) == '*') {
/* Two options: either '*' represents an
empty string or it matches a character in pat */
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
} else {
dp[i][j] = false;
}
}
}
return dp[n][m];
}
}
public class Main {
public static void main(String[] args) {
String S1 = "ab*cd";
String S2 = "abdefcd";
// Create an instance of Solution class
Solution sol = new Solution();
// Call wildCard function and print the result
if (sol.wildCard(S1, S2))
System.out.println("String S1 and S2 do match");
else
System.out.println("String S1 and S2 do not match");
}
}
class Solution:
""" Function to check if 'str' matches
'pat' using wildcard pattern matching"""
def wildCard(self, str, pat):
n = len(str)
m = len(pat)
""" Create a DP table for memoization,
initialized with False"""
dp = [[False] * (m + 1) for _ in range(n + 1)]
dp[0][0] = True
# Initialize the first row
for j in range(1, m + 1):
dp[0][j] = (pat[j - 1] == '*') and dp[0][j - 1]
# Initialize the first column
for i in range(1, n + 1):
flag = True
for ii in range(1, i + 1):
if str[ii - 1] != '*':
flag = False
break
dp[i][0] = flag
# Fill the DP table
for i in range(1, n + 1):
for j in range(1, m + 1):
""" If the characters at the current
positions match or str has a '?'"""
if str[i - 1] == pat[j - 1] or str[i - 1] == '?':
dp[i][j] = dp[i - 1][j - 1]
elif str[i - 1] == '*':
""" Two options: either '*' represents an
empty string or it matches a character in pat"""
dp[i][j] = dp[i - 1][j] or dp[i][j - 1]
else:
dp[i][j] = False
return dp[n][m]
if __name__ == "__main__":
S1 = "ab*cd"
S2 = "abdefcd"
# Create an instance of Solution class
sol = Solution()
# Call wildCard function and print the result
if sol.wildCard(S1, S2):
print("String S1 and S2 do match")
else:
print("String S1 and S2 do not match")
class Solution {
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
wildCard(str, pat) {
const n = str.length;
const m = pat.length;
/* Create a DP table for
memoization, initialized with false */
const dp = Array.from({ length: n + 1 }, () => Array(m + 1).fill(false));
dp[0][0] = true;
// Initialize the first row
for (let j = 1; j <= m; j++) {
dp[0][j] = (pat[j - 1] === '*') && dp[0][j - 1];
}
// Initialize the first column
for (let i = 1; i <= n; i++) {
let flag = true;
for (let ii = 1; ii <= i; ii++) {
if (str[ii - 1] !== '*') {
flag = false;
break;
}
}
dp[i][0] = flag;
}
// Fill the DP table
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
/* If the characters at the current
positions match or str has a '?' */
if (str[i - 1] === pat[j - 1] || str[i - 1] === '?') {
dp[i][j] = dp[i - 1][j - 1];
} else if (str[i - 1] === '*') {
/* Two options: either '*' represents an
empty string or it matches a character in pat */
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
} else {
dp[i][j] = false;
}
}
}
return dp[n][m];
}
}
const main = () => {
const S1 = "ab*cd";
const S2 = "abdefcd";
// Create an instance of Solution class
const sol = new Solution();
// Call wildCard function and print the result
if (sol.wildCard(S1, S2))
console.log("String S1 and S2 do match");
else
console.log("String S1 and S2 do not match");
}
main();
Complexity Analysis:
Time Complexity: O(N*M), Where N is the length of string S1 and M is the length of string S2. As two nested loops are used, which runs for N*M times.Space Complexity: O(N*M), As 2D array N*M is used.
If we observe the relation obtained in the tabulation, dp[ind][target] = dp[ind-1][target] || dp[ind-1][target-arr[ind]]. We see that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it.
Steps to space optimize the tabulation approach:
- Decalre an array to store the previous row of the DP table. Initialize the first row and first column of the DP table based on the base conditions discussed in tabulation.
- Now, initiate two nested loops in bottom-up approach. The first loop will run for 'ind' and the second loop will run for the 'target' variable.
- In order to store the current row of the DP table, initialize a new array 'cur' and fill the first cell to 'true' for base condition.
- Do the calculations for 'cur' row by performing the pick/non-pick technique used in previous approaches.
- Now, update the previous row with the current row for the next iteration and at last return the final result stored in the last cell of the previous row(prev[k]).
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
bool wildCard(string str, string pat) {
int n = str.size();
int m = pat.size();
/* Create two arrays to store previous
and current rows of matching results*/
vector<bool> prev(m + 1, false);
vector<bool> cur(m + 1, false);
/* Initialize the first element
of the previous row to true*/
prev[0] = true;
// Initialize the first column
for (int i = 1; i <= n; i++) {
bool flag = true;
for (int ii = 1; ii <= i; ii++) {
if (str[ii - 1] != '*') {
flag = false;
break;
}
}
cur[0] = flag;
for (int j = 1; j <= m; j++) {
/* If the characters at the current
positions match or str has a '?' */
if (str[i - 1] == pat[j - 1] || str[i - 1] == '?') {
cur[j] = prev[j - 1];
}
else if (str[i - 1] == '*') {
/* Two options: either '*' represents an
empty string or it matches a character in pat */
cur[j] = prev[j] || cur[j - 1];
} else {
cur[j] = false;
}
}
prev = cur;
}
//Return the result
return prev[m];
}
};
int main() {
string S1 = "ab*cd";
string S2 = "abdefcd";
// Create an instance of Solution class
Solution sol;
// Call wildCard function and print the result
if (sol.wildCard(S1, S2))
cout << "String S1 and S2 do match";
else
cout << "String S1 and S2 do not match";
return 0;
}
import java.util.*;
class Solution {
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
public boolean wildCard(String str, String pat) {
int n = str.length();
int m = pat.length();
/* Create two arrays to store previous
and current rows of matching results */
boolean[] prev = new boolean[m + 1];
boolean[] cur = new boolean[m + 1];
/* Initialize the first element
of the previous row to true */
prev[0] = true;
// Initialize the first column
for (int i = 1; i <= n; i++) {
boolean flag = true;
for (int ii = 1; ii <= i; ii++) {
if (str.charAt(ii - 1) != '*') {
flag = false;
break;
}
}
cur[0] = flag;
for (int j = 1; j <= m; j++) {
/* If the characters at the current
positions match or str has a '?' */
if (str.charAt(i - 1) == pat.charAt(j - 1) || str.charAt(i - 1) == '?') {
cur[j] = prev[j - 1];
}
else if (str.charAt(i - 1) == '*') {
/* Two options: either '*' represents an
empty string or it matches a character in pat */
cur[j] = prev[j] || cur[j - 1];
} else {
cur[j] = false;
}
}
prev = Arrays.copyOf(cur, m + 1);
}
// Return the result
return prev[m];
}
public static void main(String[] args) {
String S1 = "ab*cd";
String S2 = "abdefcd";
// Create an instance of Solution class
Solution sol = new Solution();
// Call wildCard function and print the result
if (sol.wildCard(S1, S2))
System.out.println("String S1 and S2 do match");
else
System.out.println("String S1 and S2 do not match");
}
}
class Solution:
""" Function to check if 'str' matches
'pat' using wildcard pattern matching"""
def wildCard(self, str, pat):
n = len(str)
m = len(pat)
""" Create two arrays to store previous
and current rows of matching results"""
prev = [False] * (m + 1)
cur = [False] * (m + 1)
""" Initialize the first element
of the previous row to true"""
prev[0] = True
# Initialize the first column
for i in range(1, n + 1):
flag = True
for ii in range(1, i + 1):
if str[ii - 1] != '*':
flag = False
break
cur[0] = flag
for j in range(1, m + 1):
""" If the characters at the current
positions match or str has a '?'"""
if str[i - 1] == pat[j - 1] or str[i - 1] == '?':
cur[j] = prev[j - 1]
elif str[i - 1] == '*':
""" Two options: either '*' represents an
empty string or it matches a character in pat"""
cur[j] = prev[j] or cur[j - 1]
else:
cur[j] = False
prev = cur[:]
# Return the result
return prev[m]
if __name__ == "__main__":
S1 = "ab*cd"
S2 = "abdefcd"
# Create an instance of Solution class
sol = Solution()
# Call wildCard function and print the result
if sol.wildCard(S1, S2):
print("String S1 and S2 do match")
else:
print("String S1 and S2 do not match")
class Solution {
/* Function to check if 'str' matches
'pat' using wildcard pattern matching */
wildCard(str, pat) {
const n = str.length;
const m = pat.length;
/* Create two arrays to store previous
and current rows of matching results*/
const prev = new Array(m + 1).fill(false);
const cur = new Array(m + 1).fill(false);
/* Initialize the first element
of the previous row to true*/
prev[0] = true;
// Initialize the first column
for (let i = 1; i <= n; i++) {
let flag = true;
for (let ii = 1; ii <= i; ii++) {
if (str[ii - 1] !== '*') {
flag = false;
break;
}
}
cur[0] = flag;
for (let j = 1; j <= m; j++) {
/* If the characters at the current
positions match or str has a '?'*/
if (str[i - 1] === pat[j - 1] || str[i - 1] === '?') {
cur[j] = prev[j - 1];
} else if (str[i - 1] === '*') {
/* Two options: either '*' represents an
empty string or it matches a character in pat*/
cur[j] = prev[j] || cur[j - 1];
} else {
cur[j] = false;
}
}
for (let j = 0; j <= m; j++) {
prev[j] = cur[j];
}
}
// Return the result
return prev[m];
}
}
const S1 = "ab*cd";
const S2 = "abdefcd";
// Create an instance of Solution class
const sol = new Solution();
// Call wildCard function and print the result
if (sol.wildCard(S1, S2)) {
console.log("String S1 and S2 do match");
} else {
console.log("String S1 and S2 do not match");
}
Complexity Analysis:
Time Complexity: O(N*M), Where N is the length of string S1 and M is the length of string S2. As two nested loops are used, which runs for N*M times.Space Complexity: O(M), As array of size M+1 is used.
Frequently Occurring Doubts
Q: Why do we check dp[i-1][j] and dp[i][j-1] when pat[j-1] == '*'?
A: dp[i-1][j] → Considers * as matching one or more characters. dp[i][j-1] → Considers * as matching zero characters.
Q: Can we optimize space from O(n × m) to O(m)?
A: Yes! Since dp[i][j] only depends on the previous row, we use rolling arrays (prev[] and curr[]), reducing space to O(m).
Interview Followup Questions
Q: How would you modify this problem to return the actual matched substrings instead of just True/False?
A: Maintain a parent pointer while computing dp[], then backtrack to extract the matching substrings.
Q: How does this relate to the Regular Expression Matching problem?
A: Regular Expression Matching allows . (single character match) and * (previous character match multiple times), while this problem allows ? (single character) and * (any sequence).
Notes
Code
1
0
1