Divide two numbers without multiplication and division
Bit Manipulation
Problems
Medium
- Fun Fact: The concept of this problem can be encountered when you are working with systems that handle very large numbers, or when you are working with systems where the traditional division operation is either extremely costly in terms of performance or unavailable for certain data types
- For example, Big Data processing libraries such as Apache Hadoop and Apache Spark handle terabytes of data where conventional division may lead to precision errors or performance bottlenecks
- In such cases, using alternatives like bit manipulation – which is the deep-rooted concept in this problem – can help optimize performance
- Similarly, cryptographic algorithms and low-level hardware programming often require such unconventional methods to carry out basic operations
Given the two integers, dividend and divisor. Divide without using the mod, division, or multiplication operators and return the quotient.
The fractional portion of the integer division should be lost as it truncates toward zero.
As an illustration, 8.345 and -2.7335 would be reduced to 8 and -2 respectively.
Examples:
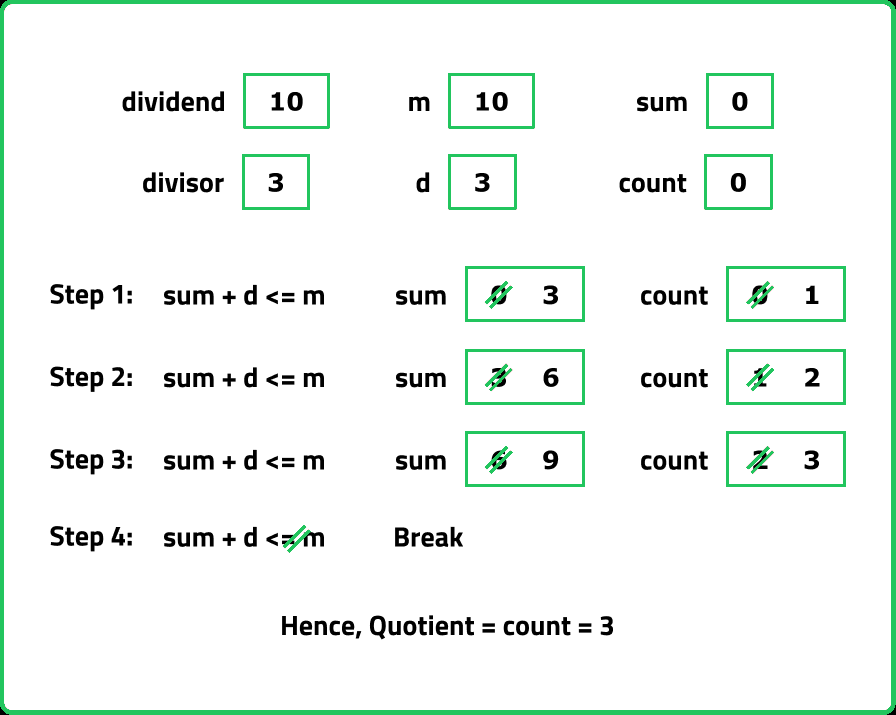
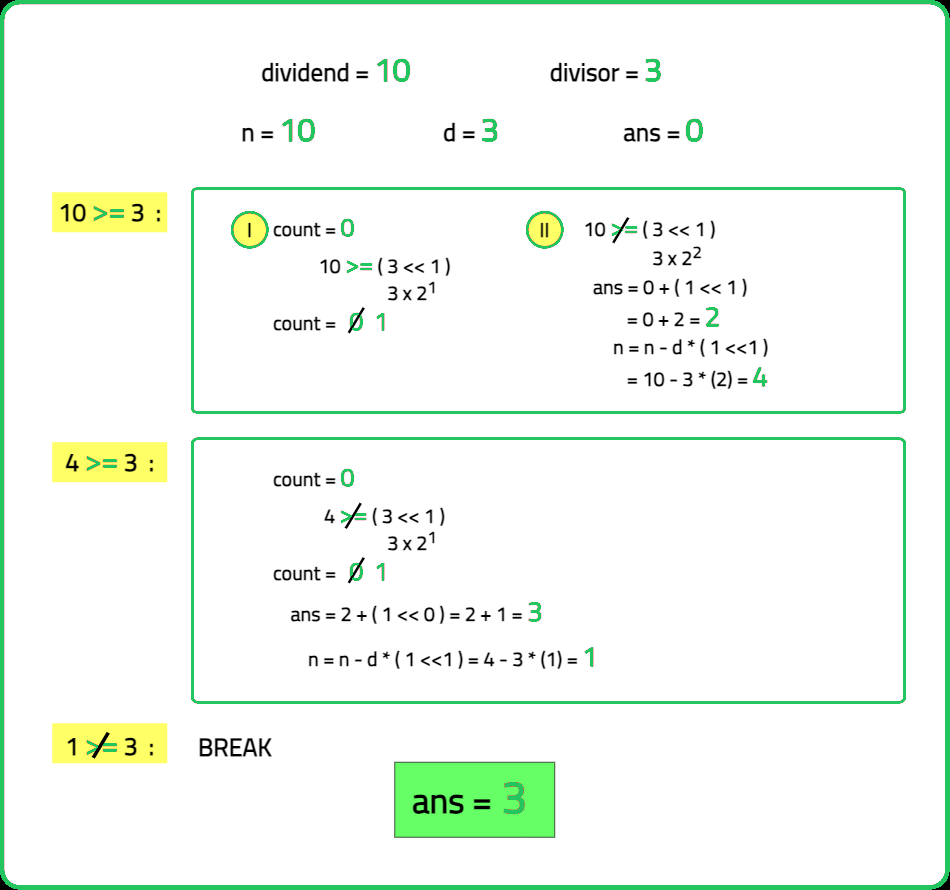
Input : Dividend = 10 , Divisor = 3
Output : 3
Explanation : 10/3 = 3.33 , truncated to 3.
Input : Dividend = 7 , Divisor = -3
Output : -2
Explanation : 7/-3 = -2.33 , truncated to -2.
Input : Dividend = 7 , Divisor = 2
Constraints
- -231 < dividend , divisor <= 231 - 1
- divisor != 0
Hints
- Instead of repeatedly subtracting the divisor, double its value using bitwise left shifts (divisor << k). Determine the largest multiple of the divisor that can be subtracted from the dividend without making it negative. Subtract this value and repeat until the remainder is less than the divisor.
- Determine the sign of the result by checking if the dividend and divisor have the same sign. Use sign = 1 if they do, otherwise sign = -1. Convert both numbers to their absolute values for computation.
Company Tags
Seagate Technology
Qualcomm
Optum
Activision Blizzard
Dropbox
Medtronic
Swiggy
Philips Healthcare
GE Healthcare
Instacart
Databricks
Epic Games
Shopify
PwC
Bloomberg
Nutanix
McKinsey & Company
Etsy
Wayfair
HashiCorp
Zynga
Salesforce
Deloitte
Bain & Company
JPMorgan Chase
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe