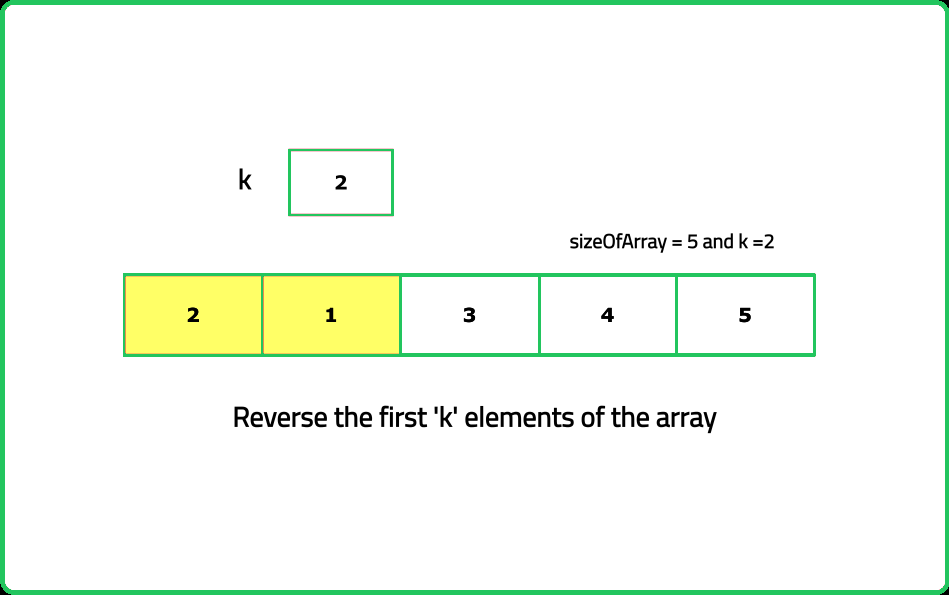
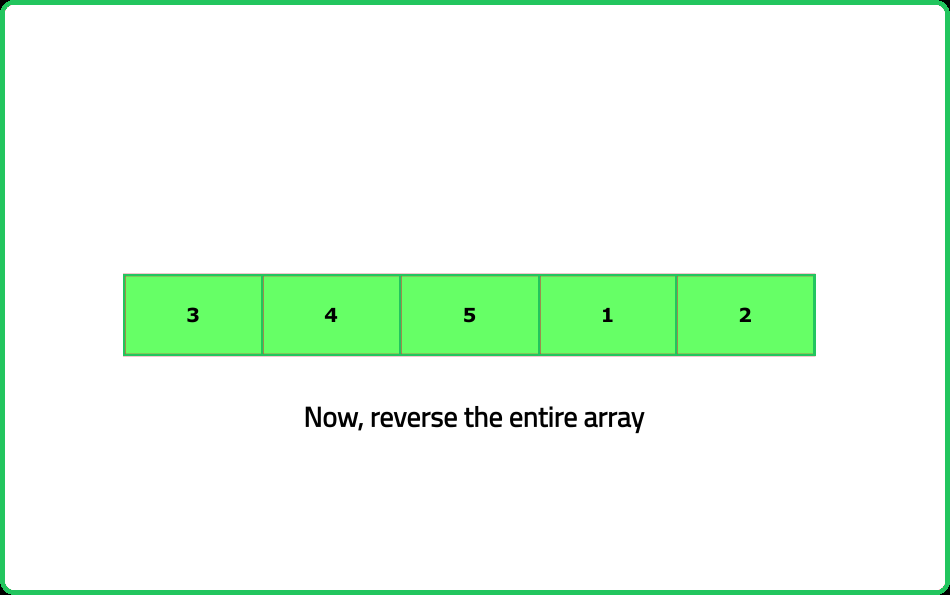
Left Rotate Array by K Places

Arrays Fundamentals Easy Go Ad-Free - ₹20/mo

Given an integer array nums and a non-negative integer k, rotate the array to the left by k steps.

Examples:

Input: nums = [1, 2, 3, 4, 5, 6], k = 2

Output: nums = [3, 4, 5, 6, 1, 2]

Explanation: rotate 1 step to the left: [2, 3, 4, 5, 6, 1]

rotate 2 steps to the left: [3, 4, 5, 6, 1, 2]

Input: nums = [3, 4, 1, 5, 3, -5], k = 8

Output: nums = [1, 5, 3, -5, 3, 4]

Explanation: rotate 1 step to the left: [4, 1, 5, 3, -5, 3]

rotate 2 steps to the left: [1, 5, 3, -5, 3, 4]

rotate 3 steps to the left: [5, 3, -5, 3, 4, 1]

rotate 4 steps to the left: [3, -5, 3, 4, 1, 5]

rotate 5 steps to the left: [-5, 3, 4, 1, 5, 3]

rotate 6 steps to the left: [3, 4, 1, 5, 3, -5]

rotate 7 steps to the left: [4, 1, 5, 3, -5, 3]

rotate 8 steps to the left: [1, 5, 3, -5, 3, 4]

Input: nums = [1, 2, 3, 4, 5], k = 4

Constraints

1 <= nums.length <= 10⁵
-10⁴ <= nums[i] <= 10⁴
0 <= k <= 10⁵

Hints

Split the array into two parts at index k: the first k elements and the rest. Then rearrange the two parts to place the second part before the first part.
Think about how you can achieve the rotation by reversing parts of the array rather than using extra space.

Company Tags

Reddit Docker Byju's Twilio Johnson & Johnson JPMorgan Chase Visa Shopify HashiCorp Flipkart Siemens Healthineers Teladoc Health Cerner Western Digital KPMG Goldman Sachs AMD Ubisoft McKinsey & Company Mastercard Oracle Robinhood Cloudflare Optum Roche TCS Cognizant Accenture Infosys Capgemini Wipro

Editorial

Intuition

The most optimal solution works based on the properties of reversing sections of the array. This involves reversing different parts of the array to achieve the desired rotation.

Why does this solution work?

Reversal Property: Reversing a segment of the array changes the order but keeps the elements intact. By reversing the segments first and then the entire array, you rearrange the elements correctly without needing extra space.

Maintaining Order: Each reversal step preserves the order of the elements within that segment, ensuring the elements that need to stay together remain so.

Approach

Reverse the first k elements of the array.

On reversing the first k elements, you are essentially reversing the order of the elements that will be moved to the back of the array. This prepares them to be placed at the end after the rotation.

Reverse the last N - K elements of the array.

Reversing the remaining elements (from position k to the end of the array) ensures that these elements maintain their relative order after the rotation. They will come before the first k elements in the final arrangement.

Reverse the entire array.

Finally, on reversal of the entire array, it combines the two previously reversed sections into the correct order. The first k elements (which were reversed first) are now at the end, and the last n-k elements (which were reversed second) are at the front, effectively achieving the left rotation.

Dry Run

Solution

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to rotate the array to the left by k positions
    void rotateArray(vector<int>& nums, int k) {
        int n = nums.size(); // Size of array
        k = k % n; // To avoid unnecessary rotations
        
        vector<int> temp;
        
        // Store first k elements in a temporary array
        for(int i=0; i < k; i++) {
            temp.push_back(nums[i]);
        }
        
        // Shift n-k elements of given array to the front
        for(int i=k; i < n; i++) {
            nums[i-k] = nums[i];
        }
        
        // Copy back the k elemnents at the end
        for(int i=0; i < k; i++) {
            nums[n-k+i] = temp[i];
        }
    }
};

// Helper function to print the array
void printArray(vector<int> nums) {
    for(int val : nums) {
        cout << val << " ";
    }
    cout << endl;
}

int main() {
    vector nums = {1, 2, 3, 4, 5, 6};
    int k = 2;

    cout << "Initial array: ";
    printArray(nums);

    // Create an instance of the Solution class
    Solution sol;
    
    /* Function call to rotate the 
    array to the left by k places */
    sol.rotateArray(nums, k);
    
    cout << "Array after rotating elements by " << k << " places: ";
    printArray(nums);

    return 0;
}
import java.util.*;

class Solution {
    // Function to rotate the array to the left by k positions
    public void rotateArray(int[] nums, int k) {
        int n = nums.length; // Size of array
        k = k % n; // To avoid unnecessary rotations

        int[] temp = new int[k];

        // Store first k elements in a temporary array
        for (int i = 0; i < k; i++) {
            temp[i] = nums[i];
        }

        // Shift n-k elements of given array to the front
        for (int i = k; i < n; i++) {
            nums[i - k] = nums[i];
        }

        // Copy back the k elements at the end
        for (int i = 0; i < k; i++) {
            nums[n - k + i] = temp[i];
        }
    }
}

class Main {
    // Helper function to print the array
    public static void printArray(int[] nums) {
        for (int val : nums) {
            System.out.print(val + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4, 5, 6};
        int k = 2;

        System.out.println("Initial array: ");
        printArray(nums);

        // Create an instance of the Solution class
        Solution sol = new Solution();

        /* Function call to rotate the
        array to the left by k places */
        sol.rotateArray(nums, k);

        System.out.println("Array after rotating elements by " + k + " places: ");
        printArray(nums);
    }
}
class Solution:
    # Function to rotate the array to the left by k positions
    def rotateArray(self, nums, k):
        n = len(nums)  # Size of array
        k = k % n  # To avoid unnecessary rotations

        temp = []

        # Store first k elements in a temporary array
        for i in range(k):
            temp.append(nums[i])

        # Shift n-k elements of given array to the front
        for i in range(k, n):
            nums[i - k] = nums[i]

        # Copy back the k elements at the end
        for i in range(k):
            nums[n - k + i] = temp[i]


# Helper function to print the array
def printArray(nums):
    for val in nums:
        print(val, end=" ")
    print()


if __name__ == "__main__":
    nums = [1, 2, 3, 4, 5, 6]
    k = 2

    print("Initial array: ")
    printArray(nums)

    # Create an instance of the Solution class
    sol = Solution()

    # Function call to rotate the array to the left by k places
    sol.rotateArray(nums, k)

    print(f"Array after rotating elements by {k} places: ")
    printArray(nums)
class Solution {
    // Function to rotate the array to the left by k positions
    rotateArray(nums, k) {
        let n = nums.length; // Size of array
        k = k % n; // To avoid unnecessary rotations

        let temp = [];

        // Store first k elements in a temporary array
        for (let i = 0; i < k; i++) {
            temp.push(nums[i]);
        }

        // Shift n-k elements of given array to the front
        for (let i = k; i < n; i++) {
            nums[i - k] = nums[i];
        }

        // Copy back the k elements at the end
        for (let i = 0; i < k; i++) {
            nums[n - k + i] = temp[i];
        }
    }
}

// Helper function to print the array
function printArray(nums) {
    console.log(nums.join(' '));
}

const nums = [1, 2, 3, 4, 5, 6];
const k = 2;

console.log("Initial array: ");
printArray(nums);

// Create an instance of the Solution class
const sol = new Solution();

/* Function call to rotate the
array to the left by k places */
sol.rotateArray(nums, k);

console.log(`Array after rotating elements by ${k} places: `);
printArray(nums);

Complexity Analysis:

Time Complexity: O(N), where N is the length of the array. Three loops are used taking K, N-K, and K iterations respectively contributing to O(N+K). However, K can be N/2 in the worst case boiling down the time complexity as O(N). Space Complexity: O(k) due to the temporary list created to copy the K elements.