LCA in BT
Binary Trees
FAQs
Hard
Given a root of binary tree, find the lowest common ancestor (LCA) of two given nodes (p, q) in the tree.
The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).
Examples:
Input : root = [3, 5, 1, 6, 2, 0, 8, null, null, 7, 4] , p = 5, q = 1
Output : 3
Explanation :
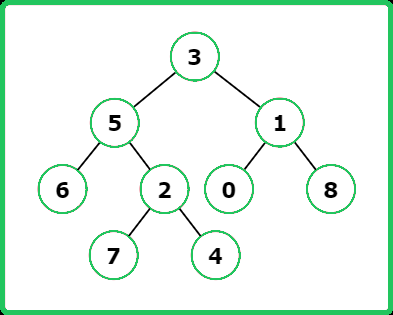
Input : root = [3, 5, 1, 6, 2, 0, 8, null, null, 7, 4] , p = 5, q = 4
Output : 5
Explanation :
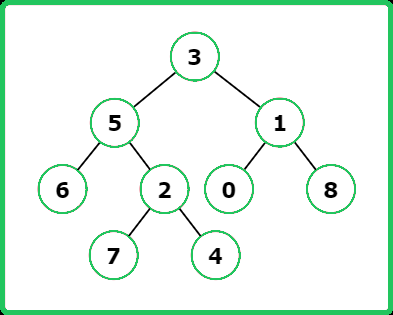
Input : root = [5, 1, 2, 8, 10, 4, 5, null, 6], p = 6, q = 10
Constraints
- 2 <= Number of Nodes <= 105
- -106 <= node.val <= 106
- All values in tree are unique.
Hints
- Recursively search the left subtree for p and q. Recursively search the right subtree for p and q.
- If both left and right subtrees return non-null values, then the current node is the LCA because p and q are in different subtrees. If only one subtree returns a non-null value, return that subtree’s value (it means both p and q are located in the same subtree). If both left and right return null, return null.
Company Tags
Rockstar Games
Robinhood
MongoDB
Micron Technology
American Express
Broadcom
Uber
Boston Consulting Group
Ernst & Young
Texas Instruments
Red Hat
Riot Games
Philips Healthcare
Lyft
Cloudflare
Epic Systems
Target
Zomato
Swiggy
Seagate Technology
Rakuten
Qualcomm
Mastercard
Snowflake
Unity Technologies
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
