N Queen

N Queen

Recursion FAQs (Hard) Hard

The N-Queens problem, while initially appearing as just a chess puzzle, actually has valuable implications in real-world applications
Its solution relies on a fundamental concept in technology: backtracking, which is used in recommendation algorithms, routing protocols, database queries optimizations and more
Any time you need to make a series of decisions, where each decision leads to a new set of choices, backtracking becomes a handy tool
The principles of this problem are even applied in branches of artificial intelligence for constraint satisfaction problems such as scheduling, map-coloring and Sudoku

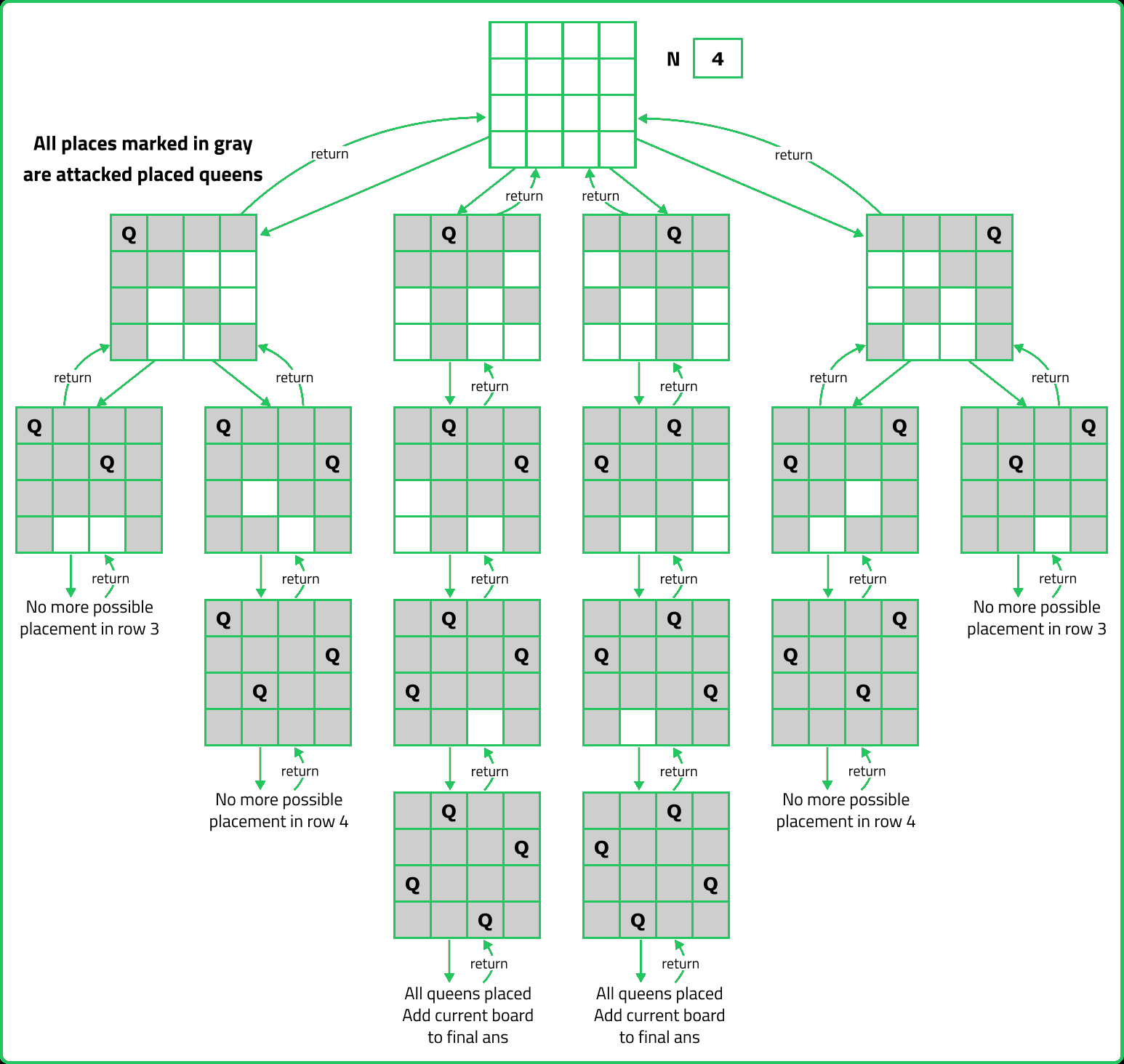
The challenge of arranging n queens on a n Ã n chessboard so that no two queens attack one another is known as the "n-queens puzzle."

Return every unique solution to the n-queens puzzle given an integer n. The answer can be returned in any sequence.

Every solution has a unique board arrangement for the placement of the n-queens, where 'Q' and '.' stand for a queen and an empty space, respectively.

Examples:

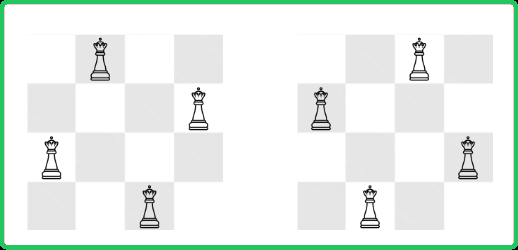
Input : n = 4

Output : [[".Q.." , "...Q" , "Q..." , "..Q."] , ["..Q." , "Q..." , "...Q" , ".Q.."]]

Explanation : There are two possible combinations as shown below.

Input : n = 2

Output : [ [] ]

Explanation : There is no possible combination for placing two queens on a board of size 2*2.

Input : n = 1

Constraints

1 <= n <= 9

Hints

Use backtracking to try placing queens row by row.
Use sets to efficiently track conflicts in columns, main diagonals, and anti-diagonals. Prune invalid branches early to reduce unnecessary computations.

Company Tags

Morgan Stanley Zoho Deloitte Robinhood Stripe Philips Healthcare Electronic Arts GE Healthcare Texas Instruments NVIDIA PwC Qualcomm Broadcom Mastercard Western Digital IBM Cloudflare JPMorgan Chase Lyft Roblox Bungie Snowflake Dropbox Seagate Technology HashiCorp Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Real-Life Solution

Imagine arranging a group of people in a hall where each person must have their own private space without being disturbed. Each person represents a queen and the hall represents the chessboard. The goal is to position each person such that no two people can see each other directly either in the same row, the same column, or along any diagonal. The task is to ensure that all individuals are placed in a way that respects these constraints, creating a harmonious arrangement.

Intuitive Recursion Process

The recursive process mimics placing each individual (queen) in a valid position (row) for a given column and then proceeding to place the next individual in the next column. Visualize this as a step-by-step arrangement where each step involves checking if a specific spot is free from conflicts. Start with an empty board and place the first queen in the first row of the first column. Move to the next column and try placing a queen in each row, one by one. If a spot is found where the queen can be placed without attacking others, move to the next column and repeat the process. If no safe spot is found in the current column, remove the last placed queen (backtrack) and try the next possible position for the previous queen. Continue this pattern of placing and removing queens until all columns have a queen or all possible configurations have been explored. This step-by-step placement ensures every possible arrangement is considered, and only valid solutions are kept.

Approach

Initialize an empty board of size n x n with all positions set to empty ('.').
Start with the first column (col = 0).
For the current column, try placing a queen in each row:
- Check if the current position (row, col) is safe by ensuring no queens are in the same row, column, or diagonal.
- If the position is safe, place a queen ('Q') at (row, col).
- Recursively attempt to place queens in the next column (col + 1).
- If placing the queen in the next column is successful, the solution is found.
- If no valid position is found for the next column, backtrack: remove the queen from (row, col) and try the next row in the current column.
If all columns are filled, add the current board configuration to the list of solutions.
Repeat the process until all possibilities are explored.
Return the list of all valid board configurations.

Dry Run

Solution

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Check if it's safe to place a queen at board[row][col]
    bool safe(vector<string>& board, int row, int col) {
        int r = row, c = col;

        // Check upper left diagonal
        while (r >= 0 && c >= 0) {
            if (board[r][c] == 'Q') return false;
            r--;
            c--;
        }

        // Reset to the original position
        r = row;
        c = col;

        // Check left side
        while (c >= 0) {
            if (board[r][c] == 'Q') return false;
            c--;
        }

        // Reset to the original position
        r = row;
        c = col;

        // Check lower left diagonal
        while (r < board.size() && c >= 0) {
            if (board[r][c] == 'Q') return false;
            r++;
            c--;
        }

        // If no queens are found, it's safe
        return true;
    }

    // Function to place queens on the board
    void func(int col, vector<vector<string>>& ans, vector<string>& board) {
        // If all columns are filled, add the solution to the answer
        if (col == board.size()) {
            ans.push_back(board);
            return;
        }

        // Try placing a queen in each row for the current column
        for (int row = 0; row < board.size(); row++) {
            // Check if it's safe to place a queen
            if (safe(board, row, col)) {
                // Place the queen
                board[row][col] = 'Q';

                // Recursively place queens in the next columns
                func(col + 1, ans, board);

                // Remove the queen and backtrack
                board[row][col] = '.';
            }
        }
    }

    // Solve the N-Queens problem
    vector<vector<string>> solveNQueens(int n) {
        // List to store the solutions
        vector<vector<string>> ans;
        // Initialize the board with empty cells
        vector<string> board(n, string(n, '.'));

        // Start placing queens from the first column
        func(0, ans, board);
        return ans;
    }
};

// Main method to test the solution
int main() {
    Solution solution;
    int n = 4; // Example with 4 queens
    vector<vector<string>> solutions = solution.solveNQueens(n);

    // Print all solutions
    for (const auto& sol : solutions) {
        for (const auto& row : sol) {
            cout << row << endl;
        }
        cout << endl;
    }

    return 0;
}
import java.util.ArrayList;
import java.util.List;

class Solution {

    // Check if it's safe to place a queen at board[row][col]
    public boolean safe(List<String> board, int row, int col) {
        int r = row, c = col;
        
        // Check upper left diagonal
        while (r >= 0 && c >= 0) {
            if (board.get(r).charAt(c) == 'Q') return false;
            r--;
            c--;
        }

        // Reset to the original position
        r = row;
        c = col;
        
        // Check left side
        while (c >= 0) {
            if (board.get(r).charAt(c) == 'Q') return false;
            c--;
        }

        // Reset to the original position
        r = row;
        c = col;
        
        // Check lower left diagonal
        while (r < board.size() && c >= 0) {
            if (board.get(r).charAt(c) == 'Q') return false;
            r++;
            c--;
        }

        // If no queens are found, it's safe
        return true;
    }

    // Function to place queens on the board
    public void func(int col, List<List<String>> ans, List<String> board) {
        // If all columns are filled, add the solution to the answer
        if (col == board.size()) {
            ans.add(new ArrayList<>(board));
            return;
        }

        // Try placing a queen in each row for the current column
        for (int row = 0; row < board.size(); row++) {
            // Check if it's safe to place a queen
            if (safe(board, row, col)) {
                // Place the queen
                char[] charArray = board.get(row).toCharArray();
                charArray[col] = 'Q';
                board.set(row, new String(charArray));
                
                // Recursively place queens in the next columns
                func(col + 1, ans, board);
                
                // Remove the queen and backtrack
                charArray[col] = '.';
                board.set(row, new String(charArray));
            }
        }
    }

    // Solve the N-Queens problem
    public List<List<String>> solveNQueens(int n) {
        // List to store the solutions
        List<List<String>> ans = new ArrayList<>();
        // Initialize the board with empty cells
        List<String> board = new ArrayList<>();
        String s = ".".repeat(n);
        for (int i = 0; i < n; i++) {
            board.add(s);
        }

        // Start placing queens from the first column
        func(0, ans, board);
        return ans;
    }

    // Main method to test the solution
    public static void main(String[] args) {
        Solution solution = new Solution();
        int n = 4; // Example with 4 queens
        List<List<String>> solutions = solution.solveNQueens(n);
        
        // Print all solutions
        for (List<String> sol : solutions) {
            for (String row : sol) {
                System.out.println(row);
            }
            System.out.println();
        }
    }
}
class Solution:
    # Check if it's safe to place a queen at board[row][col]
    def safe(self, board, row, col):
        r, c = row, col
        
        # Check upper left diagonal
        while r >= 0 and c >= 0:
            if board[r][c] == 'Q':
                return False
            r -= 1
            c -= 1

        # Reset to the original position
        r, c = row, col
        
        # Check left side
        while c >= 0:
            if board[r][c] == 'Q':
                return False
            c -= 1

        # Reset to the original position
        r, c = row, col
        
        # Check lower left diagonal
        while r < len(board) and c >= 0:
            if board[r][c] == 'Q':
                return False
            r += 1
            c -= 1

        # If no queens are found, it's safe
        return True

    # Function to place queens on the board
    def func(self, col, ans, board):
        # If all columns are filled, add the solution to the answer
        if col == len(board):
            ans.append(list(board))
            return

        # Try placing a queen in each row for the current column
        for row in range(len(board)):
            # Check if it's safe to place a queen
            if self.safe(board, row, col):
                # Place the queen
                board[row] = board[row][:col] + 'Q' + board[row][col+1:]
                
                # Recursively place queens in the next columns
                self.func(col + 1, ans, board)
                
                # Remove the queen and backtrack
                board[row] = board[row][:col] + '.' + board[row][col+1:]

    # Solve the N-Queens problem
    def solveNQueens(self, n):
        # List to store the solutions
        ans = []
        # Initialize the board with empty cells
        board = ["." * n for _ in range(n)]

        # Start placing queens from the first column
        self.func(0, ans, board)
        return ans

# Main method to test the solution
if __name__ == "__main__":
    solution = Solution()
    n = 4 # Example with 4 queens
    solutions = solution.solveNQueens(n)

    # Print all solutions
    for sol in solutions:
        for row in sol:
            print(row)
        print()
class Solution {
    // Check if it's safe to place a queen at board[row][col]
    safe(board, row, col) {
        let r = row, c = col;

        // Check upper left diagonal
        while (r >= 0 && c >= 0) {
            if (board[r][c] === 'Q') return false;
            r--;
            c--;
        }

        // Reset to the original position
        r = row;
        c = col;

        // Check left side
        while (c >= 0) {
            if (board[r][c] === 'Q') return false;
            c--;
        }

        // Reset to the original position
        r = row;
        c = col;

        // Check lower left diagonal
        while (r < board.length && c >= 0) {
            if (board[r][c] === 'Q') return false;
            r++;
            c--;
        }

        // If no queens are found, it's safe
        return true;
    }

    // Function to place queens on the board
    func(col, ans, board) {
        // If all columns are filled, add the solution to the answer
        if (col === board.length) {
            ans.push([...board]);
            return;
        }

        // Try placing a queen in each row for the current column
        for (let row = 0; row < board.length; row++) {
            // Check if it's safe to place a queen
            if (this.safe(board, row, col)) {
                // Place the queen
                let charArray = board[row].split('');
                charArray[col] = 'Q';
                board[row] = charArray.join('');
                
                // Recursively place queens in the next columns
                this.func(col + 1, ans, board);
                
                // Remove the queen and backtrack
                charArray[col] = '.';
                board[row] = charArray.join('');
            }
        }
    }

    // Solve the N-Queens problem
    solveNQueens(n) {
        // List to store the solutions
        const ans = [];
        // Initialize the board with empty cells
        const board = Array(n).fill('.'.repeat(n));

        // Start placing queens from the first column
        this.func(0, ans, board);
        return ans;
    }
}

// Main method to test the solution
const solution = new Solution();
const n = 4; // Example with 4 queens
const solutions = solution.solveNQueens(n);

// Print all solutions
for (const sol of solutions) {
    for (const row of sol) {
        console.log(row);
    }
    console.log();
}

Complexity Analysis

Time Complexity : The time complexity is O(N!), where N is the number of queens, due to the recursive search through potential placements and backtracking.

Space Complexity : The space complexity is O(N), for the recursion stack and the storage of the solutions.

Code

Problem List