Subsets II

Subsets II

Recursion FAQs (Medium) Medium

Given an integer array nums, which can have duplicate entries, provide the power set. Duplicate subsets cannot exist in the solution set. Return the answer in any sequence.

Examples:

Input : nums = [1, 2, 2]

Output : [ [ ] , [1] , [1, 2] , [1, 2, 2] , [2] , [2, 2] ]

Input : nums = [1, 2]

Output : [ [ ], [1] , [2] , [1, 2] ]

Input : nums = [1, 3, 3]

Constraints

1 <= nums.length <= 10
-10 <= nums[i] <= 10

Hints

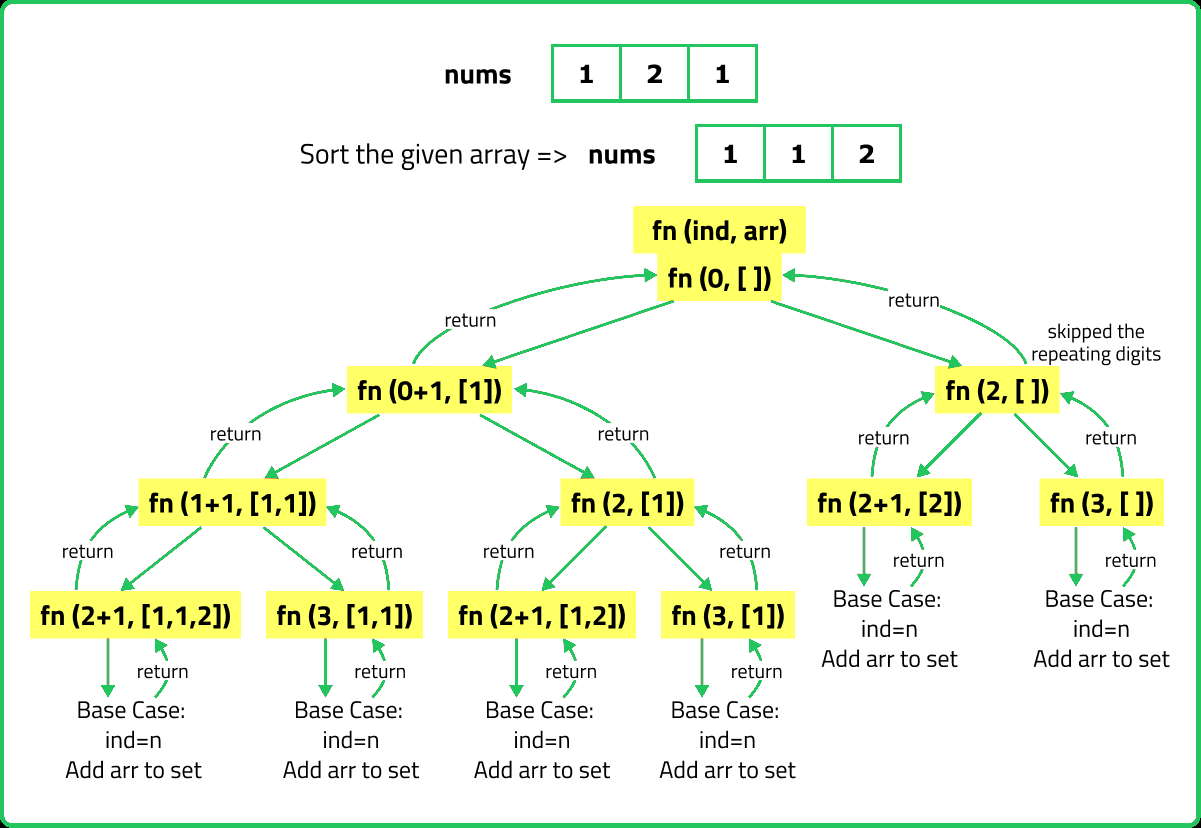
Sort the input array nums to group duplicate elements together. While generating subsets, skip duplicate elements to avoid generating the same subset multiple times
Start with an empty subset. For each element in nums, add it to all existing subsets. To handle duplicates, only extend subsets created in the previous iteration for duplicate elements.

Company Tags

Goldman Sachs OYO Rooms Optum Chewy Zomato Etsy Salesforce Rockstar Games Flipkart Stripe Electronic Arts Uber Deloitte Rakuten Freshworks Zoho Intel Oracle Bungie Walmart Roblox Zynga HCL Technologies AMD Databricks Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

              document.body.innerHTML = '';
              const iframeHTML = `
                <div style="padding-top:56.25%;position:relative;">
                  <iframe 
                    src="https://app.tpstreams.com/embed/atsjxr/9uuJ8yZBBas/?access_token=33e345b1-9f22-4382-8c5c-7e49a75d8027" 
                    style="border:0;max-width:100%;position:absolute;top:0;left:0;height:100%;width:100%;" 
                    allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" 
                    allowfullscreen="" 
                    frameborder="0">
                  </iframe>
                </div>
              `;
              document.body.innerHTML = iframeHTML;
              
              const script = document.createElement('script');
              script.src = 'https://static.testpress.in/static/js/player.js';
              document.head.appendChild(script);
              
              script.onload = () => {
                const iframe = document.querySelector('iframe');
                const player = new Testpress.Player(iframe);
              
                player.loaded().then(() => {
                  console.log('Player is ready now');
                });
              
                player.on('play', () => {
                  console.log('Played the video');
                });
              };

Intuition

Imagine a task to create all possible groups of items from a list that might have repeated items, ensuring no group is duplicated. The goal is to include each item or skip it, but if an item is skipped, all identical items must also be skipped to avoid duplicate groups. This mirrors the recursive process by methodically including or excluding each item while traversing the list. If an item is included, the process continues with the next item. If an item is excluded, the process skips all its duplicates to maintain unique groups. This step-by-step approach ensures all potential combinations are explored while preventing duplicates.

Approach

Sort the input list to group identical items together, simplifying the process of skipping duplicates.
Use a helper function to explore subsets recursively, starting from the first item and tracking the current subset.
For each item, choose to include it in the current subset and recurse to the next item. Then, backtrack and exclude the item, skipping any subsequent duplicates, and recurse again.
Upon reaching the end of the list, add the current subset to the result list. This ensures all possible subsets are captured while avoiding duplicates.

Dry Run

Solution

#include<bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Helper function to generate subsets
    void func(int ind, vector<int> &arr, vector<int> &nums, vector<vector<int>> &ans) {
        // Base case: if index reaches the end of nums
        if(ind == nums.size()) {
            // Add the current subset (arr) to the result
            ans.push_back(arr);
            return;
        }
        
        // Include the current element in the subset
        arr.push_back(nums[ind]);
        // Recur for the next index
        func(ind+1, arr, nums, ans);
        // Backtrack: remove the current element from the subset
        arr.pop_back();

        // Skip duplicates and recur for the next unique element
        for(int j = ind + 1; j < nums.size(); j++) {
            if(nums[j] != nums[ind]) {
                func(j, arr, nums, ans);
                return;
            }
        }

        // Ensure the function finishes when no more unique elements are left
        func(nums.size(), arr, nums, ans);
    }

public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<vector<int>> ans;  // Resulting list of subsets
        vector<int> arr;          // Current subset
        sort(nums.begin(), nums.end()); // Sort the array to handle duplicates
        func(0, arr, nums, ans);  // Start recursion
        return ans; 
    }
};

int main() {
    Solution sol;
    vector<int> nums = {1, 2, 2};  // Example input
    vector<vector<int>> result = sol.subsetsWithDup(nums);

    // Print the resulting subsets
    for(const auto& subset : result) {
        cout << "[ ";
        for(int num : subset) {
            cout << num << " ";
        }
        cout << "]\n";
    }

    return 0;
}
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

class Solution {
    private void func(int ind, List<Integer> arr, int[] nums, List<List<Integer>> ans) {
        // If index reaches the end of nums
        if (ind == nums.length) {
            // Add the current subset (arr) to the result
            ans.add(new ArrayList<>(arr));
            return;
        }
        
        // Include the current element in the subset
        arr.add(nums[ind]);
        // Recur for the next index
        func(ind + 1, arr, nums, ans);
        // Backtrack: remove the current element from the subset
        arr.remove(arr.size() - 1);
        
        // Skip duplicates and recur for the next unique element
        for (int j = ind + 1; j < nums.length; j++) {
            if (nums[j] != nums[ind]) {
                func(j, arr, nums, ans);
                return;
            }
        }
        
        // Ensure the function finishes when no more unique elements are left
        func(nums.length, arr, nums, ans);
    }

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();  // Resulting list of subsets
        List<Integer> arr = new ArrayList<>();        // Current subset
        Arrays.sort(nums);  // Sort the array to handle duplicates
        func(0, arr, nums, ans);  // Start recursion
        return ans;
    }

    public static void main(String[] args) {
        Solution sol = new Solution();
        int[] nums = {1, 2, 2};  // Example input
        List<List<Integer>> result = sol.subsetsWithDup(nums);
        
        // Print the resulting subsets
        for (List<Integer> subset : result) {
            System.out.println(subset);
        }
    }
}
class Solution:
    def func(self, ind, arr, nums, ans):
        # If index reaches the end of nums
        if ind == len(nums):
            # Add the current subset (arr) to the result
            ans.append(arr.copy())
            return
        
        # Include the current element in the subset
        arr.append(nums[ind])
        # Recur for the next index
        self.func(ind + 1, arr, nums, ans)
        # Backtrack: remove the current element from the subset
        arr.pop()
        
        # Skip duplicates and recur for the next unique element
        for j in range(ind + 1, len(nums)):
            if nums[j] != nums[ind]:
                self.func(j, arr, nums, ans)
                return
        
        # Ensure the function finishes when no more unique elements are left
        self.func(len(nums), arr, nums, ans)
    
    def subsetsWithDup(self, nums):
        ans = []  # Resulting list of subsets
        arr = []  # Current subset
        nums.sort()  # Sort the array to handle duplicates
        self.func(0, arr, nums, ans)  # Start recursion
        return ans

if __name__ == "__main__":
    sol = Solution()
    nums = [1, 2, 2]  # Example input
    result = sol.subsetsWithDup(nums)
    
    # Print the resulting subsets
    for subset in result:
        print(subset)
class Solution {
    func(ind, arr, nums, ans) {
        // If index reaches the end of nums
        if (ind === nums.length) {
            // Add the current subset (arr) to the result
            ans.push([...arr]);
            return;
        }
        
        // Include the current element in the subset
        arr.push(nums[ind]);
        // Recur for the next index
        this.func(ind + 1, arr, nums, ans);
        // Backtrack: remove the current element from the subset
        arr.pop();
        
        // Skip duplicates and recur for the next unique element
        for (let j = ind + 1; j < nums.length; j++) {
            if (nums[j] !== nums[ind]) {
                this.func(j, arr, nums, ans);
                return;
            }
        }
        
        // Ensure the function finishes when no more unique elements are left
        this.func(nums.length, arr, nums, ans);
    }

    subsetsWithDup(nums) {
        const ans = [];  // Resulting list of subsets
        const arr = [];  // Current subset
        nums.sort((a, b) => a - b);  // Sort the array to handle duplicates
        this.func(0, arr, nums, ans);  // Start recursion
        return ans;
    }
}

const sol = new Solution();
const nums = [1, 2, 2];  // Example input
const result = sol.subsetsWithDup(nums);

// Print the resulting subsets
for (const subset of result) {
    console.log(subset);
}

Complexity Analysis

Time Complexity: O(2^N * N) - Each element is either included or excluded, leading to an exponential number of subsets.

Space Complexity: O(N) - The space complexity is dominated by the recursion stack, which can go as deep as the number of elements in the input list.

Code

Problem List