Longest common subsequence
Dynamic Programming
DP on strings
Hard
- This problem, often known as the Longest Common Subsequence (LCS) problem, underlies the logic of many diff utilities and version control systems like Git
- The diff tools use this problem to compare different versions of code or text files, and find the minimum number of changes needed to transform one version to another
- This allows developers to efficiently track and manage changes in their projects over time
Given two strings str1 and str2, find the length of their longest common subsequence.
A subsequence is a sequence that appears in the same relative order but not necessarily contiguous and a common subsequence of two strings is a subsequence that is common to both strings.
Examples:
Input: str1 = "bdefg", str2 = "bfg"
Output: 3
Explanation: The longest common subsequence is "bfg", which has a length of 3.
Input: str1 = "mnop", str2 = "mnq"
Output: 2
Explanation: The longest common subsequence is "mn", which has a length of 2.
Input: str1 = "abc", str2 = "dafb"
Constraints
- n=str1.length
- m=str2.length
- 1<= n, m <=103
- str1 and str2 are in lowercase alphabet
Hints
- Define dp[i][j] as the length of the LCS of the first i characters of str1 and the first j characters of str2.
- If str1[i-1] == str2[j-1], the LCS extends dp[i][j]=1+dp[i−1][j−1]. Otherwise, we take the maximum LCS found by excluding either character dp[i][j]=max(dp[i−1][j],dp[i][j−1])
Company Tags
Goldman Sachs
OYO Rooms
Swiggy
IBM
Byju's
Databricks
Instacart
Bain & Company
Dropbox
Walmart
Broadcom
Zomato
KPMG
Square
Rakuten
Pinterest
Zynga
Nutanix
Bungie
JPMorgan Chase
Etsy
Epic Systems
PwC
GE Healthcare
McKinsey & Company
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
We are given two strings, S1, and S2 (suppose of same length n), the simplest approach will be to generate all the subsequences and store them, then manually find out the longest common subsequence.
We would want to try something that can give us the longest common subsequence on the way of generating all subsequences. To generate all subsequences we will use recursion and in the recursive logic we will figure out a way to solve this problem.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given two strings S1 and S2. A single variable can’t express both the strings at the same time, so we will use two variables 'ind1' and 'ind2'. They mean that we are considering string S1 from index 0 to 'ind1' and string S2 from index 0 to 'ind2'. So f(ind1, ind2) will give the longest common subsequence in S1 and S2.
- Explore all possibilities at a given index: In the function f(ind1,ind2), ind1 and ind2 are representing two characters from strings S1 and S2 respectively. For example:
Now, there can be two possibilities,
If (S1[ind1] == S2[ind2]) as in the figure below. In this case this common element will represent a unit length common subsequence, so we can say that we have found one character and we can shrink both the strings by 1 to find the longest common subsequence in the remaining pair of strings.
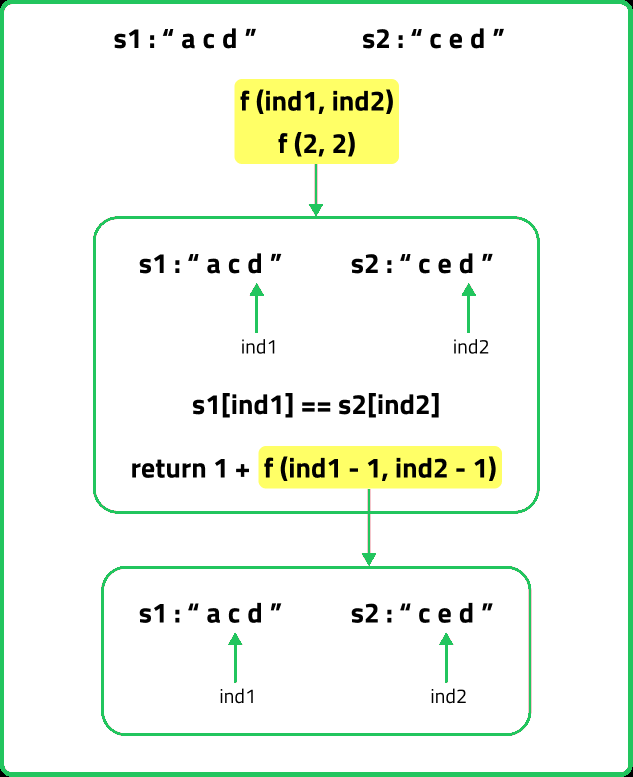
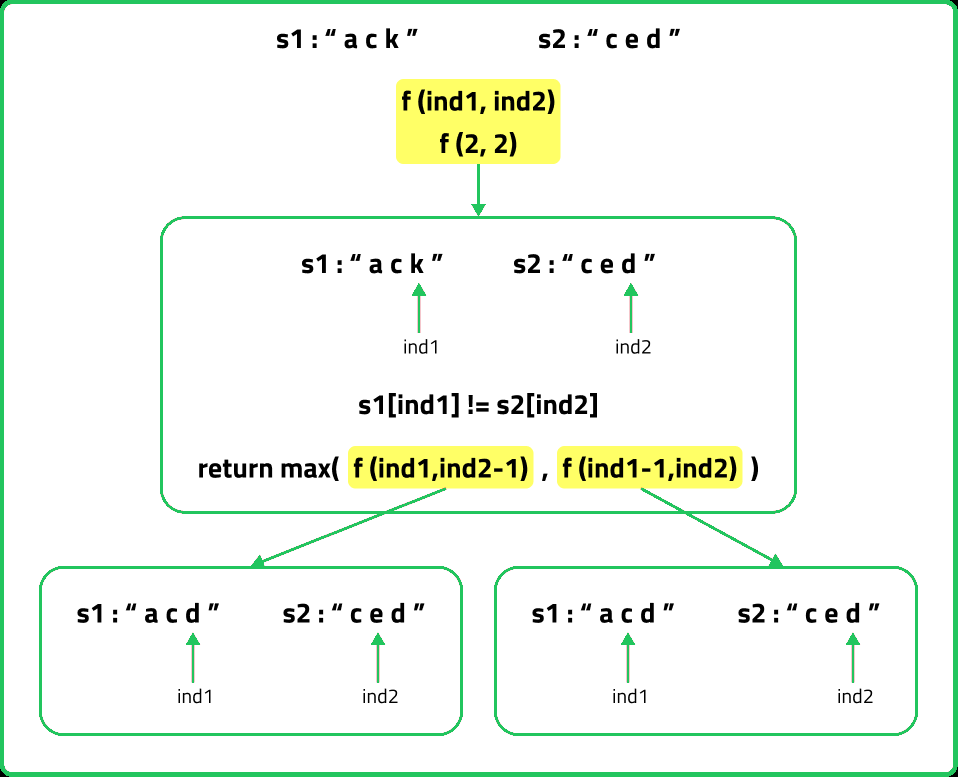
If (S1[ind1] != S2[ind2]) as in the figure given below. In this case we know that the current characters represented by ind1 and ind 2 will be different. So, we need to compare the ind1 character with shrunk S2 and ind2 with shrunk S1. But how do we make this comparison ? If we make a single recursive call as we did above to f(ind1-1,ind2-1), we may lose some characters of the subsequence. Therefore we make two recursive calls: one to f(ind1,ind2-1) (shrinking only S1) and one to f(ind1-1,ind2) (shrinking only S2). Then when we return max of both the calls.
123456789/*It is pseudocode and it is not tied to any specific programming language.*/ f(ind1, ind2){ if(s1[ind1] == s2[ind2] return 1 + f(ind1 - 1, ind2 - 2) else return 0 + max(f(ind1, ind2-1), f(ind1 - 1, ind2)) }
- Return the maximum of the choices: In the first case, we have only one choice but in the second case we have two choices, as we have to return the longest common subsequences, we will return the maximum of both the choices in the second case.
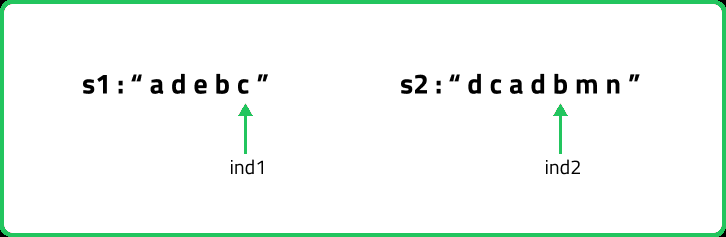
- Base Case: For a case like this:
As S1[ind1] != S2[ind2], we will make a call to f(0-1,1), i.e f(-1,1) but a negative index simply means that there are no more indexes to be explored, so we simply return 0. Same is the case when S1[ind1]==S2[ind2]. So, when any of the index (ind1, ind2) becomes negative we will return 0.
1234567891011121314151617181920212223242526272829303132333435363738394041424344
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
int func(string& s1, string& s2, int ind1, int ind2) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the characters at the current
indices match, increment the LCS length*/
if (s1[ind1] == s2[ind2])
return 1 + func(s1, s2, ind1 - 1, ind2 - 1);
else
return max(func(s1, s2, ind1, ind2 - 1), func(s1, s2, ind1 - 1, ind2));
}
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
//Return the result
return func(str1, str2, n - 1, m - 1);
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940
import java.util.*;
class Solution {
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
private int func(String s1, String s2, int ind1, int ind2) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the characters at the current
indices match, increment the LCS length*/
if (s1.charAt(ind1) == s2.charAt(ind2))
return 1 + func(s1, s2, ind1 - 1, ind2 - 1);
else
return Math.max(func(s1, s2, ind1, ind2 - 1), func(s1, s2, ind1 - 1, ind2));
}
/* Function to calculate the length
of the Longest Common Subsequence*/
public int lcs(String str1, String str2) {
int n = str1.length();
int m = str2.length();
// Return the result
return func(str1, str2, n - 1, m - 1);
}
public static void main(String[] args) {
String s1 = "acd";
String s2 = "ced";
// Create an instance of Solution class
Solution sol = new Solution();
// Call the function to find and output
System.out.println("The Length of Longest Common Subsequence is " + sol.lcs(s1, s2));
}
}
12345678910111213141516171819202122232425262728293031323334
class Solution:
""" Function to find the length of the
Longest Common Subsequence (LCS)"""
def func(self, s1, s2, ind1, ind2):
# Base case
if ind1 < 0 or ind2 < 0:
return 0
""" If the characters at the current
indices match, increment the LCS length"""
if s1[ind1] == s2[ind2]:
return 1 + self.func(s1, s2, ind1 - 1, ind2 - 1)
else:
return max(self.func(s1, s2, ind1, ind2 - 1), self.func(s1, s2, ind1 - 1, ind2))
""" Function to calculate the length
of the Longest Common Subsequence"""
def lcs(self, str1, str2):
n = len(str1)
m = len(str2)
# Return the result
return self.func(str1, str2, n - 1, m - 1)
if __name__ == "__main__":
s1 = "acd"
s2 = "ced"
# Create an instance of Solution class
sol = Solution()
# Call the function to find and output
print("The Length of Longest Common Subsequence is", sol.lcs(s1, s2))
123456789101112131415161718192021222324252627282930313233343536
class Solution {
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
func(s1, s2, ind1, ind2) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the characters at the current
indices match, increment the LCS length*/
if (s1[ind1] === s2[ind2])
return 1 + this.func(s1, s2, ind1 - 1, ind2 - 1);
else
return Math.max(this.func(s1, s2, ind1, ind2 - 1), this.func(s1, s2, ind1 - 1, ind2));
}
/* Function to calculate the length
of the Longest Common Subsequence*/
lcs(str1, str2) {
const n = str1.length;
const m = str2.length;
// Return the result
return this.func(str1, str2, n - 1, m - 1);
}
}
const s1 = "acd";
const s2 = "ced";
// Create an instance of Solution class
const sol = new Solution();
// Call the function to find and output
console.log("The Length of Longest Common Subsequence is", sol.lcs(s1, s2));
Complexity Analysis:
Time Complexity: O(2N+M), Where N is the length of the given string.Space Complexity:O(N+M), As we are using a recursion stack space(O(N+M)).
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
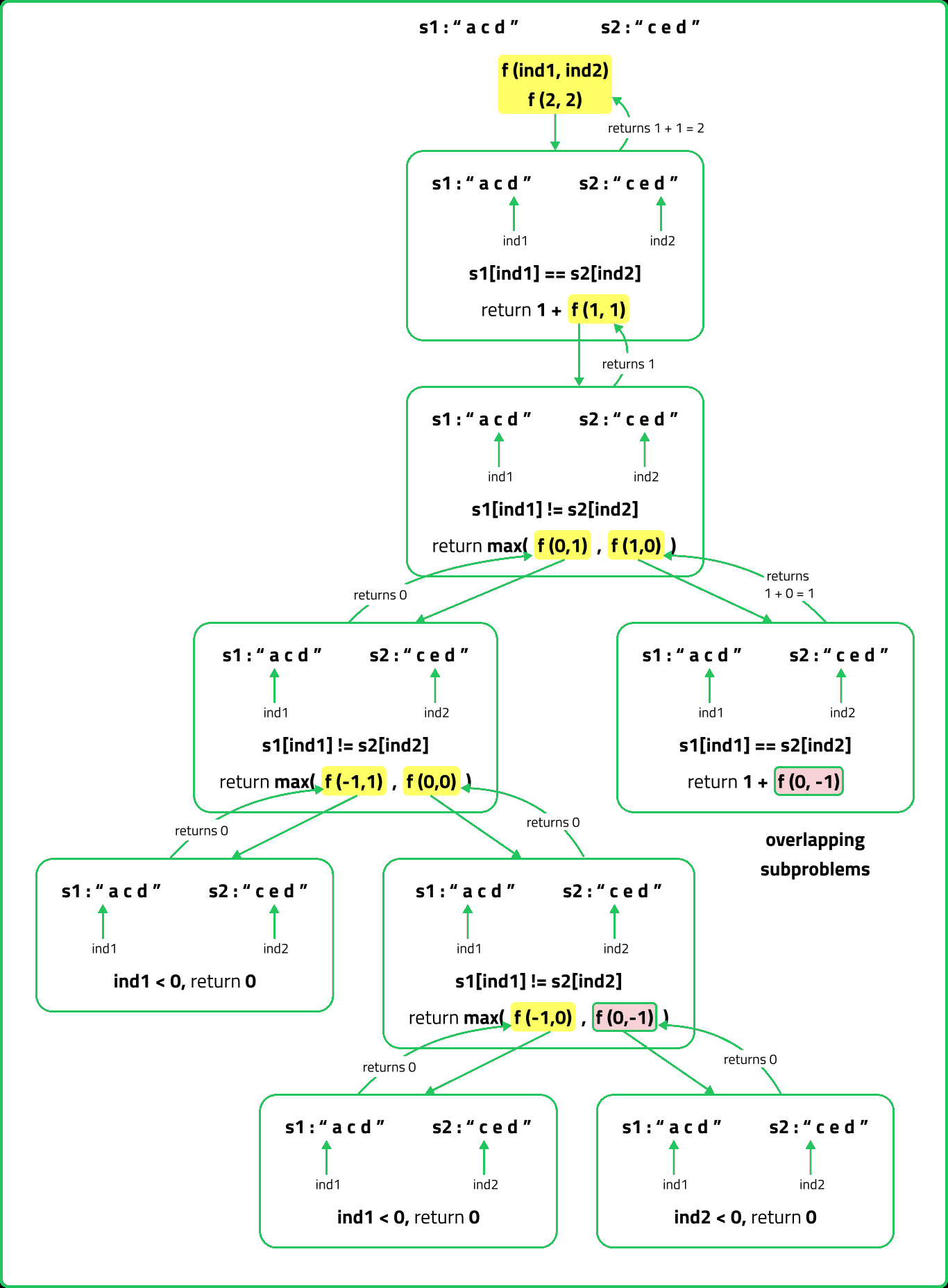
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][m]: where n and m are the lengths of S1 and S2 respectively. As there are two changing parameters in the recursive solution, 'ind1' and 'ind2'. The maximum value 'ind1' can attain is (n) and 'ind2' can attain maximum value of (m). Therefore, we need 2D dp array.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
The dp array shows the calculations of the subproblems, initialize it with -1 to show that no subproblem is solved yet.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
int func(string& s1, string& s2, int ind1, int ind2, vector<vector<int>>& dp) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the result for this pair of indices
is already calculated, return it*/
if (dp[ind1][ind2] != -1)
return dp[ind1][ind2];
/* If the characters at the current
indices match, increment the LCS length*/
if (s1[ind1] == s2[ind2])
return dp[ind1][ind2] = 1 + func(s1, s2, ind1 - 1, ind2 - 1, dp);
else
return dp[ind1][ind2] = max(func(s1, s2, ind1, ind2 - 1, dp), func(s1, s2, ind1 - 1, ind2, dp));
}
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
vector<vector<int>> dp(n, vector<int>(m, -1));
//Return the result
return func(str1, str2, n - 1, m - 1, dp);
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
import java.util.*;
class Solution {
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
private int func(String s1, String s2, int ind1, int ind2, int[][] dp) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the result for this pair of indices
is already calculated, return it*/
if (dp[ind1][ind2] != -1)
return dp[ind1][ind2];
/* If the characters at the current
indices match, increment the LCS length*/
if (s1.charAt(ind1) == s2.charAt(ind2))
return dp[ind1][ind2] = 1 + func(s1, s2, ind1 - 1, ind2 - 1, dp);
else
return dp[ind1][ind2] = Math.max(func(s1, s2, ind1, ind2 - 1, dp), func(s1, s2, ind1 - 1, ind2, dp));
}
/* Function to calculate the length
of the Longest Common Subsequence*/
public int lcs(String str1, String str2) {
int n = str1.length();
int m = str2.length();
int[][] dp = new int[n][m];
for (int[] row : dp)
Arrays.fill(row, -1);
//Return the result
return func(str1, str2, n - 1, m - 1, dp);
}
public static void main(String[] args) {
String s1 = "acd";
String s2 = "ced";
//Create an instance of Solution class
Solution sol = new Solution();
// Call the function to find and output
System.out.println("The Length of Longest Common Subsequence is " + sol.lcs(s1, s2));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041
class Solution:
""" Function to find the length of the
Longest Common Subsequence (LCS)"""
def func(self, s1, s2, ind1, ind2, dp):
# Base case
if ind1 < 0 or ind2 < 0:
return 0
""" If the result for this pair of indices
is already calculated, return it"""
if dp[ind1][ind2] != -1:
return dp[ind1][ind2]
""" If the characters at the current
indices match, increment the LCS length"""
if s1[ind1] == s2[ind2]:
dp[ind1][ind2] = 1 + self.func(s1, s2, ind1 - 1, ind2 - 1, dp)
else:
dp[ind1][ind2] = max(self.func(s1, s2, ind1, ind2 - 1, dp), self.func(s1, s2, ind1 - 1, ind2, dp))
return dp[ind1][ind2]
""" Function to calculate the length
of the Longest Common Subsequence"""
def lcs(self, str1, str2):
n = len(str1)
m = len(str2)
dp = [[-1] * m for _ in range(n)]
# Return the result
return self.func(str1, str2, n - 1, m - 1, dp)
if __name__ == "__main__":
s1 = "acd"
s2 = "ced"
# Create an instance of Solution class
sol = Solution()
# Call the function to find and output
print("The Length of Longest Common Subsequence is", sol.lcs(s1, s2))
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
class Solution {
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
func(s1, s2, ind1, ind2, dp) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the result for this pair of indices
is already calculated, return it*/
if (dp[ind1][ind2] !== -1)
return dp[ind1][ind2];
/* If the characters at the current
indices match, increment the LCS length*/
if (s1[ind1] === s2[ind2]){
dp[ind1][ind2] = 1 + this.func(s1, s2, ind1 - 1, ind2 - 1, dp);
return dp[ind1][ind2];
}
else{
dp[ind1][ind2] = Math.max(this.func(s1, s2, ind1, ind2 - 1, dp), this.func(s1, s2, ind1 - 1, ind2, dp));
return dp[ind1][ind2];
}
}
/* Function to calculate the length
of the Longest Common Subsequence*/
lcs(str1, str2) {
const n = str1.length;
const m = str2.length;
const dp = Array.from({ length: n }, () => Array(m).fill(-1));
// Return the result
return this.func(str1, str2, n - 1, m - 1, dp);
}
}
const s1 = "acd";
const s2 = "ced";
// Create an instance of Solution class
const sol = new Solution();
// Call the function to find and output
console.log("The Length of Longest Common Subsequence is", sol.lcs(s1, s2));
Complexity Analysis:
Time Complexity: O(N*M), N is the length of string S1 and M is the length of string S2. There are N*M states therefore at max ‘N*M’ new problems will be solved.Space Complexity:O(N*M) + O(N+M), We are using an auxiliary recursion stack space(O(N+M)) and a 2D array (O(N*M)).
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n][m]: where n and m are the lengths of S1 and S2 respectively. As there are two changing parameters in the recursive solution, 'ind1' and 'ind2'. The maximum value 'ind1' can attain is (n) and 'ind2' can attain maximum value of (m). Therefore, we need 2D dp array.
- Setting Base Cases in the Array: In the recursive code, our base condition was when ind1 < 0 or ind2 < 0, but we can’t set the dp array’s index to -1. Therefore a hack for this issue is to shift every index by 1 towards the right.
- Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations. Keeping in mind the shifting of indexes, as for example S1[ind1] will be converted to S1[ind1-1].
- Returning the answer: At last dp[n][m] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.
Therefore, now the base case will be if(ind1==0 || ind2==0), return 0. So we will set dp array with 0 for ind1 = 0 and ind2 = 0.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, -1));
// Initialize the base cases
for (int i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (int i = 0; i <= m; i++) {
dp[0][i] = 0;
}
// Fill in the DP table to calculate the length of LCS
for (int ind1 = 1; ind1 <= n; ind1++) {
for (int ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1[ind1 - 1] == str2[ind2 - 1])
dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1];
/* Characters don't match, consider
the maximum from left or above*/
else
dp[ind1][ind2] = max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]);
}
}
// Return the length of Longest Common Subsequence
return dp[n][m];
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
import java.util.*;
class Solution {
/* Function to calculate the length
of the Longest Common Subsequence*/
public int lcs(String str1, String str2) {
int n = str1.length();
int m = str2.length();
int[][] dp = new int[n + 1][m + 1];
// Initialize the base cases
for (int i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (int i = 0; i <= m; i++) {
dp[0][i] = 0;
}
// Fill in the DP table to calculate length of LCS
for (int ind1 = 1; ind1 <= n; ind1++) {
for (int ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1.charAt(ind1 - 1) == str2.charAt(ind2 - 1))
dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1];
/* Characters don't match, consider
the maximum from left or above*/
else
dp[ind1][ind2] = Math.max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]);
}
}
// Return the length of Longest Common Subsequence
return dp[n][m];
}
public static void main(String[] args) {
String s1 = "acd";
String s2 = "ced";
// Create an instance of Solution class
Solution sol = new Solution();
// Call the function to find and output
System.out.println("The Length of Longest Common Subsequence is " + sol.lcs(s1, s2));
}
}
123456789101112131415161718192021222324252627282930313233343536373839
class Solution:
""" Function to calculate the length
of the Longest Common Subsequence"""
def lcs(self, str1, str2):
n = len(str1)
m = len(str2)
dp = [[0] * (m + 1) for _ in range(n + 1)]
# Initialize the base cases
for i in range(n + 1):
dp[i][0] = 0
for i in range(m + 1):
dp[0][i] = 0
# Fill in the DP table to calculate length of LCS
for ind1 in range(1, n + 1):
for ind2 in range(1, m + 1):
# Characters match, increment LCS length
if str1[ind1 - 1] == str2[ind2 - 1]:
dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1]
else:
dp[ind1][ind2] = max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1])
# Return the length of Longest Common Subsequence
return dp[n][m]
if __name__ == "__main__":
s1 = "acd"
s2 = "ced"
# Create an instance of Solution class
sol = Solution()
# Call the function to find and output
print("The Length of Longest Common Subsequence is", sol.lcs(s1, s2))
1234567891011121314151617181920212223242526272829303132333435363738394041424344
class Solution {
/* Function to calculate the length
of the Longest Common Subsequence */
lcs(str1, str2) {
const n = str1.length;
const m = str2.length;
const dp = Array.from({ length: n + 1 }, () => Array(m + 1).fill(0));
// Initialize the base cases
for (let i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (let i = 0; i <= m; i++) {
dp[0][i] = 0;
}
// Fill in the DP table to calculate length of LCS
for (let ind1 = 1; ind1 <= n; ind1++) {
for (let ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1[ind1 - 1] === str2[ind2 - 1])
dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1];
/* Characters don't match, consider
the maximum from left or above*/
else
dp[ind1][ind2] = Math.max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]);
}
}
// Return the length of Longest Common Subsequence
return dp[n][m];
}
}
const s1 = "acd";
const s2 = "ced";
// Create an instance of Solution class
const sol = new Solution();
// Call the function to find and output
console.log("The Length of Longest Common Subsequence is", sol.lcs(s1, s2));
Complexity Analysis:
Time Complexity: O(N*M), N is the length of string S1 and M is the length of string S2. There are two nested loops which are running for N*M.Space Complexity:O(N*M), As a 2D array of size N*M is used.
If we observe the relation obtained in tabulation approach, dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]. We are using just two rows: dp[ind1-1][ ], dp[ind][ ] in order to calculate any row.
So we are not required to contain an entire array, we can simply have two rows 'prev' and 'cur' where prev corresponds to dp[ind-1] and cur to dp[ind].
After declaring 'prev' and 'cur', replace dp[ind-1] to prev and dp[ind] with cur in the tabulation code. Following the same logic of tabulation, we will calculate cur[ind] in each iteration and after the inner loop executes, we will set prev = cur, so that the cur row can serve as prev for the next index.
After end of the execution, return prev[m] as our answer, as it will hold the cumulative result of the overall calculation.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
/* Initialize two vectors to store the
current and previous rows of the DP table*/
vector<int> prev(m + 1, 0), cur(m + 1, 0);
/* Base case is covered as we have initialized
the prev and cur vectors to 0.*/
for (int ind1 = 1; ind1 <= n; ind1++) {
for (int ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1[ind1 - 1] == str2[ind2 - 1])
cur[ind2] = 1 + prev[ind2 - 1];
else
cur[ind2] = max(prev[ind2], cur[ind2 - 1]);
}
// Update the previous row with current row
prev = cur;
}
// Return the length of Longest Common Subsequence
return prev[m];
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445
import java.util.*;
class Solution {
/* Function to calculate the length
of the Longest Common Subsequence */
public int lcs(String str1, String str2) {
int n = str1.length();
int m = str2.length();
/* Initialize two arrays to store the
current and previous rows of the DP table */
int[] prev = new int[m + 1];
int[] cur = new int[m + 1];
/* Base case is covered as we have initialized
the prev and cur arrays to 0. */
for (int ind1 = 1; ind1 <= n; ind1++) {
for (int ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1.charAt(ind1 - 1) == str2.charAt(ind2 - 1))
cur[ind2] = 1 + prev[ind2 - 1];
else
cur[ind2] = Math.max(prev[ind2], cur[ind2 - 1]);
}
// Update the previous row with the current row
System.arraycopy(cur, 0, prev, 0, m + 1);
}
// Return the length of Longest Common Subsequence
return prev[m];
}
public static void main(String[] args) {
String s1 = "acd";
String s2 = "ced";
// Create an instance of Solution class
Solution sol = new Solution();
// Call the function to find and output
System.out.println("The Length of Longest Common Subsequence is " + sol.lcs(s1, s2));
}
}
123456789101112131415161718192021222324252627282930313233343536373839
class Solution:
""" Function to calculate the length
of the Longest Common Subsequence"""
def lcs(self, str1, str2):
n = len(str1)
m = len(str2)
""" Initialize two lists to store the
current and previous rows of the DP table"""
prev = [0] * (m + 1)
cur = [0] * (m + 1)
""" Base case is covered as we have initialized
the prev and cur lists to 0."""
for ind1 in range(1, n + 1):
for ind2 in range(1, m + 1):
# Characters match, increment LCS length
if str1[ind1 - 1] == str2[ind2 - 1]:
cur[ind2] = 1 + prev[ind2 - 1]
else:
cur[ind2] = max(prev[ind2], cur[ind2 - 1])
# Update the previous row with the current row
prev = cur[:]
# Return the length of Longest Common Subsequence
return prev[m]
if __name__ == "__main__":
s1 = "acd"
s2 = "ced"
# Create an instance of Solution class
sol = Solution()
# Call the function to find and output
print("The Length of Longest Common Subsequence is", sol.lcs(s1, s2))
12345678910111213141516171819202122232425262728293031323334353637383940414243
class Solution {
/* Function to calculate the length
of the Longest Common Subsequence */
lcs(str1, str2) {
const n = str1.length;
const m = str2.length;
/* Initialize two arrays to store the
current and previous rows of the DP table*/
const prev = new Array(m + 1).fill(0);
const cur = new Array(m + 1).fill(0);
/* Base case is covered as we have initialized
the prev and cur arrays to 0.*/
for (let ind1 = 1; ind1 <= n; ind1++) {
for (let ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1[ind1 - 1] === str2[ind2 - 1])
cur[ind2] = 1 + prev[ind2 - 1];
else
cur[ind2] = Math.max(prev[ind2], cur[ind2 - 1]);
}
// Update the previous row with the current row
for (let i = 0; i <= m; i++) {
prev[i] = cur[i];
}
}
// Return the length of Longest Common Subsequence
return prev[m];
}
}
const s1 = "acd";
const s2 = "ced";
// Create an instance of Solution class
const sol = new Solution();
// Call the function to find and output
console.log("The Length of Longest Common Subsequence is", sol.lcs(s1, s2));
Complexity Analysis:
Time Complexity: O(N*M), N is the length of string S1 and M is the length of string S2. There are two nested loops which are running for N*M.Space Complexity:O(M), We are using an external array of size ‘M+1’ to store only two rows.
Frequently Occurring Doubts
Q: Why do we need a 2D DP table instead of a 1D DP array?
A: Each dp[i][j] depends on both dp[i-1][j] and dp[i][j-1], so we need to store LCS values for every prefix of str1 and str2.
Q: How can we optimize space from O(n × m) to O(min(n, m))?
A: Since dp[i][j] only depends on the previous row, we can use two rolling arrays (prev[] and curr[]), reducing space to O(min(n, m)).
Interview Followup Questions
Q: What if str1 and str2 were large, but had small alphabets?
A: Use bit masking (compressed DP) to track states efficiently.
Q: How can we optimize this problem to O(n log m) instead of O(n × m)?
A: Use Binary Search + Patience Sorting if the alphabet is limited.
Notes
Code
✅ Testcase
Input: {'m': '3', 'n': '5', 'str1': 'bdefg', 'str2': 'bfg'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting
Input: {'m': '3', 'n': '4', 'str1': 'mnop', 'str2': 'mnq'}
Expected:
2
2
Actual: -
Time: -
sec
Status: Waiting
Input: {'m': '4', 'n': '3', 'str1': 'abc', 'str2': 'dafb'}
Expected:
2
2
Actual: -
Time: -
sec
Status: Waiting