Intuition:
The first thing to understand is the condition for two asteroids to collide.
When does two asteroids collide?
We know that when two asteroids are moving in opposite direction, they collide. Now, there can be two cases of opposite moving asteroids:
- Moving apart from each other.
- Moving towards each other.
It is clear that the collision will only happen in the second case, i.e., when the asteroids are moving towards each other. This will happen when the first asteriod is moving towards right and later asteroid is moving towards left.
Now, in order to perform the collisions, only the left moving asteroids must be observed as all the earlier asteroids will be moving towards the right direction.
For every left moving asteroid, we must
first consider the asteroid that was found
last moving towards the right (because it will be the asteroid undergoing collision first). This gives an idea of using Stack data structure because it stores elements in LIFO fashion.
Now there can three scenarios that can arise during the collision:
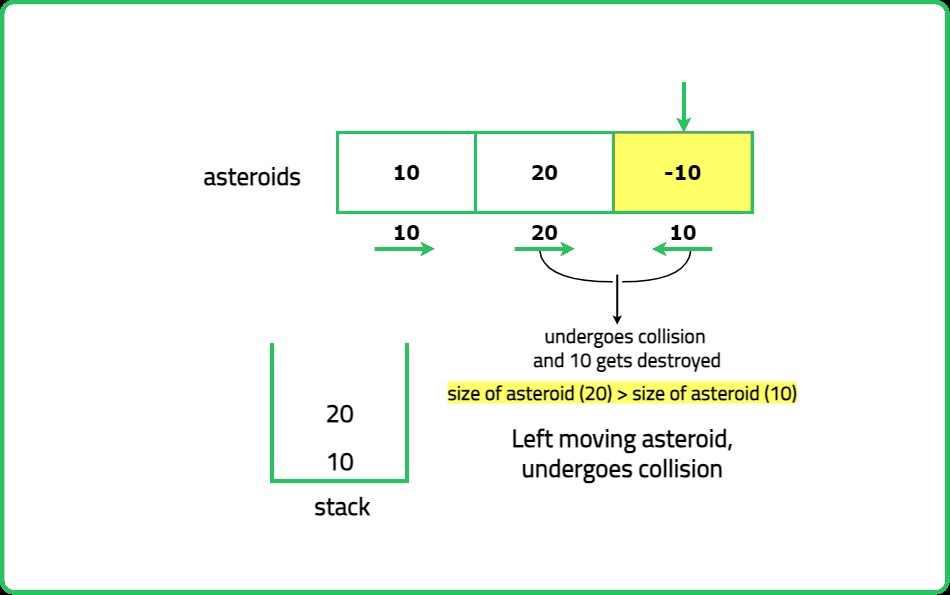
- The size of the right moving asteroid is more than the size of the left moving asteroid: In this case, the left moving asteroid will be destroyed leaving the right moving asteroird moving in the same direction.
- The size of the right moving asteroid is less than the size of the left moving asteroid: In this case, the right moving asteroid will be destroyed leaving the left moving asteroird moving in the same direction which may potentially collide with more asteroids.
- The sizes of the right moving asteroid and left moving asteroid are identical: In this case, both the asteroids will be destroyed leaving no asteroid from this collision.
Thus, all the right moving asteroids can be stored in the stack and for every right moving asteroid, collisions can be performed. Once the collision are done, any right or left moving asteroid will be left in the stack.
Modification:
Consider the following example:
![]()
(img yet to be inserted)
Here, once all the collisions happen, the answer is stored in the stack. But retrieving the elements from stack will return the elements in a reverse order. Hence, the elements must be reversed before returning the answer which takes extra time.
This can be avoided by
implementing the stack
using a list.
Approach:
- Create a stack (using list implementation) to keep track of the asteroids that are still in motion after potential collisions. Loop through each asteroid in the input array.
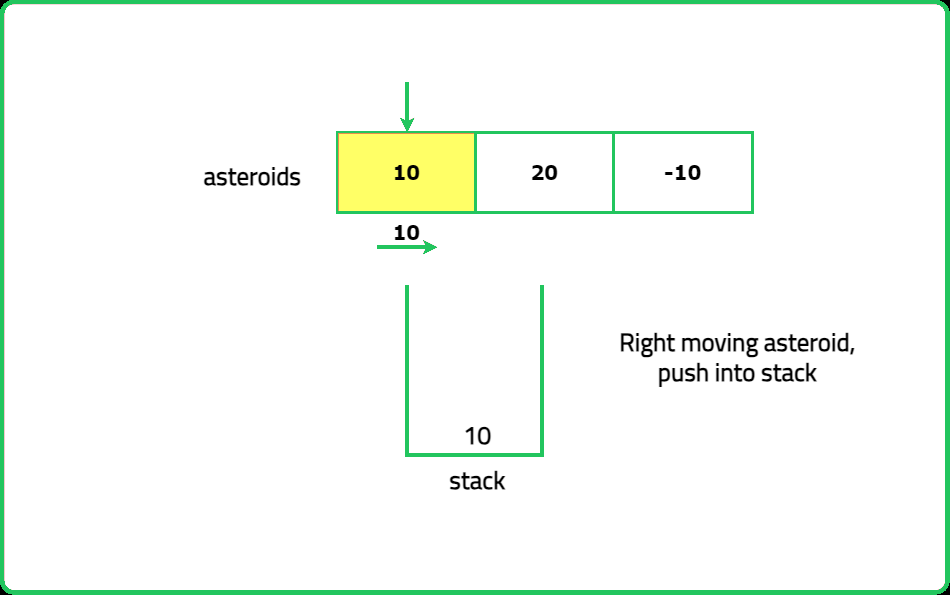
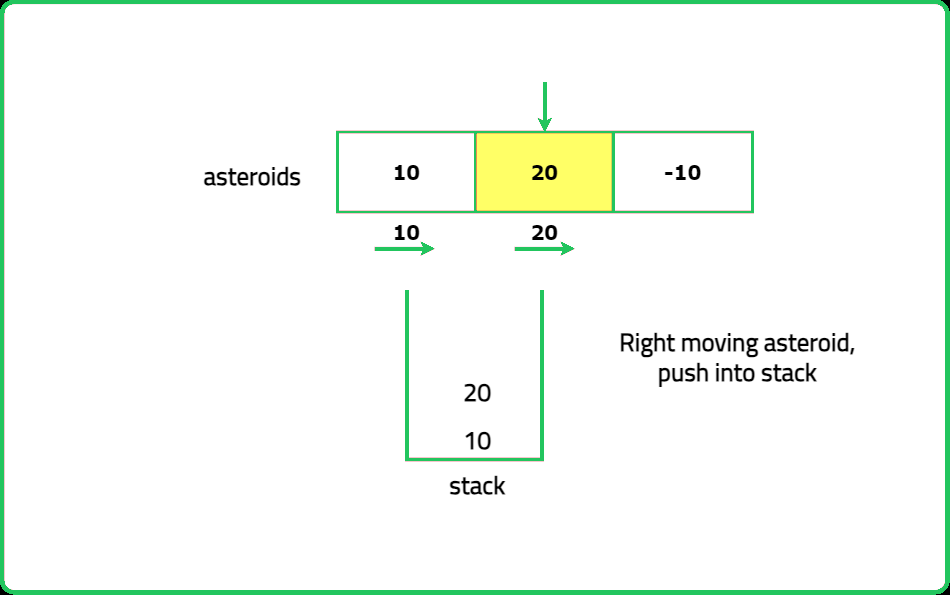
- Handling right moving asteroids: If the current asteroid is moving to the right (positive value), push it onto the stack.
- Handling left moving asteroids:
- If the current asteroid is moving to the left (negative value), compare it with the asteroids on the stack.
- Continue to compare and remove right-moving asteroids (positive values) from the stack if they are smaller in size than the current left-moving asteroid.
- If an asteroid on the stack has the same size as the current left-moving asteroid, remove both asteroids.
- If the stack becomes empty or the top of the stack is a left-moving asteroid (negative value), there will be no collision happening with the current left-moving asteroid. Hence, push the current left-moving asteroid onto the stack.
- After processing all asteroids, the stack will contain the state of the asteroids after all collisions. Return this as the final result.
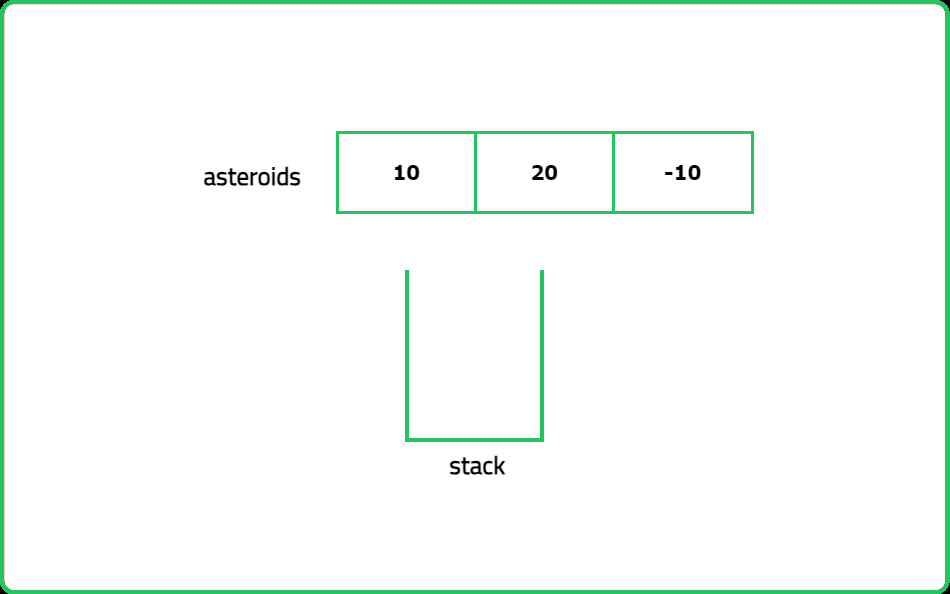
Dry Run:
Solution:
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to determine the state of
asteroids after all collisions */
vector<int> asteroidCollision(vector<int> &asteroids){
// Size of the array
int n = asteroids.size();
// List implementation of stack
vector<int> st;
// Traverse all the asteroids
for(int i=0; i < n; i++) {
/* Push the asteroid in stack if a
right moving asteroid is seen */
if(asteroids[i] > 0) {
st.push_back(asteroids[i]);
}
/* Else if the asteroid is moving
right, perform the collisions */
else {
/* Until the right moving asteroids are
smaller in size, keep on destroying them */
while(!st.empty() && st.back() > 0 &&
st.back() < abs(asteroids[i])) {
// Destroy the asteroid
st.pop_back();
}
/* If there is right moving asteroid
which is of same size */
if(!st.empty() &&
st.back() == abs(asteroids[i])) {
// Destroy both the asteroids
st.pop_back();
}
/* Otherwise, if there is no left
moving asteroid, the right moving
asteroid will not be destroyed */
else if(st.empty() ||
st.back() < 0){
// Storing the array in final state
st.push_back(asteroids[i]);
}
}
}
// Return the final state of asteroids
return st;
}
};
int main() {
vector<int> arr = {10, 20, -10};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to determine the state of
asteroids after all collisions */
vector<int> ans = sol.asteroidCollision(arr);
cout << "The state of asteroids after collisions is: ";
for(int i=0; i < ans.size(); i++) {
cout << ans[i] << " ";
}
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485
import java.util.*;
class Solution {
/* Function to determine the state of
asteroids after all collisions */
public int[] asteroidCollision(int[] asteroids) {
// Size of the array
int n = asteroids.length;
// List implementation of stack
List<Integer> st = new ArrayList<>();
// Traverse all the asteroids
for(int i = 0; i < n; i++) {
/* Push the asteroid in stack if a
right moving asteroid is seen */
if(asteroids[i] > 0) {
st.add(asteroids[i]);
}
/* Else if the asteroid is moving
left, perform the collisions */
else {
/* Until the right moving asteroids are
smaller in size, keep on destroying them */
while(!st.isEmpty() && st.get(st.size() - 1) > 0 &&
st.get(st.size() - 1) < Math.abs(asteroids[i])) {
// Destroy the asteroid
st.remove(st.size() - 1);
}
/* If there is right moving asteroid
which is of same size */
if(!st.isEmpty() &&
st.get(st.size() - 1) == Math.abs(asteroids[i])) {
// Destroy both the asteroids
st.remove(st.size() - 1);
}
/* Otherwise, if there is no left
moving asteroid, the right moving
asteroid will not be destroyed */
else if(st.isEmpty() ||
st.get(st.size() - 1) < 0){
// Storing the array in final state
st.add(asteroids[i]);
}
}
}
// Convert list to array
int[] result = new int[st.size()];
for(int i = 0; i < st.size(); i++) {
result[i] = st.get(i);
}
// Return the final state of asteroids
return result;
}
public static void main(String[] args) {
int[] arr = {10, 20, -10};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to determine the state of
asteroids after all collisions */
int[] ans = sol.asteroidCollision(arr);
System.out.print("The state of asteroids after collisions is: ");
for(int i = 0; i < ans.length; i++) {
System.out.print(ans[i] + " ");
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960
class Solution:
def asteroidCollision(self, asteroids):
# Size of the array
n = len(asteroids)
# List implementation of stack
st = []
# Traverse all the asteroids
for i in range(n):
# Push the asteroid in stack if a
# right moving asteroid is seen
if asteroids[i] > 0:
st.append(asteroids[i])
# Else if the asteroid is moving
# left, perform the collisions
else:
# Until the right moving asteroids are
# smaller in size, keep on destroying them
while (st and st[-1] > 0 and
st[-1] < abs(asteroids[i])):
# Destroy the asteroid
st.pop()
# If there is right moving asteroid
# which is of same size
if st and st[-1] == abs(asteroids[i]):
# Destroy both the asteroids
st.pop()
# Otherwise, if there is no left
# moving asteroid, the right moving
# asteroid will not be destroyed
elif not st or st[-1] < 0:
# Storing the array in final state
st.append(asteroids[i])
# Return the final state of asteroids
return st
# Main function to test the solution
if __name__ == "__main__":
arr = [10, 20, -10]
# Creating an instance of Solution class
sol = Solution()
# Function call to determine the state of
# asteroids after all collisions
ans = sol.asteroidCollision(arr)
print("The state of asteroids after collisions is:", ans)
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
class Solution {
/* Function to determine the state of
asteroids after all collisions */
asteroidCollision(asteroids) {
// Size of the array
let n = asteroids.length;
// List implementation of stack
let st = [];
// Traverse all the asteroids
for (let i = 0; i < n; i++) {
/* Push the asteroid in stack if a
right moving asteroid is seen */
if (asteroids[i] > 0) {
st.push(asteroids[i]);
}
/* Else if the asteroid is moving
left, perform the collisions */
else {
/* Until the right moving asteroids are
smaller in size, keep on destroying them */
while (st.length > 0 && st[st.length - 1] > 0 &&
st[st.length - 1] < Math.abs(asteroids[i])) {
// Destroy the asteroid
st.pop();
}
/* If there is right moving asteroid
which is of same size */
if (st.length > 0 &&
st[st.length - 1] == Math.abs(asteroids[i])) {
// Destroy both the asteroids
st.pop();
}
/* Otherwise, if there is no left
moving asteroid, the right moving
asteroid will not be destroyed */
else if (st.length == 0 ||
st[st.length - 1] < 0){
// Storing the array in final state
st.push(asteroids[i]);
}
}
}
// Return the final state of asteroids
return st;
}
}
// Main function to test the solution
const arr = [10, 20, -10];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to determine the state of
asteroids after all collisions */
const ans = sol.asteroidCollision(arr);
console.log("The state of asteroids after collisions is:", ans);
Complexity Analysis:
Time Complexity: O(N) (where N is the size of the asteroids array)
- Traversing all the asteroids takes O(N) time.
- Handling collisions:
- For each asteroid in the array, we may push or pop it from the stack at most once.
- The while loop checks the top of the stack and can pop elements from it. In the worst case, every asteroid can be pushed and popped from the stack once taking overall O(N) time.
Space Complexity: O(N)
In the worst case, all asteroids will be stored in the stack if there are no collisions, leading to a space requirement of O(N).