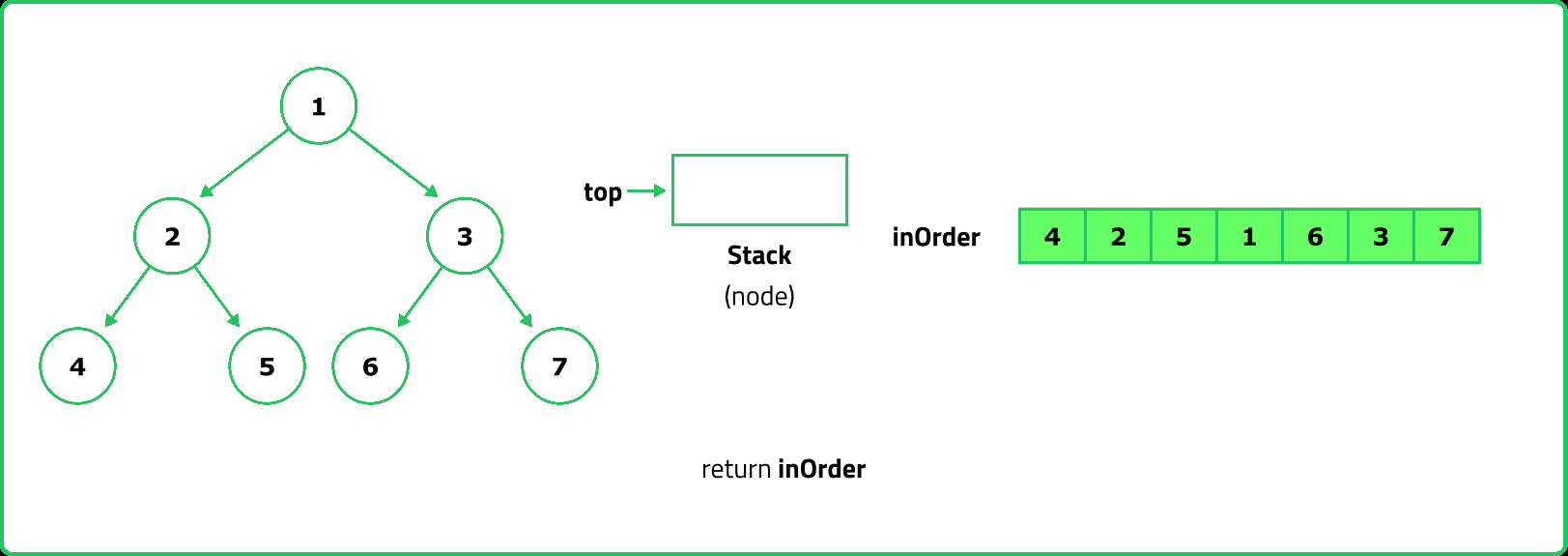
Inorder Traversal

Binary Trees Theory/Traversals Easy

Fun Fact: The Inorder traversal of a binary tree is commonly used in software development to process and manage hierarchical data structures, such as the Document Object Model (DOM) in web development
The DOM represents a web page so programs can change the document structure, style, and content
By using Inorder traversal, developers can efficiently access and manipulate elements on the webpage in the exact order they appear in the HTML markup, allowing for specific and efficient modifications to web content

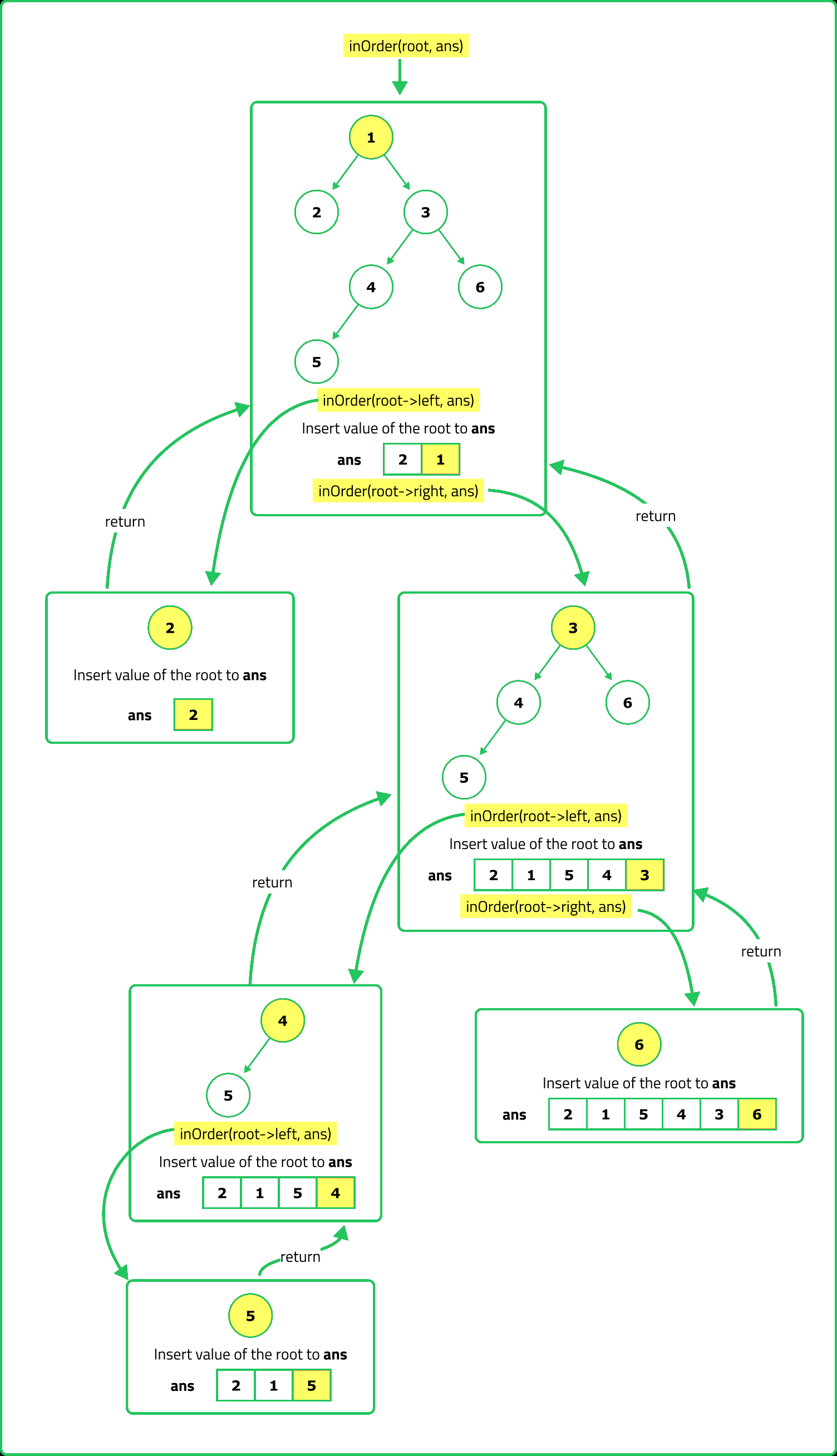
Given root of binary tree, return the Inorder traversal of the binary tree.

Examples:

Input : root = [1, 4, null, 4, 2]

Output : [4, 4, 2, 1]

Explanation :

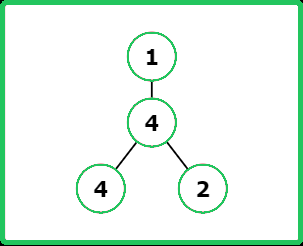
Input : root = [1, null, 2, 3]

Output : [1, 3, 2]

Explanation :

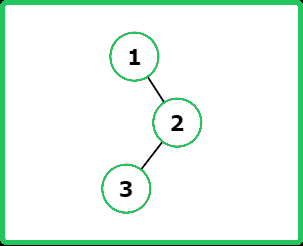
Input : root = [5, 1, 2, 8, null, 4, 5, null, 6]

Constraints

1 <= Number of Nodes <= 100
-100 Node.val <= 100

Hints

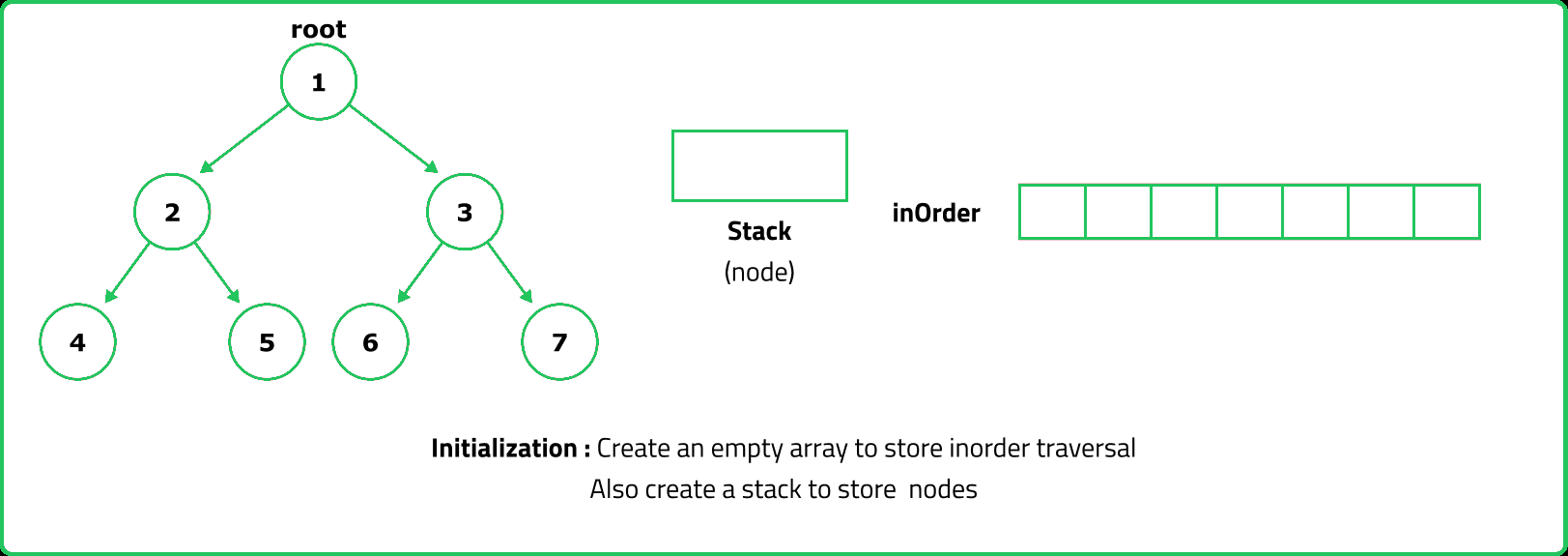
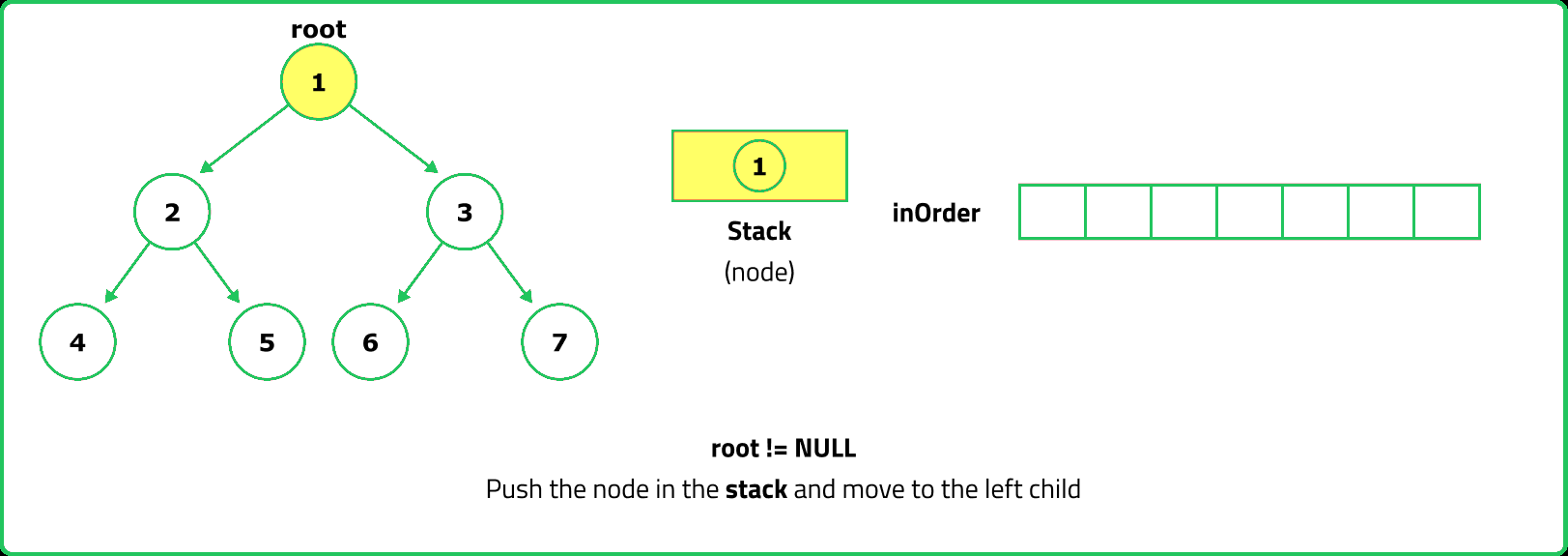
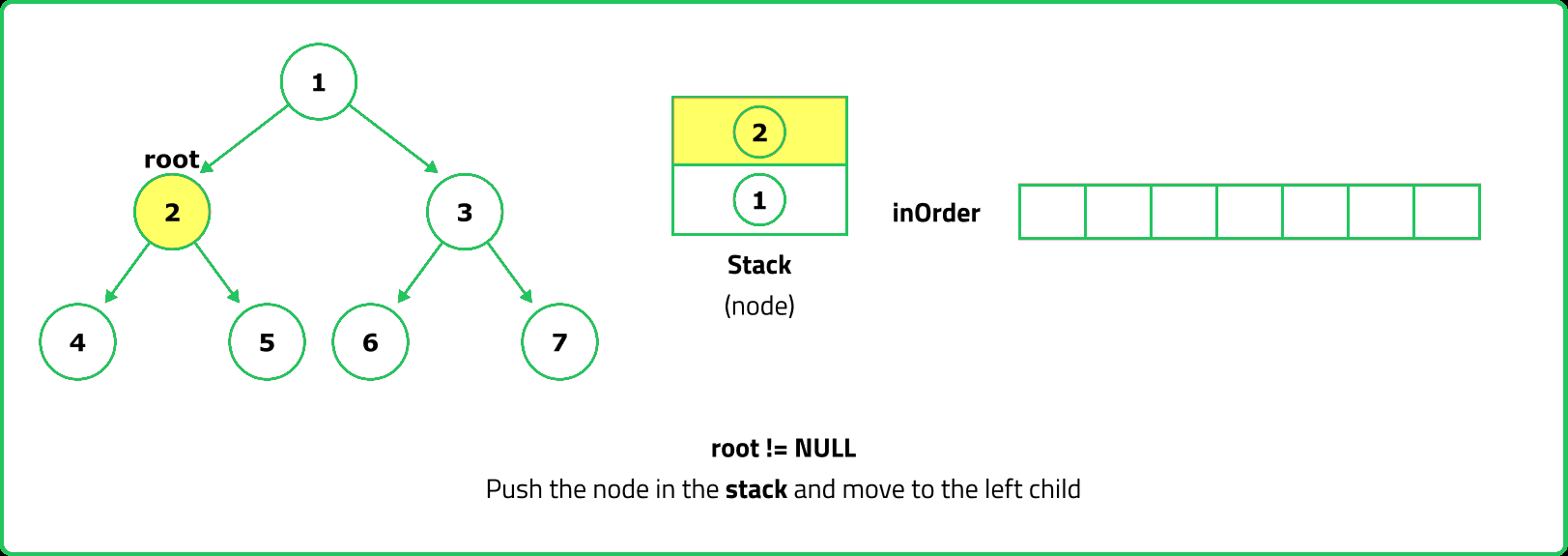
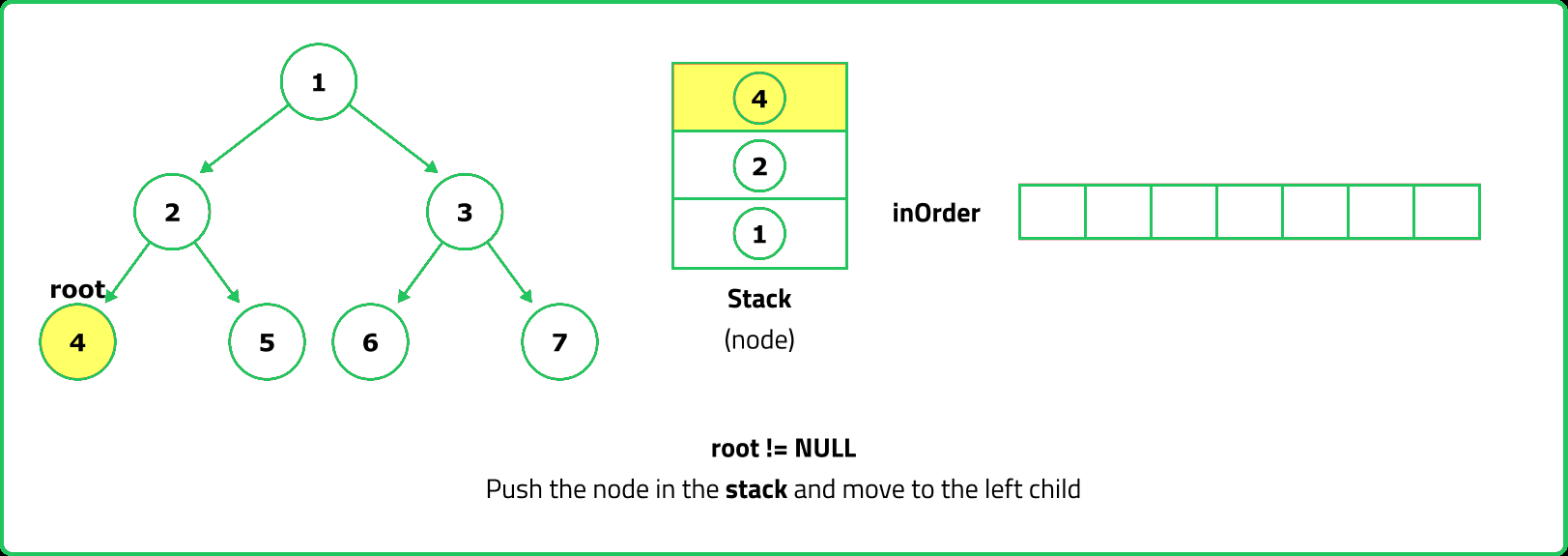
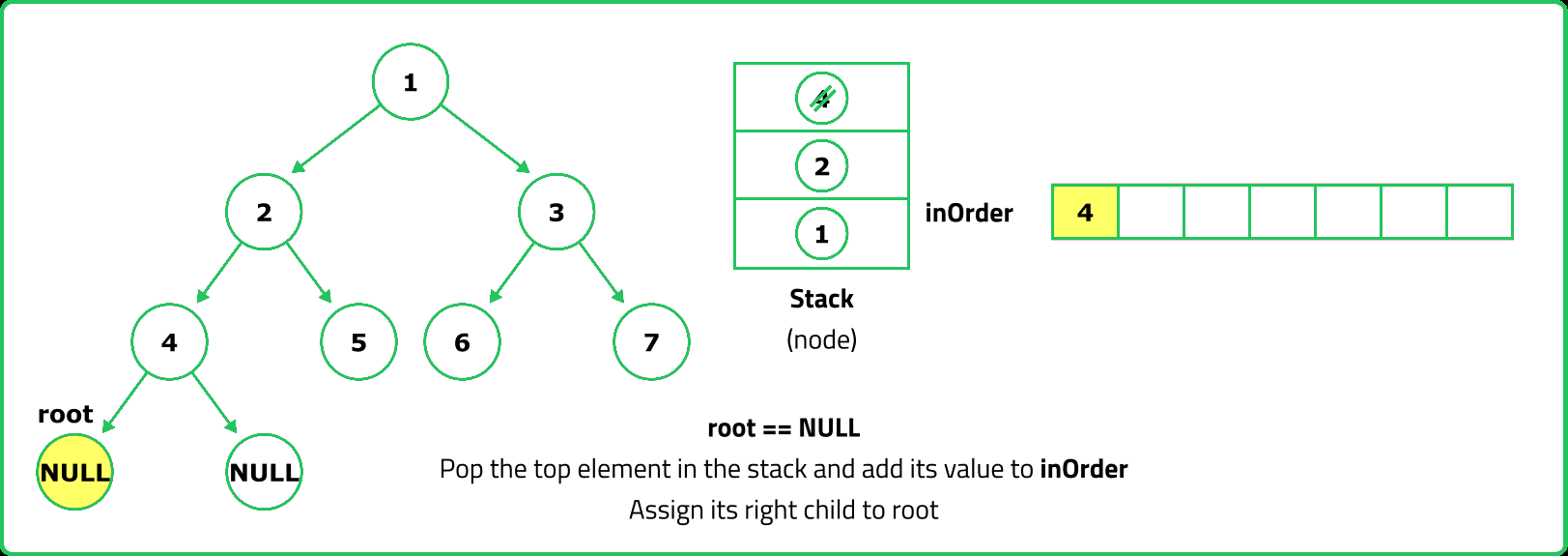
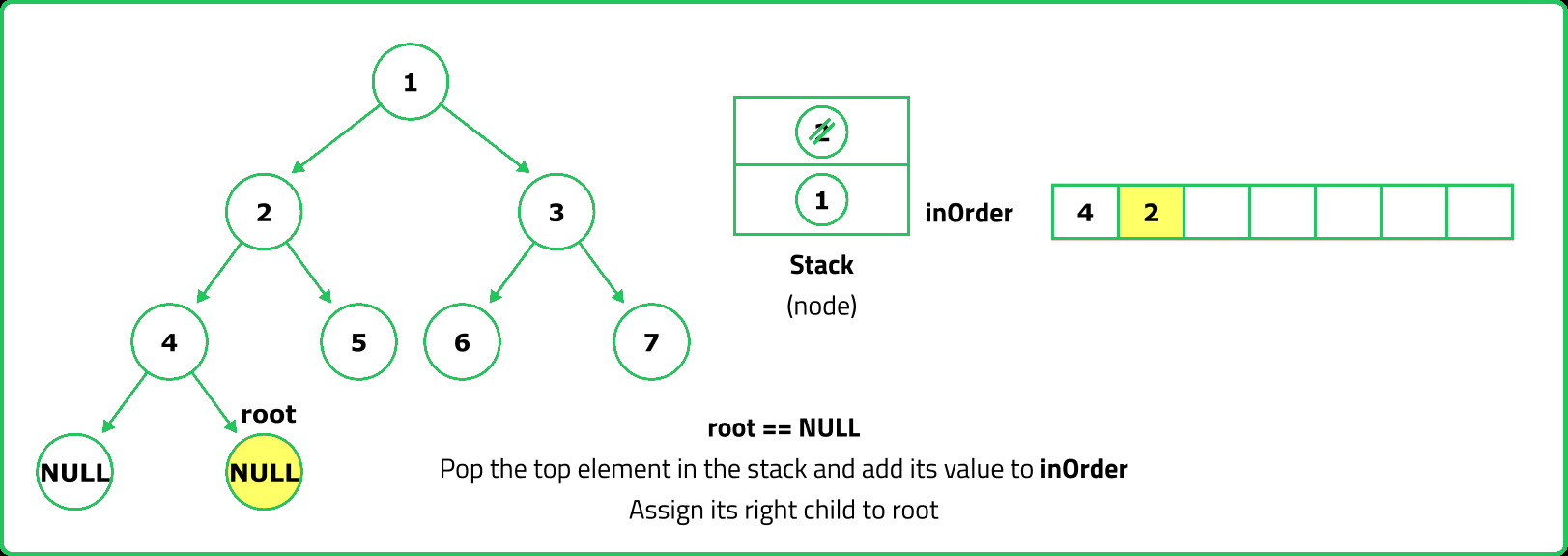
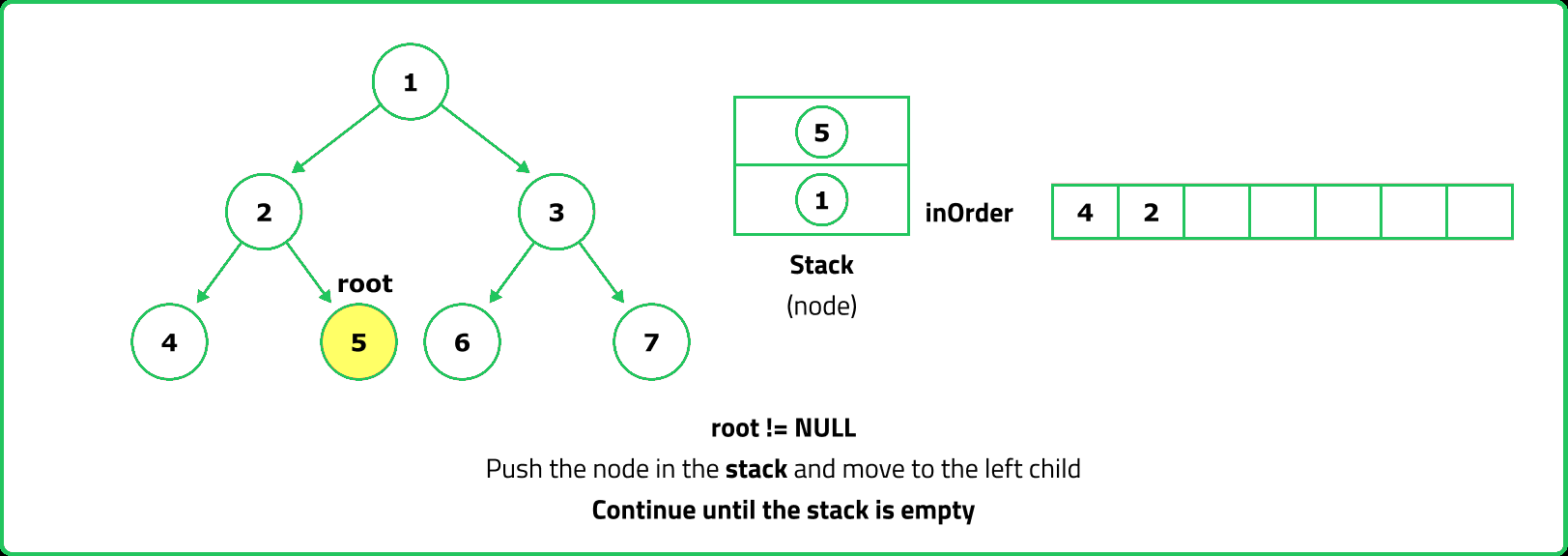
Since inorder traversal first visits the left subtree, we use a stack to store nodes while traversing left.
Push nodes onto the stack while moving left, process them, then move to their right child.

Company Tags

Broadcom ARM Seagate Technology Rockstar Games Freshworks Johnson & Johnson PayPal HashiCorp Medtronic Goldman Sachs Epic Games Flipkart Wayfair Snowflake Intel AMD Morgan Stanley Uber Airbnb Target Swiggy MongoDB Boston Consulting Group Reddit Bloomberg Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition

When we traverse a binary tree using inorder traversal, we follow a specific pattern: we visit the left subtree first, then the root node, and finally the right subtree. This order helps us systematically explore each node in the tree. The idea is to go as deep as possible into the left side of the tree before processing the nodes themselves and then moving to the right side.

Approach

To perform the inorder traversal, we follow these steps:

First, we check if the current node is null. If it is, we return because there is nothing to process.
If the current node is not null, we move to the left child of the current node and repeat the process.
Once we reach a node with no left child, we process the current node.
After processing the current node, we move to the right child and apply the same steps.

Algorithm

Base Case: If the current node is null, it means we have reached the end of a subtree and there are no further nodes to explore. Hence the recursive function stops and we return from that particular recursive call.

Recursive Function:

Traverse Left Subtree: Recursively traverse the left subtree by invoking the inorder function on the left child of the current node. This step continues the exploration of nodes in a depth-first manner.
Process Current Node: The recursive function begins by processing, i.e., adding to the array or printing the current node.
Traverse Right Subtree: After traversing the entire left subtree and then visiting the current node, we traverse the right subtree recursively. We once again invoke the inorder function, but this time on the right child of the current node.

Dry Run

#include <bits/stdc++.h>
using namespace std;

// TreeNode structure for the binary tree
struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;
    // Constructor to initialize
    // the TreeNode with a value
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

class Solution{
    private:
    // Function to perform inorder traversal
    // of the tree and store values in 'arr'
    void recursiveInorder(TreeNode* root, vector<int> &arr){
        // If the current Tree is NULL
        // (base case for recursion), return
        if(root == nullptr){
            return;
        }
        // Recursively traverse the left subtree
        recursiveInorder(root->left, arr);
        // Push the current TreeNode's
        // value into the vector
        arr.push_back(root->data);
        // Recursively traverse 
        // the right subtree
        recursiveInorder(root->right, arr);
    }
    
    public:
    // Function to initiate inorder traversal
    // and return the resulting vector
    vector<int> inorder(TreeNode* root){
        // Create an empty vector to
        // store inorder traversal values
        vector<int> arr;
        // Call the inorder traversal function
        recursiveInorder(root, arr);
        // Return the resulting vector
        // containing inorder traversal values
        return arr;
    }
};

// Main function
int main()
{
    // Creating a sample binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    
    Solution sol = Solution();
    // Getting inorder traversal
    vector<int> result = sol.inorder(root);

    // Displaying the inorder traversal result
    cout << "Inorder Traversal: ";
    // Output each value in the
    // inorder traversal result
    for(int val : result) {
        cout << val << " ";
    }
    cout << endl;

    return 0;
}
import java.util.ArrayList;
import java.util.List;

// TreeNode structure for the binary tree
class TreeNode {
    int data;
    TreeNode left;
    TreeNode right;

    // Constructor to initialize the TreeNode with a value
    TreeNode(int val) {
        data = val;
        left = null;
        right = null;
    }
}

class Solution {
    private void recursiveInorder(TreeNode root, List<Integer> arr) {
        // If the current Tree is NULL (base case for recursion), return
        if (root == null) {
            return;
        }
        // Recursively traverse the left subtree
        recursiveInorder(root.left, arr);
        // Push the current TreeNode's value into the vector
        arr.add(root.data);
        // Recursively traverse the right subtree
        recursiveInorder(root.right, arr);
    }

    // Function to initiate inorder traversal and return the resulting vector
    public List<Integer> inorder(TreeNode root) {
        // Create an empty vector to store inorder traversal values
        List<Integer> arr = new ArrayList<>();
        // Call the inorder traversal function
        recursiveInorder(root, arr);
        // Return the resulting vector containing inorder traversal values
        return arr;
    }

    public static void main(String[] args) {
        // Creating a sample binary tree
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        Solution sol = new Solution();
        // Getting inorder traversal
        List<Integer> result = sol.inorder(root);

        // Displaying the inorder traversal result
        System.out.print("Inorder Traversal: ");
        // Output each value in the inorder traversal result
        for (int val : result) {
            System.out.print(val + " ");
        }
        System.out.println();
    }
}
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.data = val
        self.left = left
        self.right = right

class Solution:
    def __init__(self):
        pass

    def recursiveInorder(self, root, arr):
        # If the current Tree is NULL (base case for recursion), return
        if root is None:
            return
        # Recursively traverse the left subtree
        self.recursiveInorder(root.left, arr)
        # Push the current TreeNode's value into the vector
        arr.append(root.data)
        # Recursively traverse the right subtree
        self.recursiveInorder(root.right, arr)

    # Function to initiate inorder traversal and return the resulting vector
    def inorder(self, root):
        # Create an empty vector to store inorder traversal values
        arr = []
        # Call the inorder traversal function
        self.recursiveInorder(root, arr)
        # Return the resulting vector containing inorder traversal values
        return arr

if __name__ == "__main__":
    # Creating a sample binary tree
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)

    sol = Solution()
    # Getting inorder traversal
    result = sol.inorder(root)

    # Displaying the inorder traversal result
    print("Inorder Traversal: ", end="")
    # Output each value in the inorder traversal result
    for val in result:
        print(val, end=" ")
    print()
// TreeNode structure for the binary tree
class TreeNode {
    constructor(val) {
        this.data = val;
        this.left = null;
        this.right = null;
    }
}

class Solution {
    // Function to perform inorder traversal
    // of the tree and store values in 'arr'
    recursiveInorder(root, arr) {
        // If the current Tree is NULL (base case for recursion), return
        if (root === null) {
            return;
        }
        // Recursively traverse the left subtree
        this.recursiveInorder(root.left, arr);
        // Push the current TreeNode's value into the vector
        arr.push(root.data);
        // Recursively traverse the right subtree
        this.recursiveInorder(root.right, arr);
    }

    // Function to initiate inorder traversal and return the resulting vector
    inorder(root) {
        // Create an empty vector to store inorder traversal values
        const arr = [];
        // Call the inorder traversal function
        this.recursiveInorder(root, arr);
        // Return the resulting vector containing inorder traversal values
        return arr;
    }
}

// Main function
function main() {
    // Creating a sample binary tree
    const root = new TreeNode(1);
    root.left = new TreeNode(2);
    root.right = new TreeNode(3);
    root.left.left = new TreeNode(4);
    root.left.right = new TreeNode(5);

    const sol = new Solution();
    // Getting inorder traversal
    const result = sol.inorder(root);

    // Displaying the inorder traversal result
    console.log("Inorder Traversal: ", result.join(" "));
}

main();

Complexity Analysis

Time Complexity O(N) where n is the number of nodes in the tree due to traversal of each node once

SpaceComplexity O(h) where h is the height of the tree for the recursion stack, plus O(n) for the output array

Intuition

When we think about traversing a binary tree, the recursive approach might come to mind first. However, there's an alternative method that involves iterating through the tree step by step, which can be more efficient in certain scenarios. This iterative method allows us to manually control the traversal process, ensuring that we visit each node in the correct order: first exploring the left side of the tree, then processing the current node, and finally exploring the right side. By doing this, we avoid the overhead that comes with recursion, such as managing the call stack. This approach can be particularly helpful in environments with limited memory or when dealing with very large trees, as it allows for more fine-tuned control over the traversal process.

Approach

The iterative approach to inorder traversal uses a stack to mimic the behavior of recursion. By using a stack, we can keep track of nodes we need to process, allowing us to traverse the tree without the need for recursive calls. This approach follows the inorder sequence: visit the left subtree, process the root, and then visit the right subtree. The stack helps manage this sequence effectively by storing nodes as we traverse down the left side of the tree and then processing them in the correct order.

Algorithm

To perform the iterative inorder traversal, follow these steps:

Step 1: Initialize an empty stack and set the current node to the root of the binary tree.
Step 2: Enter a loop that continues as long as there are nodes in the stack or the current node is not null.
Step 3: If the current node is not null, push it onto the stack and move to its left child. Repeat this step until you reach a node with no left child.
Step 4: If the current node is null, pop the top node from the stack, process it by adding its value to the result array, and then move to its right child.
Step 5: Repeat steps 3 and 4 until the stack is empty and the current node is null.
Step 6: Return the result array containing the inorder traversal of the binary tree.

Dry Run

#include <bits/stdc++.h>
using namespace std;

// Define the TreeNode structure
struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : data(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
// Function to perform inorder traversal
// of a binary tree iteratively
vector<int> inorder(TreeNode* root){
    // Initialize a stack to track nodes
    stack<TreeNode*> st;
    // Start from the root node
    TreeNode* node = root;
    // Initialize a vector to store
    // inorder traversal result
    vector<int> inorder;

    // Start an infinite
    // loop for traversal
    while(true){
        // If the current node is not NULL
        if(node != NULL){
            // Push the current
            // node to the stack
            st.push(node);
            // Move to the left child
            // of the current node
            node = node->left;
        }
        else{
            // If the stack is empty,
            // break the loop
            if(st.empty()){
                break;
            }
            // Retrieve a node from the stack
            node = st.top();
            // Remove the node from the stack
            st.pop();
            // Add the node's value to
            // the inorder traversal list
            inorder.push_back(node->data);
            // Move to the right child
            // of the current node
            node = node->right;
        }
    }
    // Return the inorder
    // traversal result
    return inorder;
}

};

int main() {
    // Creating a binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    // Initializing the Solution class
    Solution sol;

    // Getting the inorder traversal
    vector<int> result = sol.inorder(root);

    // Displaying the inorder traversal result
    cout << "Inorder Traversal: ";
    for (int val : result) {
        cout << val << " ";
    }
    cout << endl;

    return 0;
}

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

// Define the TreeNode structure
class TreeNode {
    int data;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { data = x; left = null; right = null; }
}

class Solution {
    // Function to perform inorder traversal
    // of a binary tree iteratively
    public List<Integer> inorder(TreeNode root) {
        // Initialize a stack to track nodes
        Stack<TreeNode> st = new Stack<>();
        // Start from the root node
        TreeNode node = root;
        // Initialize a list to store
        // inorder traversal result
        List<Integer> inorder = new ArrayList<>();

        // Start an infinite
        // loop for traversal
        while (true) {
            // If the current node is not NULL
            if (node != null) {
                // Push the current
                // node to the stack
                st.push(node);
                // Move to the left child
                // of the current node
                node = node.left;
            } else {
                // If the stack is empty,
                // break the loop
                if (st.isEmpty()) {
                    break;
                }
                // Retrieve a node from the stack
                node = st.pop();
                // Add the node's value to
                // the inorder traversal list
                inorder.add(node.data);
                // Move to the right child
                // of the current node
                node = node.right;
            }
        }
        // Return the inorder
        // traversal result
        return inorder;
    }

    public static void main(String[] args) {
        // Creating a binary tree
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        // Initializing the Solution class
        Solution sol = new Solution();

        // Getting the inorder traversal
        List<Integer> result = sol.inorder(root);

        // Displaying the inorder traversal result
        System.out.print("Inorder Traversal: ");
        for (int val : result) {
            System.out.print(val + " ");
        }
        System.out.println();
    }
}
# Define the TreeNode structure
class TreeNode:
    def __init__(self, x):
        self.data = x
        self.left = None
        self.right = None

class Solution:
    # Function to perform inorder traversal
    # of a binary tree iteratively
    def inorder(self, root):
        # Initialize a stack to track nodes
        st = []
        # Start from the root node
        node = root
        # Initialize a list to store
        # inorder traversal result
        inorder = []

        # Start an infinite
        # loop for traversal
        while True:
            # If the current node is not NULL
            if node is not None:
                # Push the current
                # node to the stack
                st.append(node)
                # Move to the left child
                # of the current node
                node = node.left
            else:
                # If the stack is empty,
                # break the loop
                if not st:
                    break
                # Retrieve a node from the stack
                node = st.pop()
                # Add the node's value to
                # the inorder traversal list
                inorder.append(node.data)
                # Move to the right child
                # of the current node
                node = node.right
        
        # Return the inorder
        # traversal result
        return inorder

# Creating a binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

# Initializing the Solution class
sol = Solution()

# Getting the inorder traversal
result = sol.inorder(root)

# Displaying the inorder traversal result
print("Inorder Traversal:", result)
// Define the TreeNode structure
class TreeNode {
    constructor(val) {
        this.data = val;
        this.left = null;
        this.right = null;
    }
}

class Solution {
    // Function to perform inorder traversal
    // of a binary tree iteratively
    inorder(root) {
        // Initialize a stack to track nodes
        const st = [];
        // Start from the root node
        let node = root;
        // Initialize an array to store
        // inorder traversal result
        const inorder = [];

        // Start an infinite
        // loop for traversal
        while (true) {
            // If the current node is not NULL
            if (node !== null) {
                // Push the current
                // node to the stack
                st.push(node);
                // Move to the left child
                // of the current node
                node = node.left;
            } else {
                // If the stack is empty,
                // break the loop
                if (st.length === 0) {
                    break;
                }
                // Retrieve a node from the stack
                node = st.pop();
                // Add the node's value to
                // the inorder traversal list
                inorder.push(node.data);
                // Move to the right child
                // of the current node
                node = node.right;
            }
        }
        // Return the inorder
        // traversal result
        return inorder;
    }
}

// Creating a binary tree
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);

// Initializing the Solution class
const sol = new Solution();

// Getting the inorder traversal
const result = sol.inorder(root);

// Displaying the inorder traversal result
console.log("Inorder Traversal:", result);

Complexity Analysis

Time Complexity O(N) since each node is processed once in a binary tree

SpaceComplexity O(h) where h is the height of the binary tree, for the stack and the result list

Code

Problem List

Inorder Traversal

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Approach

Algorithm

Dry Run

Complexity Analysis

Intuition

Approach

Algorithm

Dry Run

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code