Union of two sorted arrays
Arrays
Logic Building
Easy
- This type of problem is often used in database management systems and search engines for combining and analyzing large data sets
- Particularly, it serves as the underlying concept for SQL's UNION operation which helps in merging data from two SQL tables while removing duplicates
- Additionally, search engine algorithms use similar concepts to combine search results from various sources into one single, sorted and non-repetitive result set
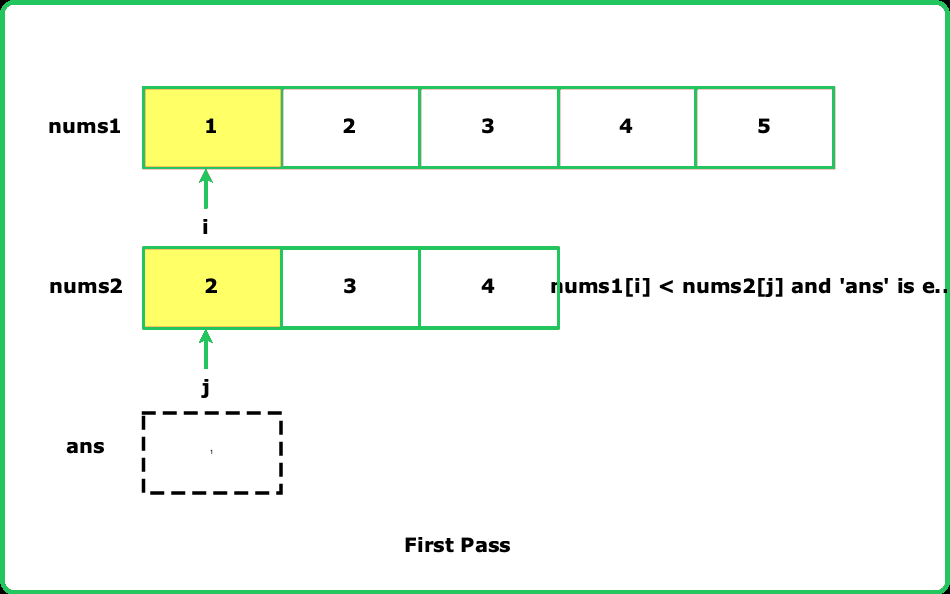
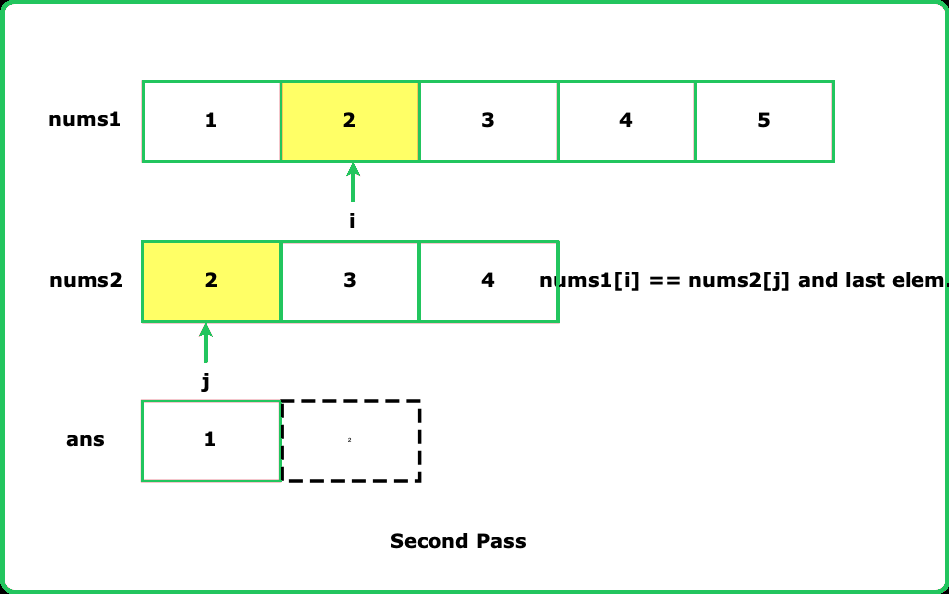
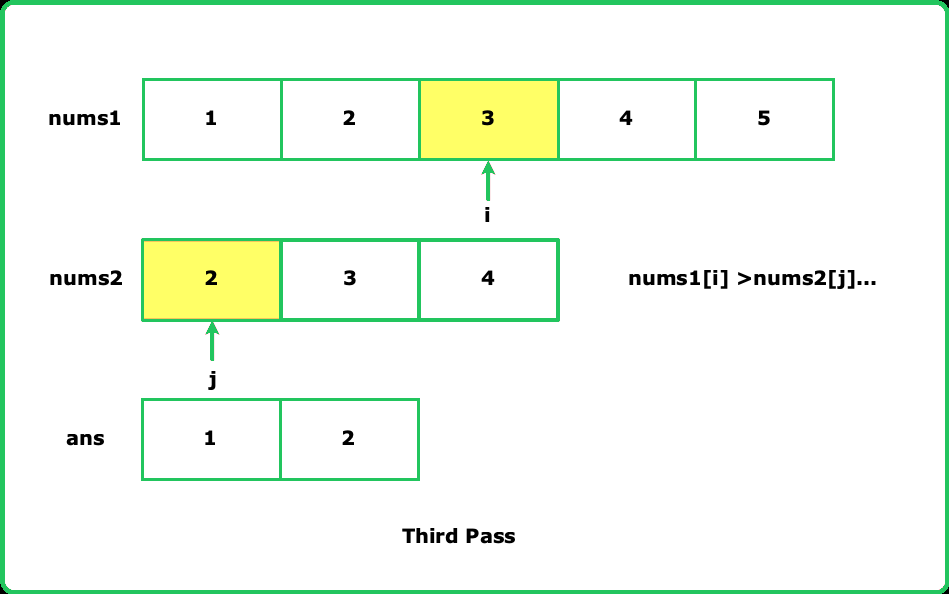
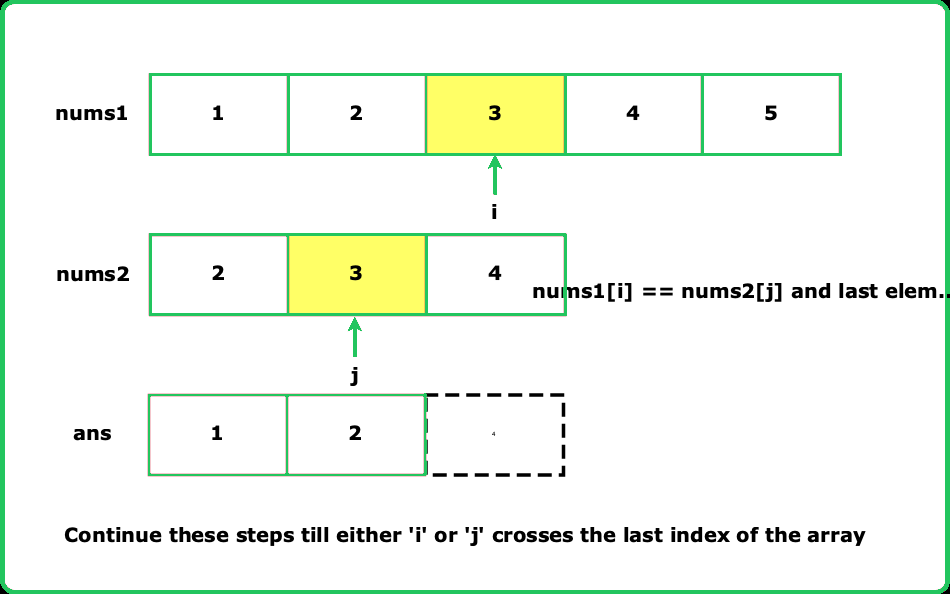
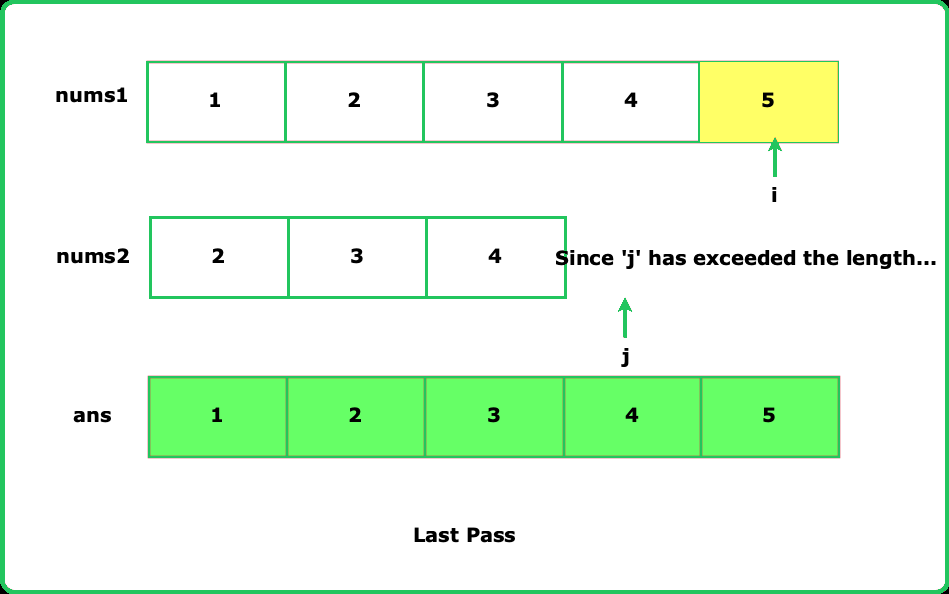
Given two sorted arrays nums1 and nums2, return an array that contains the union of these two arrays. The elements in the union must be in ascending order.
The union of two arrays is an array where all values are distinct and are present in either the first array, the second array, or both.
Examples:
Input: nums1 = [1, 2, 3, 4, 5], nums2 = [1, 2, 7]
Output: [1, 2, 3, 4, 5, 7]
Explanation: The elements 1, 2 are common to both, 3, 4, 5 are from nums1 and 7 is from nums2
Input: nums1 = [3, 4, 6, 7, 9, 9], nums2 = [1, 5, 7, 8, 8]
Output: [1, 3, 4, 5, 6, 7, 8, 9]
Explanation: The element 7 is common to both, 3, 4, 6, 9 are from nums1 and 1, 5, 8 is from nums2
Input: nums1 = [3, 4, 4, 4], nums2 = [6, 7, 7]
Constraints
- 1 <= nums1.length, nums2.length <= 1000
- -104 <= nums1[i] , nums2[i] <= 104
- Both nums1 and nums2 are sorted in non-decreasing order
Hints
- Utilize two pointers to traverse the sorted arrays simultaneously. This helps efficiently handle duplicates and maintain ascending order.
- Since both arrays are sorted, you can skip elements that are equal to the last added element in the union array.
Company Tags
Lyft
Riot Games
Swiggy
Johnson & Johnson
Salesforce
Byju's
Chewy
GE Healthcare
Pinterest
Morgan Stanley
Databricks
Micron Technology
Freshworks
Activision Blizzard
Qualcomm
eBay
KPMG
Medtronic
Airbnb
Walmart
Zynga
Shopify
Boston Consulting Group
HashiCorp
Stripe
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro