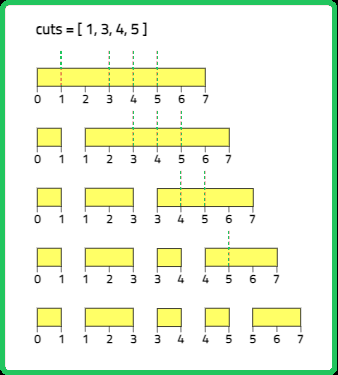
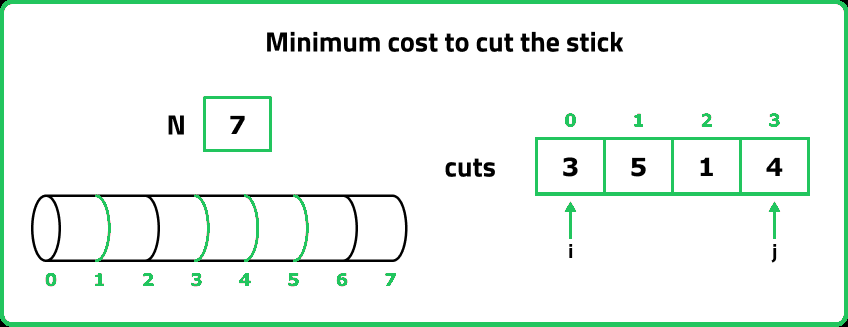
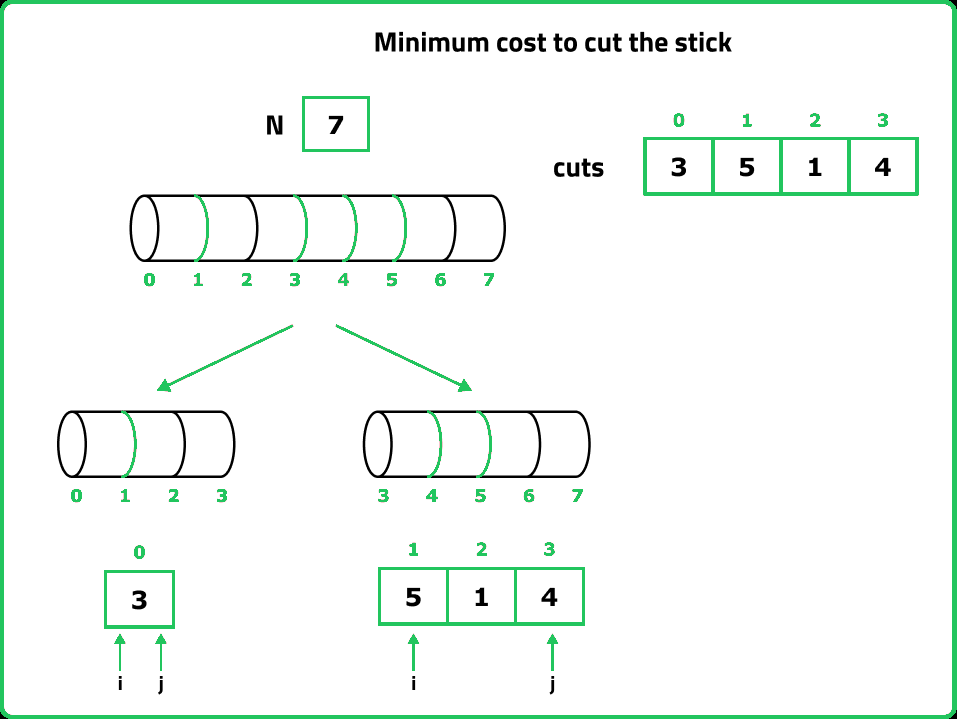
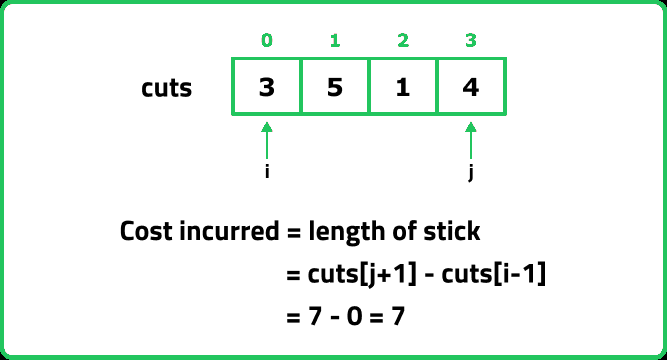
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
// Function to calculate the minimum cost incurred
int func(int i, int j, vector<int> &cuts, vector<vector<int>> &dp) {
/* Base case: If i is greater than
j, there are no cuts to consider.*/
if (i > j) {
return 0;
}
//Check if the subproblem is already solved
if (dp[i][j] != -1) {
return dp[i][j];
}
int mini = INT_MAX;
for (int ind = i; ind <= j; ind++) {
/* Calculate the cost for
making a cut at position 'ind'.*/
int ans = cuts[j + 1] - cuts[i - 1] + func(i, ind - 1, cuts, dp) + func(ind + 1, j, cuts, dp);
mini = min(mini, ans);
}
//Return the result
return dp[i][j] = mini;
}
public:
// Function to compute the minimum cost
int minCost(int n, vector<int> &cuts) {
int c = cuts.size();
/* Modify the cuts array by adding 0
at the beginning and 'n' at the end.*/
cuts.push_back(n);
cuts.insert(cuts.begin(), 0);
sort(cuts.begin(), cuts.end());
// Create a DP table to store calculated values.
vector<vector<int>> dp(c + 1, vector<int>(c + 1, -1));
// Call the recursive function to find minimum cost.
return func(1, c, cuts, dp);
}
};
int main() {
vector<int> cuts = {3, 5, 1, 4};
int n = 7;
//Create an instance of Solution class
Solution sol;
cout << "The minimum cost incurred is: " << sol.minCost(n, cuts) << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
import java.util.*;
class Solution {
// Function to calculate the minimum cost incurred
private int func(int i, int j, int[] cuts, int[][] dp) {
/* Base case: If i is greater than
j, there are no cuts to consider.*/
if (i > j) {
return 0;
}
// Check if the subproblem is already solved
if (dp[i][j] != -1) {
return dp[i][j];
}
int mini = Integer.MAX_VALUE;
for (int ind = i; ind <= j; ind++) {
/* Calculate the cost for
making a cut at position 'ind'.*/
int ans = cuts[j + 1] - cuts[i - 1] + func(i, ind - 1, cuts, dp) + func(ind + 1, j, cuts, dp);
mini = Math.min(mini, ans);
}
// Return the result
return dp[i][j] = mini;
}
// Function to compute the minimum cost
public int minCost(int n, List<Integer> cuts) {
int c = cuts.size();
/* Convert List<Integer> to int[] */
int[] newCuts = new int[c + 2];
newCuts[0] = 0;
for (int i = 0; i < c; i++) {
newCuts[i + 1] = cuts.get(i);
}
newCuts[c + 1] = n;
Arrays.sort(newCuts);
// Create a DP table to store calculated values.
int[][] dp = new int[c + 1][c + 1];
for (int[] row : dp) {
Arrays.fill(row, -1);
}
// Call the recursive function to find minimum cost.
return func(1, c, newCuts, dp);
}
public static void main(String[] args) {
List<Integer> cuts = new ArrayList<>();
cuts.add(3);
cuts.add(5);
cuts.add(1);
cuts.add(4);
int n = 7;
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("The minimum cost incurred is: " + sol.minCost(n, cuts));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
class Solution:
# Function to calculate the minimum cost incurred
def func(self, i, j, cuts, dp):
""" Base case: If i is greater than
j, there are no cuts to consider."""
if i > j:
return 0
# Check if the subproblem is already solved
if dp[i][j] != -1:
return dp[i][j]
mini = float('inf')
for ind in range(i, j + 1):
""" Calculate the cost for
making a cut at position 'ind'."""
ans = cuts[j + 1] - cuts[i - 1] + self.func(i, ind - 1, cuts, dp) + self.func(ind + 1, j, cuts, dp)
mini = min(mini, ans)
# Return the result
dp[i][j] = mini
return mini
# Function to compute the minimum cost
def minCost(self, n, cuts):
c = len(cuts)
""" Modify the cuts array by adding 0
at the beginning and 'n' at the end."""
cuts = [0] + sorted(cuts) + [n]
# Create a DP table to store calculated values.
dp = [[-1] * (c + 2) for _ in range(c + 2)]
# Call the recursive function to find minimum cost.
return self.func(1, c, cuts, dp)
if __name__ == "__main__":
cuts = [3, 5, 1, 4]
n = 7
# Create an instance of Solution class
sol = Solution()
print("The minimum cost incurred is:", sol.minCost(n, cuts))
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051
class Solution {
// Function to calculate the minimum cost incurred
func(i, j, cuts, dp) {
/* Base case: If i is greater than
j, there are no cuts to consider.*/
if (i > j) {
return 0;
}
// Check if the subproblem is already solved
if (dp[i][j] !== -1) {
return dp[i][j];
}
let mini = Number.MAX_VALUE;
for (let ind = i; ind <= j; ind++) {
/* Calculate the cost for
making a cut at position 'ind'.*/
let ans = cuts[j + 1] - cuts[i - 1] + this.func(i, ind - 1, cuts, dp) + this.func(ind + 1, j, cuts, dp);
mini = Math.min(mini, ans);
}
// Return the result
dp[i][j] = mini;
return mini;
}
// Function to compute the minimum cost
minCost(n, cuts) {
let c = cuts.length;
/* Modify the cuts array by adding 0
at the beginning and 'n' at the end.*/
cuts = [0, ...cuts.sort((a, b) => a - b), n];
// Create a DP table to store calculated values.
let dp = Array.from({ length: c + 1 }, () => Array(c + 1).fill(-1));
// Call the recursive function to find minimum cost.
return this.func(1, c, cuts, dp);
}
}
const cuts = [3, 5, 1, 4];
const n = 7;
// Create an instance of Solution class
const sol = new Solution();
console.log("The minimum cost incurred is:", sol.minCost(n, cuts));