Diameter of Binary Tree
Binary Trees
Medium Problems
Medium
- The concept underlying the Diameter of Binary Tree problem is used in practical software development, notably in the field of Network Routing Algorithms
- These algorithms use the principles of tree traversal and diameter calculation to determine the most efficient path for data to travel between nodes in a network
- Understanding the longest path or "diameter" helps engineers and developers optimize these paths and enhance the overall efficiency of the network
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in the tree. It may or may not pass through the root.
Examples:
Input : root = [1, 2, 3, 4, 5]
Output : 3
Explanation : The path length between node 4 and 3 is of length 3.
There are other ways to reach the solution.
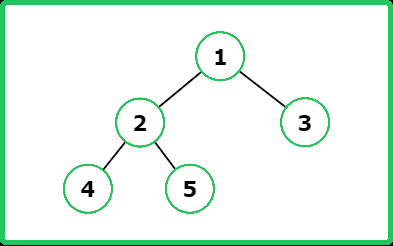
Input : root = [1, 2, 3, null, 4, null, 5]
Output : 4
Explanation : The path length between node 4 and 5 is of length 4.
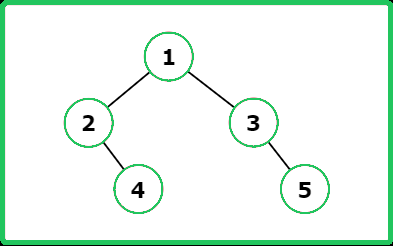
Input : root = [5, 1, 2, 8, 3, null, 5, null, 4]
Constraints
- 1 <= Number of Nodes 104
- -100 <= Node.val <= 100
Hints
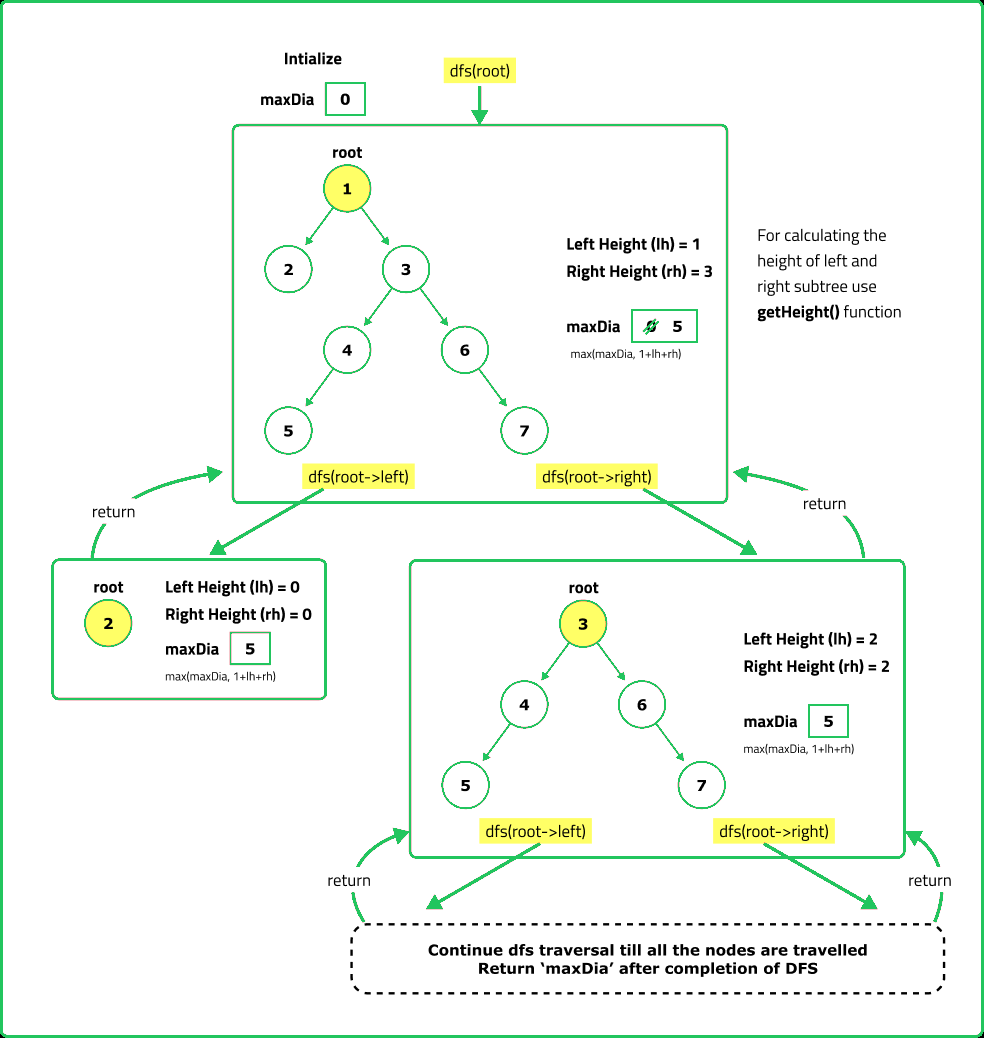
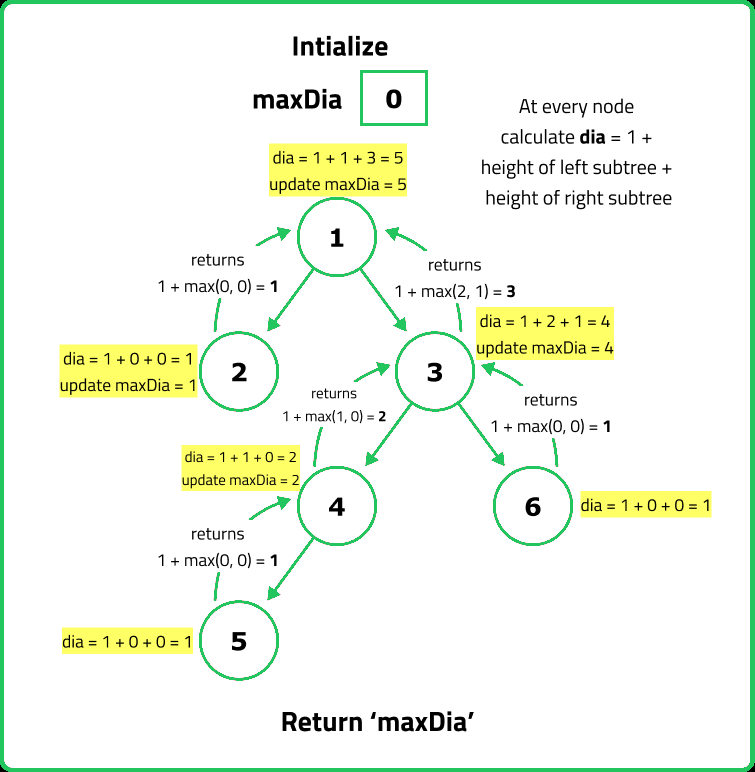
- A naive approach computes the height separately for each node and calculates the possible diameter at each step, leading to an O(n²) time complexity (height computation is O(n) at each of the O(n) nodes).
- An optimized approach computes height while finding the diameter, reducing the time complexity to O(n). This is done by modifying the recursive function to return both the height of the subtree and current max diameter at each step.
Company Tags
Intel
Alibaba
Swiggy
Freshworks
Electronic Arts
Optum
Reddit
PayPal
Stripe
Visa
Qualcomm
Siemens Healthineers
Robinhood
Byju's
Deloitte
NVIDIA
Wayfair
Airbnb
Rakuten
Mastercard
Snowflake
OYO Rooms
Splunk
Bloomberg
GE Healthcare
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe