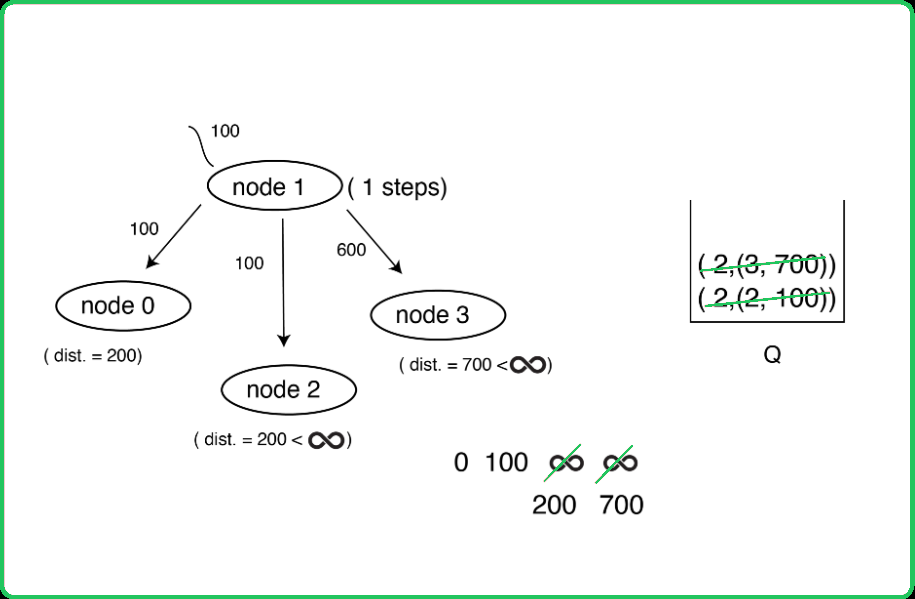
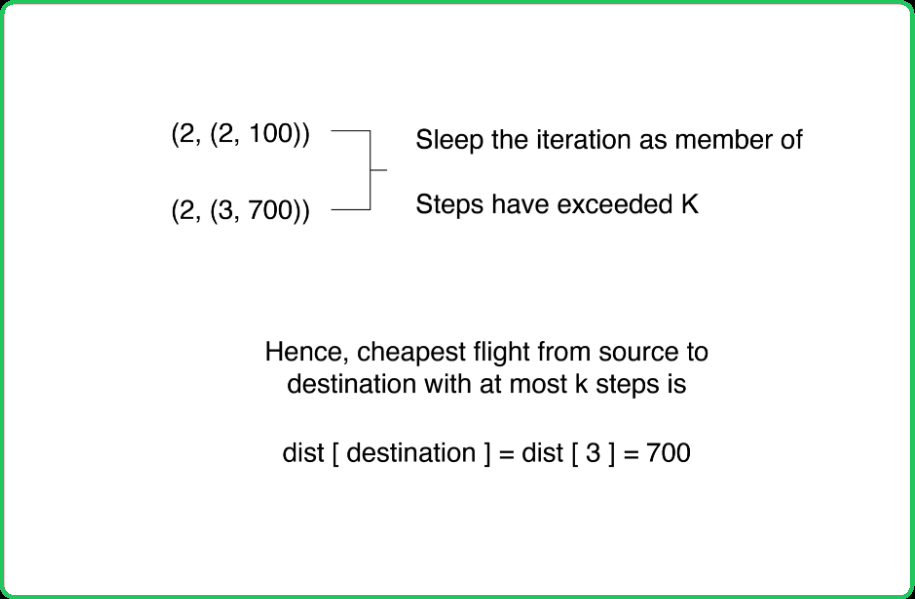
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105
#include <bits/stdc++.h>
using namespace std;
/* Define P as a shorthand for
the pair<int, pair<int,int>> type */
#define P pair <int, pair<int,int>>
class Solution {
public:
/* Function to find cheapest price from
src to dst with at most k stops */
int CheapestFlight(int n, vector<vector<int>>& flights,
int src, int dst, int k) {
// To store the graph
vector<pair<int,int>> adj[n];
// Adding edges to the graph
for(auto it : flights) {
adj[it[0]].push_back({it[1], it[2]});
}
// To store minimum distance
vector<int> minDist(n, 1e9);
/* Queue storing the elements of
the form {stops, {node, dist}} */
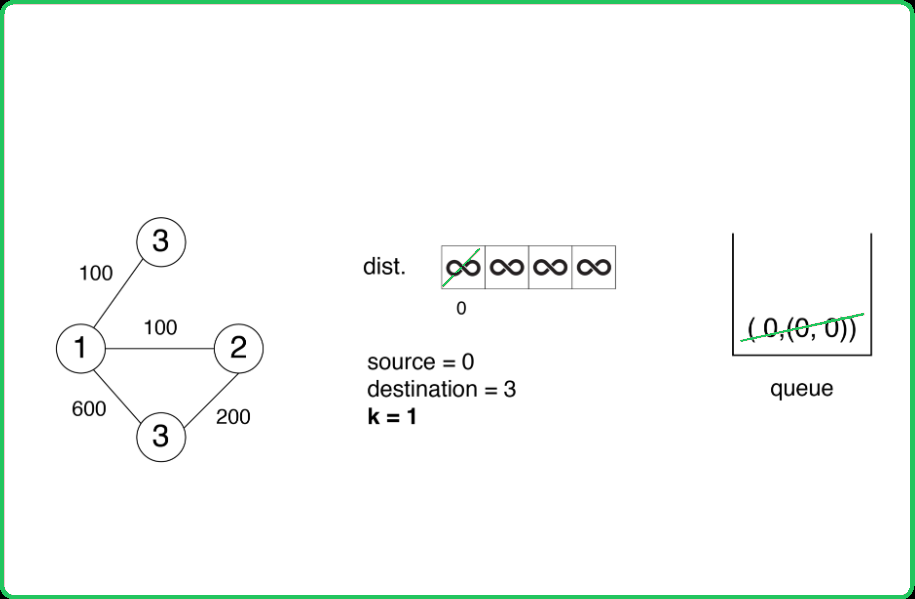
queue <P> q;
// Add the source to the queue
q.push({0, {src, 0}});
// Until the queue is empty
while(!q.empty()) {
// Get the element from queue
auto p = q.front(); q.pop();
int stops = p.first; //stops
int node = p.second.first; // node
int dist = p.second.second; // distance
/* If the number of stops taken exceed k,
skip and move to the next element */
if(stops > k) continue;
// Traverse all the neighbors
for(auto it : adj[node]) {
int adjNode = it.first; // Adjacent node
int edgeWt = it.second; // Edge weight
/* If the tentative distance to
reach adjacent node is smaller
than the known distance and number
of stops doesn't exceed k */
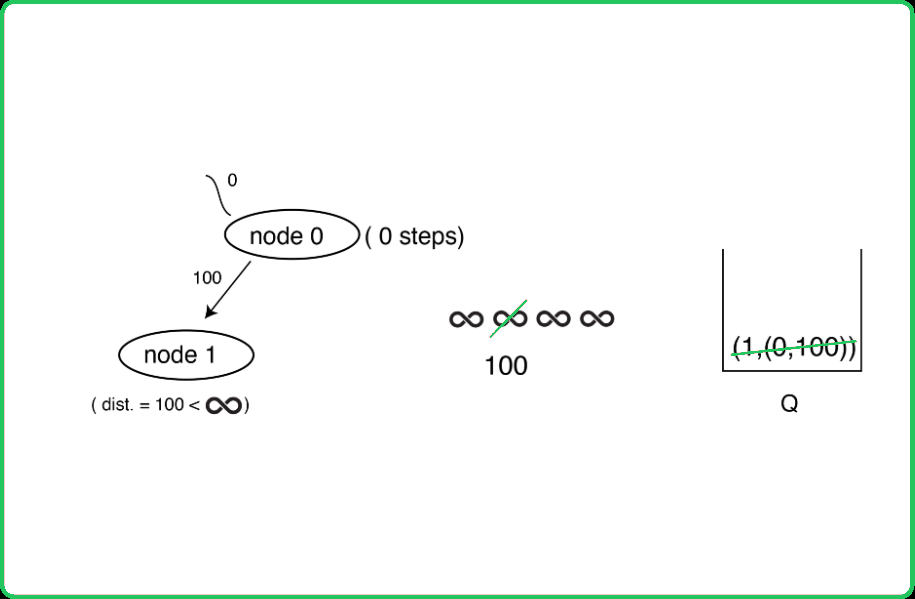
if(dist + edgeWt < minDist[adjNode] &&
stops <= k) {
// Update the known distance
minDist[adjNode] = dist + edgeWt;
// Add the new element to queue
q.push({stops+1, {adjNode, dist + edgeWt}});
}
}
}
/* If the destination is
unreachable, return -1 */
if(minDist[dst] == 1e9)
return -1;
// Otherwise return the result
return minDist[dst];
}
};
int main() {
int n = 4;
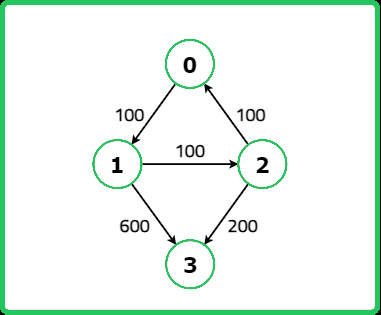
vector<vector<int>> flights = {
{0,1,100},
{1,2,100},
{2,0,100},
{1,3,600},
{2,3,200}
};
int src = 0, dst = 3, k = 1;
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to determine cheapest flight
from source to destination within K stops */
int ans =
sol.CheapestFLight(n, flights, src, dst, k);
// Output
cout << "The cheapest flight from source to destination within K stops is: " << ans;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798
import java.util.*;
class Solution {
/* Function to find the cheapest price
from src to dst with at most k stops */
public int CheapestFlight(int n, int[][] flights,
int src, int dst, int k) {
// To store the graph
List<List<int[]>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
// Adding edges to the graph
for (int[] flight : flights) {
adj.get(flight[0]).add(new int[]{flight[1], flight[2]});
}
// To store minimum distance
int[] minDist = new int[n];
Arrays.fill(minDist, Integer.MAX_VALUE);
/* Queue storing the elements of
the form {stops, {node, dist}} */
Queue<int[]> q = new LinkedList<>();
// Add the source to the queue
q.offer(new int[]{0, src, 0});
// Until the queue is empty
while (!q.isEmpty()) {
// Get the element from the queue
int[] p = q.poll();
int stops = p[0]; // stops
int node = p[1]; // node
int dist = p[2]; // distance
/* If the number of stops taken exceed k,
skip and move to the next element */
if (stops > k) continue;
// Traverse all the neighbors
for (int[] neighbor : adj.get(node)) {
int adjNode = neighbor[0]; // Adjacent node
int edgeWt = neighbor[1]; // Edge weight
/* If the tentative distance to
reach adjacent node is smaller
than the known distance and number
of stops doesn't exceed k */
if (dist + edgeWt < minDist[adjNode] &&
stops <= k) {
// Update the known distance
minDist[adjNode] = dist + edgeWt;
// Add the new element to the queue
q.offer(new int[]{stops + 1, adjNode, dist + edgeWt});
}
}
}
// If the destination is unreachable, return -1
if (minDist[dst] == Integer.MAX_VALUE)
return -1;
// Otherwise, return the result
return minDist[dst];
}
public static void main(String[] args) {
int n = 4;
int[][] flights = {
{0, 1, 100},
{1, 2, 100},
{2, 0, 100},
{1, 3, 600},
{2, 3, 200}
};
int src = 0, dst = 3, k = 1;
// Creating an instance of Solution class
Solution sol = new Solution();
// Function call to determine cheapest flight from source to destination within K stops
int ans = sol.CheapestFLight(n, flights, src, dst, k);
// Output
System.out.println("The cheapest flight from source to destination within K stops is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778
from collections import deque
from typing import List
class Solution:
# Function to find cheapest price from
# src to dst with at most k stops
def CheapestFlight(self, n: int, flights: List[List[int]],
src: int, dst: int, k: int) -> int:
# To store the graph
adj = [[] for _ in range(n)]
# Adding edges to the graph
for it in flights:
adj[it[0]].append((it[1], it[2]))
# To store minimum distance
minDist = [float('inf')] * n
# Queue storing the elements of
# the form {stops, {node, dist}}
q = deque([(0, src, 0)])
# Until the queue is empty
while q:
# Get the element from queue
stops, node, dist = q.popleft()
# If the number of stops taken exceed k,
# skip and move to the next element
if stops > k:
continue
# Traverse all the neighbors
for adjNode, edgeWt in adj[node]:
# If the tentative distance to reach adjacent
# node is smaller than the known distance
# and number of stops doesn't exceed k
if (dist + edgeWt < minDist[adjNode] and
stops <= k):
# Update the known distance
minDist[adjNode] = dist + edgeWt
# Add the new element to queue
q.append((stops + 1, adjNode, dist + edgeWt))
# If the destination is unreachable, return -1
if minDist[dst] == float('inf'):
return -1
# Otherwise return the result
return minDist[dst]
if __name__ == "__main__":
n = 4
flights = [
[0, 1, 100],
[1, 2, 100],
[2, 0, 100],
[1, 3, 600],
[2, 3, 200]
]
src, dst, k = 0, 3, 1
# Creating an instance of Solution class
sol = Solution()
# Function call to determine cheapest flight from source to destination within K stops
ans = sol.CheapestFLight(n, flights, src, dst, k)
# Output
print("The cheapest flight from source to destination within K stops is:", ans)
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182
class Solution {
/* Function to find the cheapest price
from src to dst with at most k stops */
CheapestFlight(n, flights, src, dst, k) {
// To store the graph
let adj = Array.from(
{ length: n },
() => []
);
// Adding edges to the graph
for (let flight of flights) {
adj[flight[0]].push([flight[1], flight[2]]);
}
// To store minimum distance
let minDist = new Array(n).fill(Infinity);
/* Queue storing the elements of
the form {stops, {node, dist}} */
let q = [[0, src, 0]];
// Until the queue is empty
while (q.length > 0) {
// Get the element from the queue
let [stops, node, dist] = q.shift();
/* If the number of stops taken exceed k,
skip and move to the next element */
if (stops > k) continue;
// Traverse all the neighbors
for (let [adjNode, edgeWt] of adj[node]) {
/* If the tentative distance to
reach adjacent node is smaller
than the known distance and number
of stops doesn't exceed k */
if (dist + edgeWt < minDist[adjNode] &&
stops <= k) {
// Update the known distance
minDist[adjNode] = dist + edgeWt;
// Add the new element to the queue
q.push([stops + 1, adjNode, dist + edgeWt]);
}
}
}
// If the destination is unreachable, return -1
if (minDist[dst] === Infinity)
return -1;
// Otherwise, return the result
return minDist[dst];
}
}
// Test case
const n = 4;
const flights = [
[0, 1, 100],
[1, 2, 100],
[2, 0, 100],
[1, 3, 600],
[2, 3, 200]
];
const src = 0, dst = 3, k = 1;
// Creating an instance of Solution class
const sol = new Solution();
// Function call to determine cheapest flight from source to destination within K stops
const ans = sol.CheapestFLight(n, flights, src, dst, k);
// Output
console.log("The cheapest flight from source to destination within K stops is:", ans);