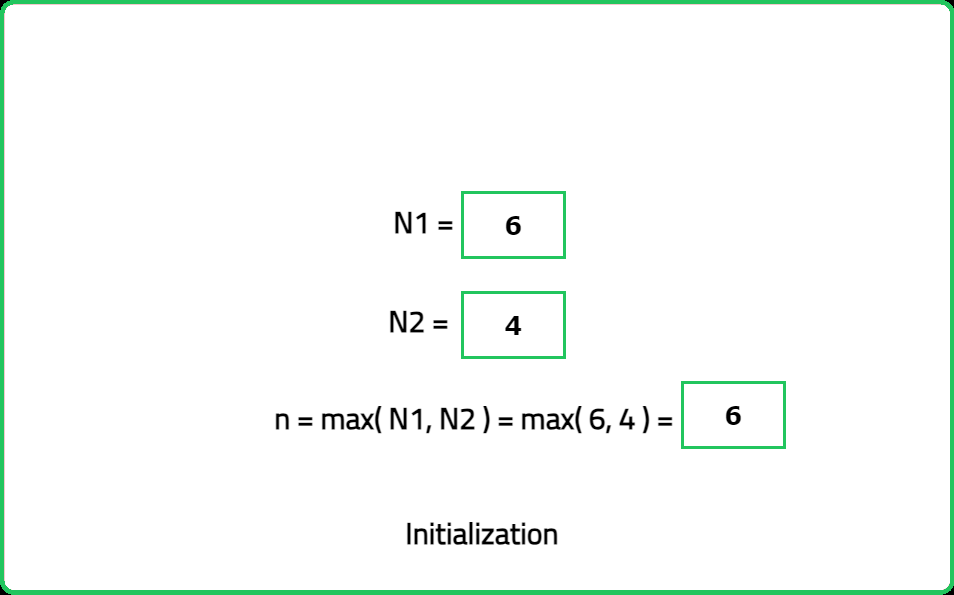
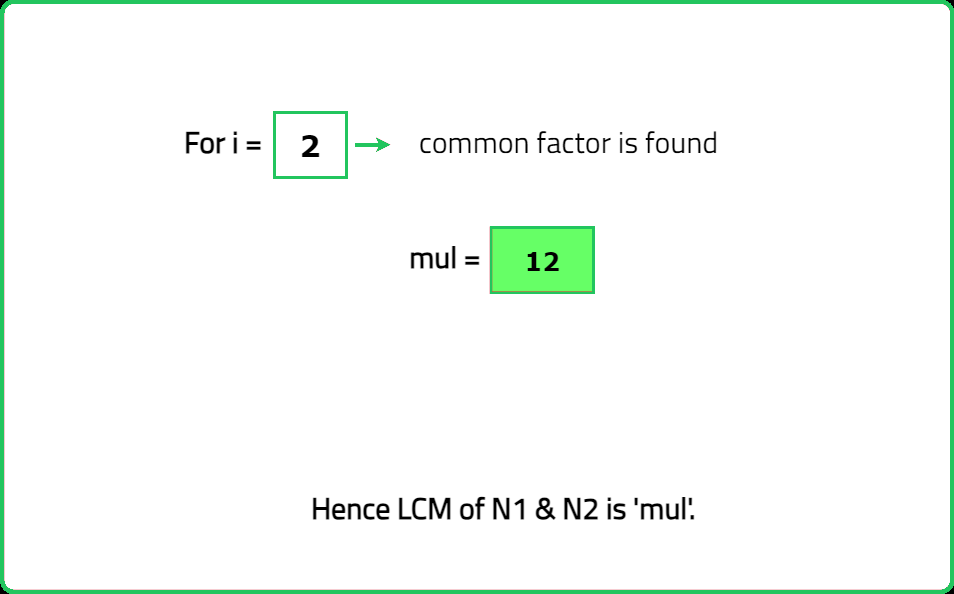
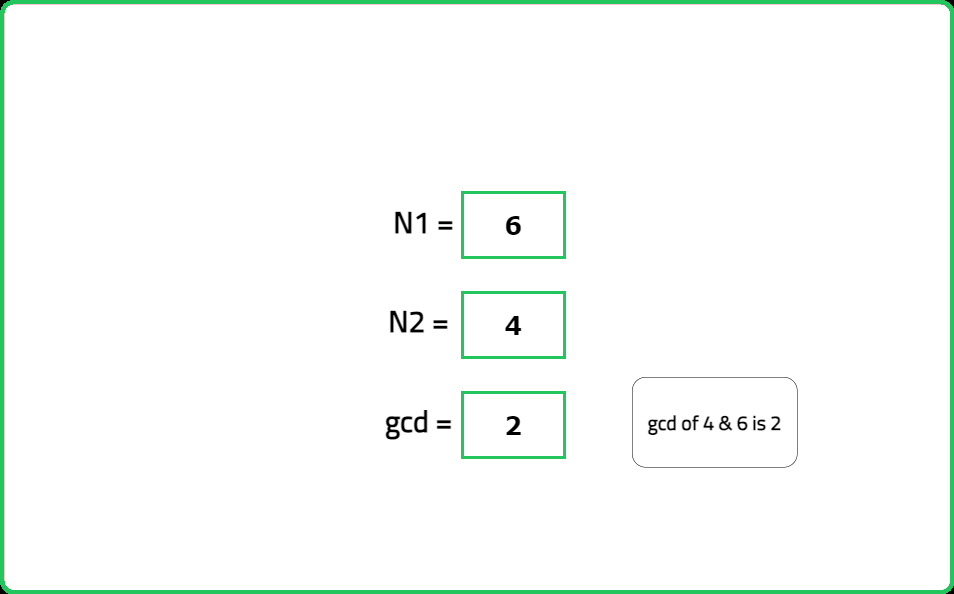
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to find the
GCD of two numbers*/
int GCD(int n1, int n2) {
/* Continue loop as long as both
n1 and n2 are greater than zero */
while(n1 > 0 && n2 > 0) {
/* If n1 is greater than n2, perform
modulo operation - n1 % n2 */
if(n1 > n2) {
n1 = n1 % n2;
}
/* Else perform modulo
operation - n2 % n1 */
else {
n2 = n2 % n1;
}
}
// If n1 is zero, GCD is stored in n2
if(n1 == 0) return n2;
//else GCD is stored in n1
return n1;
}
public:
// Function to find LCM of n1 and n2
int LCM(int n1,int n2) {
//Function call to find gcd
int gcd = GCD(n1, n2);
int lcm = (n1 * n2) / gcd;
// Return the LCM
return lcm;
}
};
int main()
{
int n1 = 3, n2 = 5;
/* Creating and instance of
Solution class */
Solution sol;
// Function call to get LCM of n1 and n2
int ans = sol.LCM(n1, n2);
cout << "The LCM of" << n1 << " and " << n2 << " is: " << ans;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
class Solution {
// Function to find the GCD of two numbers
private int GCD(int n1, int n2) {
/* Continue loop as long as both
n1 and n2 are greater than zero */
while (n1 > 0 && n2 > 0) {
/* If n1 is greater than n2, perform
modulo operation - n1 % n2 */
if (n1 > n2) {
n1 = n1 % n2;
}
/* Else perform modulo
operation - n2 % n1 */
else {
n2 = n2 % n1;
}
}
// If n1 is zero, GCD is stored in n2
if (n1 == 0) return n2;
// else GCD is stored in n1
return n1;
}
// Function to find LCM of n1 and n2
public int LCM(int n1, int n2) {
// Function call to find gcd
int gcd = GCD(n1, n2);
int lcm = (n1 * n2) / gcd;
// Return the LCM
return lcm;
}
public static void main(String[] args) {
int n1 = 3, n2 = 5;
/* Creating an instance of
Solution class */
Solution sol = new Solution();
// Function call to get LCM of n1 and n2
int ans = sol.LCM(n1, n2);
System.out.println("The LCM of " + n1 + " and " + n2 + " is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445
class Solution:
# Function to find the GCD of two numbers
def GCD(self, n1, n2):
# Continue loop as long as both
# n1 and n2 are greater than zero
while n1 > 0 and n2 > 0:
# If n1 is greater than n2, perform
# modulo operation - n1 % n2
if n1 > n2:
n1 = n1 % n2
# Else perform modulo
# operation - n2 % n1
else:
n2 = n2 % n1
# If n1 is zero, GCD is stored in n2
if n1 == 0:
return n2
# else GCD is stored in n1
return n1
# Function to find LCM of n1 and n2
def LCM(self, n1, n2):
# Function call to find gcd
gcd = self.GCD(n1, n2)
lcm = (n1 * n2) // gcd
# Return the LCM
return lcm
# Input numbers
n1, n2 = 3, 5
# Creating an instance of Solution class
sol = Solution()
# Function call to get LCM of n1 and n2
ans = sol.LCM(n1, n2)
print(f"The LCM of {n1} and {n2} is: {ans}")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
class Solution {
// Function to find the GCD of two numbers
GCD(n1, n2) {
/* Continue loop as long as both
n1 and n2 are greater than zero */
while (n1 > 0 && n2 > 0) {
/* If n1 is greater than n2, perform
modulo operation - n1 % n2 */
if (n1 > n2) {
n1 = n1 % n2;
}
/* Else perform modulo
operation - n2 % n1 */
else {
n2 = n2 % n1;
}
}
// If n1 is zero, GCD is stored in n2
if (n1 === 0) return n2;
// else GCD is stored in n1
return n1;
}
// Function to find LCM of n1 and n2
LCM(n1, n2) {
// Function call to find gcd
let gcd = this.GCD(n1, n2);
let lcm = (n1 * n2) / gcd;
// Return the LCM
return lcm;
}
}
// Input numbers
let n1 = 3, n2 = 5;
// Creating an instance of Solution class
let sol = new Solution();
// Function call to get LCM of n1 and n2
let ans = sol.LCM(n1, n2);
console.log(`The LCM of ${n1} and ${n2} is: ${ans}`);