Climbing stairs
Dynamic Programming
1D DP
Medium
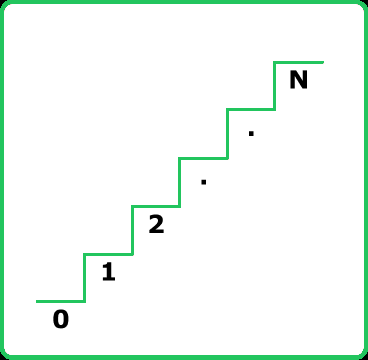
Given an integer n, there is a staircase with n steps, starting from the 0th step. Determine the number of unique ways to reach the nth step, given that each move can be either 1 or 2 steps at a time.
Examples:
Input: n = 2
Output: 2
Explanation: There are 2 unique ways to climb to the 2nd step:
1) 1 step + 1 step
2) 2 steps
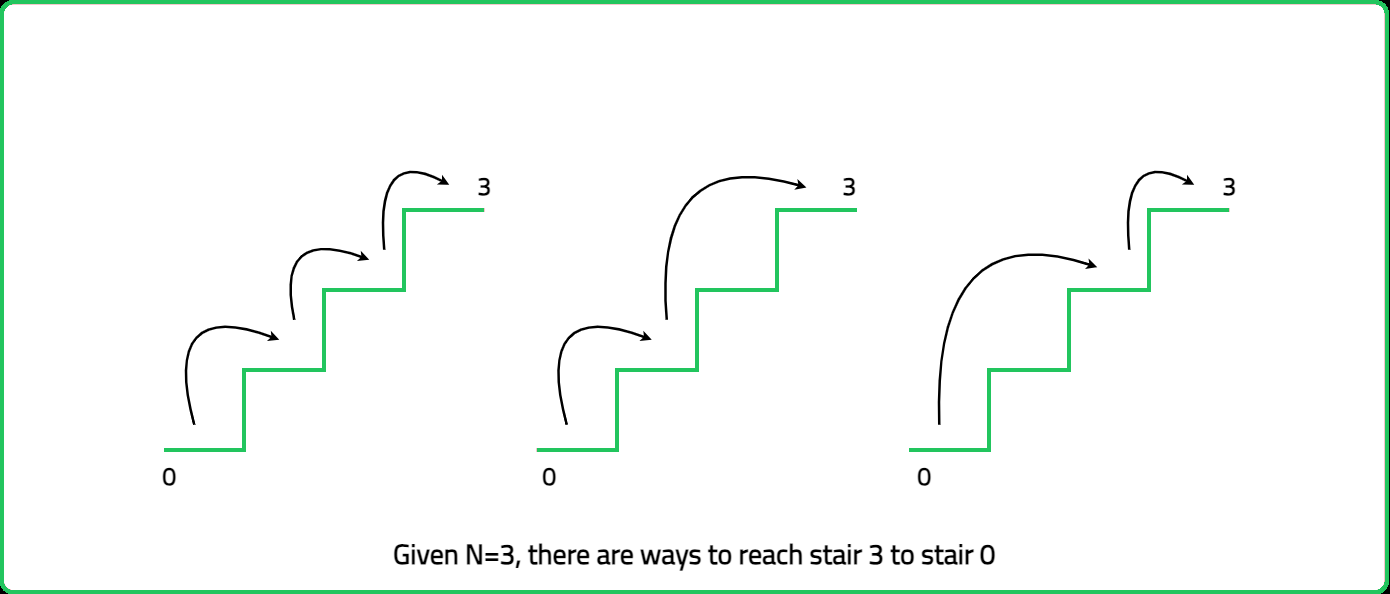
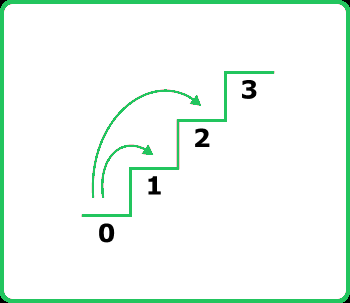
Input: n = 3
Output: 3
Explanation: There are 3 unique ways to climb to the 3rd step:
1) 1 step + 1 step + 1 step
2) 2 steps + 1 step
3) 1 step + 2 steps
Input: n = 1
Constraints
- 1 <= n <= 45
Hints
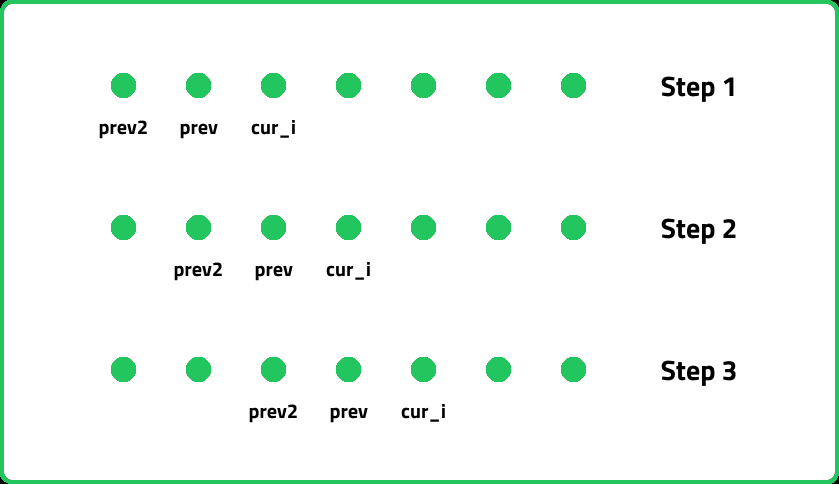
- To solve this problem, consider the last step before reaching n. You could have arrived at step n either from n-1 (by taking a 1-step move) or from n-2 (by taking a 2-step move). Thus, the number of ways to reach step n is the sum of the ways to reach n-1 and n-2.
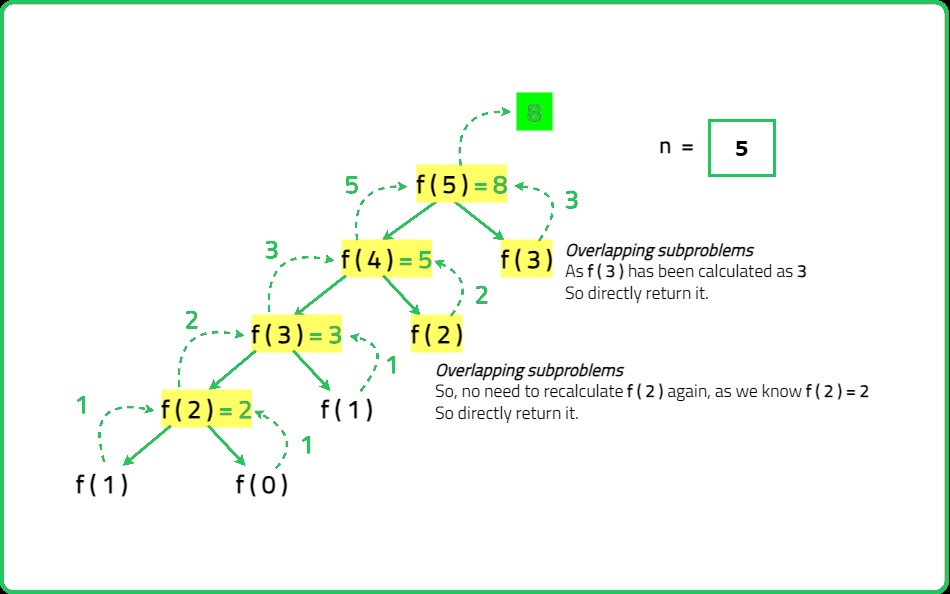
- A naive recursive approach results in exponential time complexity (O(2^n)) due to repeated computations. Instead, we can use memoization (top-down) or dynamic programming (bottom-up) to compute results efficiently in O(n) time and O(n) space.
Company Tags
Nutanix
Electronic Arts
Salesforce
Texas Instruments
Databricks
ARM
Etsy
GE Healthcare
Pinterest
Morgan Stanley
Broadcom
Twilio
Seagate Technology
Ernst & Young
Dropbox
Optum
Target
Shopify
KPMG
Micron Technology
Lyft
NVIDIA
Red Hat
Robinhood
Alibaba
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe