Target sum

The first approach that comes to our mind is to generate all subsequences and try both options of placing ‘-’ and ‘+’ signs and count the expression if it evaluates the answer.This surely will give us the answer but we can try something familiar to the concept we studied in the article Count Partitions with Given Difference

Understanding:

We can say that the given ‘target’ can be expressed as addition of two integers (say S1 and S2). S1 + S2 = target – (i)

Now, if the given array is [a,b,c,d,e], we want to place ‘+’ or ‘-’ signs in front of every array element and then add it. One example is :

+a-b-c+d+e which can be written as (+a+d+e) + (-b-c).

Therefore, we can say that S1=(+a+d+e) and S2=(-b-c) for this example.

If we calculate the total sum of elements of the array (say totSum), we can can say that, S1 = totSum - S2 – (ii)

Now solving for equations (i) and (ii), we can say that, S2 = (totSum - target)/2 – (iii)

Therefore this question is modified to “Count Number of subsets with sum (totSum - target)/2 ”. This is exactly what we had discussed in the article Count Subsets with Sum K.

There's some edge cases that need to be handled :

As the array elements are positive integers including zero, we don’t want to find the case when S2 is negative or we can say that totSum is lesser than D, therefore if totSum

From here on we will discuss the approach to “Count Subsets with Sum K” with the required modifications. Moreover, as the array elements can also contain 0, we will handle it as discussed above.

Steps to form the recursive solution:

Express the problem in terms of indexes:The array will have an index but there is one more parameter “target”. We are given the initial problem to find whether there exists in the whole array a subsequence whose sum is equal to the target.

So, initially, we need to find(n-1, target) which means that we are counting the number of subsequences in the array from index 0 to n-1, whose sum is equal to the target.

Try out all possible choices at a given index:As, all the subsequences need to be generated. We will use the pick/non-pick technique, we have two choices:

Exclude the current element from the subsequence: Try to find a subsequence without considering the current index element. For this, make a recursive call to f(ind-1,target).

Include the current element in the subsequence: Try to find a subsequence by considering the current index as element as part of subsequence. As arr[ind] is included, the updated target will be target - arr[ind]. Therefore, call f(ind-1,target-arr[ind]).

Note: Consider the current element in the subsequence only when the current element is less than or equal to the target.

f(ind, target){
    notTake = 0 + f(ind-1, target)
    take = 0
    if(arr[ind] <= target)
         take = f(ind-1, target-arr[ind])
}

Return sum of taken and notTaken:As we have to return the total count of subsets with the target sum, return the sum of 'taken' and 'notTaken' from our recursive call.

f(ind, target){
    notTake = 0 + f(ind-1, target)
    take = 0
    if(arr[ind] <= target)
         take = f(ind-1, target-arr[ind])
    return notTaken + taken
}

Base Cases:If target == 0, it means that we have already found the subsequence from the previous steps, so return 1. Also, if ind==0, it means we are at the first element, so return arr[ind]==target. If the element is equal to the target return 1 else return 0.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to count partitions of the 
    array into subsets with a given target sum*/
    int func(int ind, int target, vector<int>& arr) {
        // Base case
        if (ind == 0) {
            // Include or exclude the element
            if (target == 0 && arr[0] == 0)
                return 2; 
            //One way to partition
            if (target == 0 || target == arr[0])
                return 1; 
            return 0;
        }
        
        /* Calculate the number of ways
        without taking the current element*/
        int notTaken = func(ind - 1, target, arr);
    
        /* Calculate the number of ways
        by taking the current element*/
        int taken = 0;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr);
        
        // Return the sum of ways
        return (notTaken + taken);
    }
public:
    /* Function to count the number 
    of ways to achieve the target sum*/
    int targetSum(int n, int target, vector<int>& nums) {
        int totSum = 0;
        for (int i = 0; i < nums.size(); i++) {
            totSum += nums[i];
        }
    
        // Not possible to achieve the target sum
        if (totSum - target < 0)
            return 0; 
        /* The difference between the total 
        sum and target sum must be even*/
        if ((totSum - target) % 2 == 1)
            return 0; 
    
        // Calculate the required sum for each subset
        int s2 = (totSum - target) / 2; 
        
        //Return the result
        return func(n - 1, s2, nums); 
    }
};

int main() {
    vector<int> nums = {1, 2, 3, 1};
    int target = 3;
    int n = nums.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.targetSum(n, target, nums) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    /* Function to count partitions of the 
    array into subsets with a given target sum */
    private int func(int ind, int target, int[] arr) {
        // Base case
        if (ind == 0) {
            // Include or exclude the element
            if (target == 0 && arr[0] == 0)
                return 2; 
            // One way to partition
            if (target == 0 || target == arr[0])
                return 1; 
            return 0;
        }
        
        /* Calculate the number of ways
        without taking the current element */
        int notTaken = func(ind - 1, target, arr);
    
        /* Calculate the number of ways
        by taking the current element */
        int taken = 0;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr);
        
        // Return the sum of ways
        return (notTaken + taken);
    }

    /* Function to count the number 
    of ways to achieve the target sum */
    public int targetSum(int n, int target, int[] nums) {
        int totSum = 0;
        for (int i = 0; i < nums.length; i++) {
            totSum += nums[i];
        }
    
        // Not possible to achieve the target sum
        if (totSum - target < 0)
            return 0; 
        /* The difference between the total 
        sum and target sum must be even */
        if ((totSum - target) % 2 == 1)
            return 0; 
    
        // Calculate the required sum for each subset
        int s2 = (totSum - target) / 2; 
        
        // Return the result
        return func(n - 1, s2, nums); 
    }
    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 1};
        int target = 3;
        int n = nums.length; 
    
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.targetSum(n, target, nums));
    }
}
class Solution:
    """ Function to count partitions of the 
    array into subsets with a given target sum"""
    def func(self, ind, target, arr):
        # Base case
        if ind == 0:
            # Include or exclude the element
            if target == 0 and arr[0] == 0:
                return 2
            # One way to partition
            if target == 0 or target == arr[0]:
                return 1
            return 0
            
        """ Calculate the number of ways
        without taking the current element"""
        notTaken = self.func(ind - 1, target, arr)
        
        """ Calculate the number of ways 
        by taking the current element"""
        taken = 0
        if arr[ind] <= target:
            taken = self.func(ind - 1, target - arr[ind], arr)
        
        # Return the sum of ways
        return notTaken + taken

    """ Function to count the number of
    ways to achieve the target sum"""
    def targetSum(self, n, target, nums):
        totSum = sum(nums)
    
        # Not possible to achieve the target sum
        if totSum - target < 0:
            return 0
        """ The difference between the total
        sum and target sum must be even"""
        if (totSum - target) % 2 == 1:
            return 0
    
        # Calculate the required sum for each subset
        s2 = (totSum - target) // 2
    
        
        # Return the result
        return self.func(n - 1, s2, nums)

if __name__ == "__main__":
    nums = [1, 2, 3, 1]
    target = 3
    n = len(nums)
    
    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The total number of ways is", sol.targetSum(n, target, nums))
class Solution {
    /* Function to count partitions of the 
    array into subsets with a given target sum */
    func(ind, target, arr) {
        // Base case
        if (ind === 0) {
            // Include or exclude the element
            if (target === 0 && arr[0] === 0)
                return 2;
            // One way to partition
            if (target === 0 || target === arr[0])
                return 1;
            return 0;
        }
        
        /* Calculate the number of ways 
        without taking the current element*/
        const notTaken = this.func(ind - 1, target, arr);
    
        /* Calculate the number of ways
        by taking the current element*/
        let taken = 0;
        if (arr[ind] <= target)
            taken = this.func(ind - 1, target - arr[ind], arr);
        
        // Return the sum of ways 
        return notTaken + taken;
    }

    /* Function to count the number of 
    ways to achieve the target sum */
    targetSum(n, target, nums) {
        const totSum = nums.reduce((acc, num) => acc + num, 0);
    
        // Not possible to achieve the target sum
        if (totSum - target < 0)
            return 0;
        /* The difference between the total
        sum and target sum must be even*/
        if ((totSum - target) % 2 === 1)
            return 0;
    
        // Calculate the required sum for each subset
        const s2 = (totSum - target) / 2;
        
        // Return the result
        return this.func(n - 1, s2, nums);
    }
}

const nums = [1, 2, 3, 1];
const target = 3;
const n = nums.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.targetSum(n, target, nums));

Complexity Analysis:

Time Complexity:O(2^N), As each index has 2 choices and there are total of N elements.

Space Complexity:O(N), As we are using recursive stack space of O(N).

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

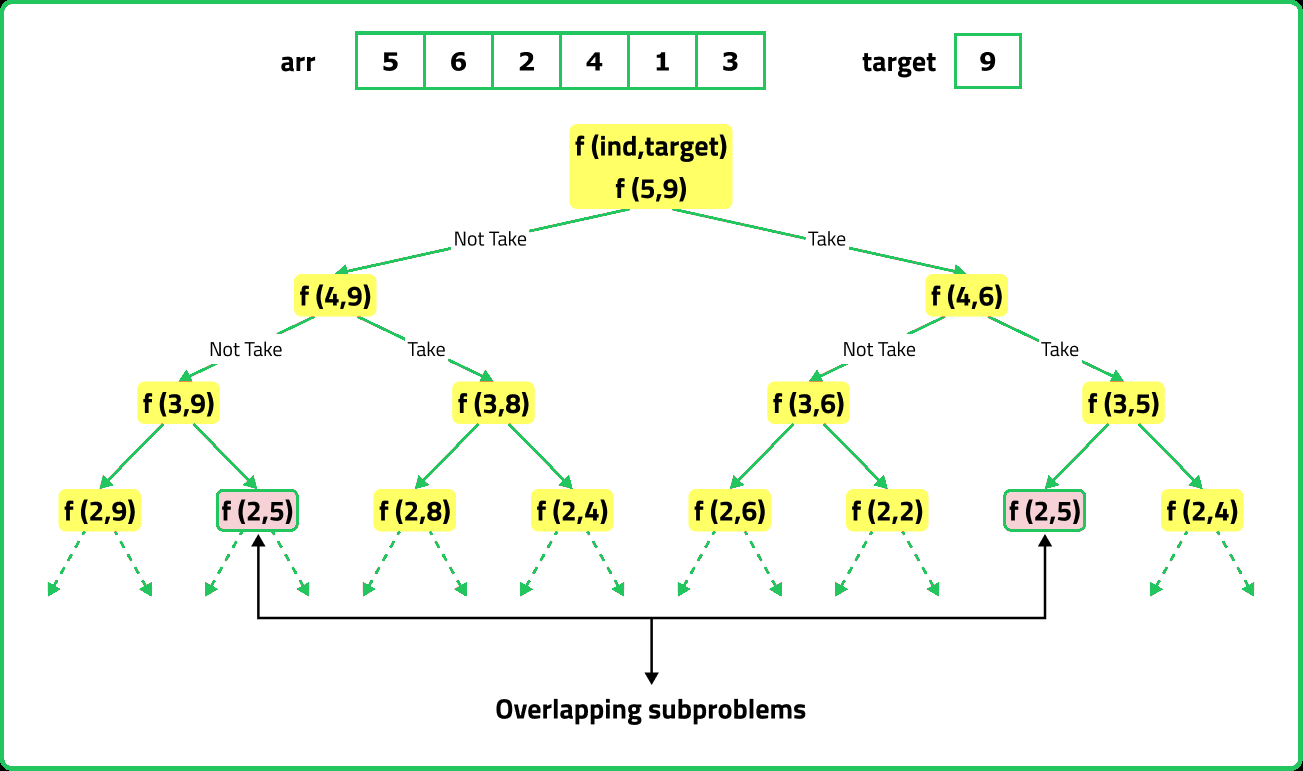
In order to convert a recursive solution to memoization the following steps will be taken:

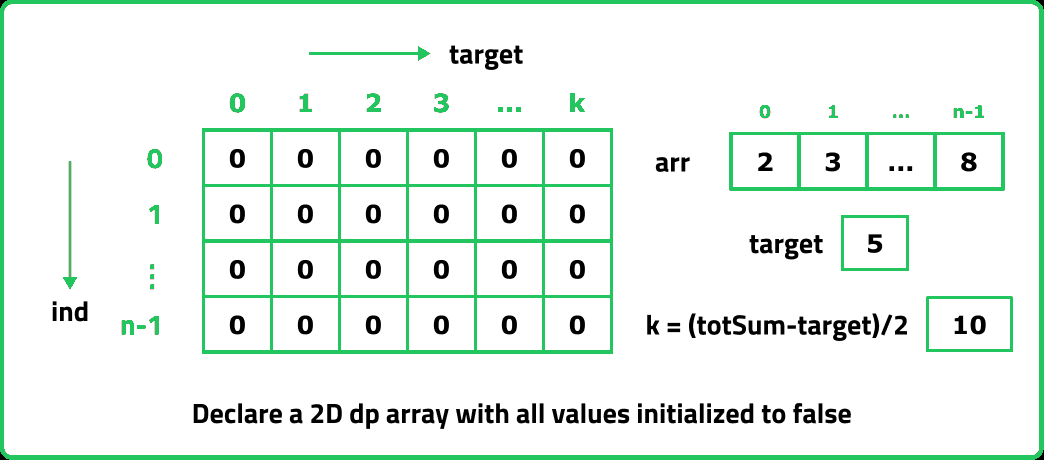
Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'target' only values between 0 to target. Therefore, we need 2D dp array.

The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to count partitions of the 
    array into subsets with a given target sum*/
    int func(int ind, int target, vector<int>& arr, vector<vector<int>>& dp) {
        // Base case
        if (ind == 0) {
            // Include or exclude the element
            if (target == 0 && arr[0] == 0)
                return 2; 
            //One way to partition
            if (target == 0 || target == arr[0])
                return 1; 
            return 0;
        }
    
        /* If the result for this index and target
        sum is already calculated, return it*/
        if (dp[ind][target] != -1)
            return dp[ind][target];
        
        /* Calculate the number of ways
        without taking the current element*/
        int notTaken = func(ind - 1, target, arr, dp);
    
        /* Calculate the number of ways
        by taking the current element*/
        int taken = 0;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr, dp);
        
        /* Store the sum of ways in
        the DP array and return it*/
        return dp[ind][target] = (notTaken + taken);
    }
public:
    /* Function to count the number 
    of ways to achieve the target sum*/
    int targetSum(int n, int target, vector<int>& nums) {
        int totSum = 0;
        for (int i = 0; i < nums.size(); i++) {
            totSum += nums[i];
        }
    
        // Not possible to achieve the target sum
        if (totSum - target < 0)
            return 0; 
        /* The difference between the total 
        sum and target sum must be even*/
        if ((totSum - target) % 2 == 1)
            return 0; 
    
        // Calculate the required sum for each subset
        int s2 = (totSum - target) / 2; 
    
        // Initialize DP table
        vector<vector<int>> dp(n, vector<int>(s2 + 1, -1)); 
        
        //Return the result
        return func(n - 1, s2, nums, dp); 
    }
};

int main() {
    vector<int> nums = {1, 2, 3, 1};
    int target = 3;
    int n = nums.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.targetSum(n, target, nums) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    /* Function to count partitions of the 
    array into subsets with a given target sum */
    private int func(int ind, int target, int[] arr, int[][] dp) {
        // Base case
        if (ind == 0) {
            // Include or exclude the element
            if (target == 0 && arr[0] == 0)
                return 2; 
            // One way to partition
            if (target == 0 || target == arr[0])
                return 1; 
            return 0;
        }
    
        /* If the result for this index and target
        sum is already calculated, return it */
        if (dp[ind][target] != -1)
            return dp[ind][target];
        
        /* Calculate the number of ways
        without taking the current element */
        int notTaken = func(ind - 1, target, arr, dp);
    
        /* Calculate the number of ways
        by taking the current element */
        int taken = 0;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr, dp);
        
        /* Store the sum of ways in
        the DP array and return it */
        return dp[ind][target] = (notTaken + taken);
    }

    /* Function to count the number 
    of ways to achieve the target sum */
    public int targetSum(int n, int target, int[] nums) {
        int totSum = 0;
        for (int i = 0; i < nums.length; i++) {
            totSum += nums[i];
        }
    
        // Not possible to achieve the target sum
        if (totSum - target < 0)
            return 0; 
        /* The difference between the total 
        sum and target sum must be even */
        if ((totSum - target) % 2 == 1)
            return 0; 
    
        // Calculate the required sum for each subset
        int s2 = (totSum - target) / 2; 
    
        // Initialize DP table
        int[][] dp = new int[n][s2 + 1];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }
        
        // Return the result
        return func(n - 1, s2, nums, dp); 
    }
}

public class Main {
    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 1};
        int target = 3;
        int n = nums.length; 
    
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.targetSum(n, target, nums));
    }
}
class Solution:
    """ Function to count partitions of the 
    array into subsets with a given target sum"""
    def func(self, ind, target, arr, dp):
        # Base case
        if ind == 0:
            # Include or exclude the element
            if target == 0 and arr[0] == 0:
                return 2
            # One way to partition
            if target == 0 or target == arr[0]:
                return 1
            return 0
        
        """ If the result for this index and target 
        sum is already calculated, return it"""
        if dp[ind][target] != -1:
            return dp[ind][target]
        
        """ Calculate the number of ways
        without taking the current element"""
        notTaken = self.func(ind - 1, target, arr, dp)
        
        """ Calculate the number of ways 
        by taking the current element"""
        taken = 0
        if arr[ind] <= target:
            taken = self.func(ind - 1, target - arr[ind], arr, dp)
        
        """ Store the sum of ways in 
        the DP array and return it"""
        dp[ind][target] = notTaken + taken
        return dp[ind][target]

    """ Function to count the number of
    ways to achieve the target sum"""
    def targetSum(self, n, target, nums):
        totSum = sum(nums)
    
        # Not possible to achieve the target sum
        if totSum - target < 0:
            return 0
        """ The difference between the total
        sum and target sum must be even"""
        if (totSum - target) % 2 == 1:
            return 0
    
        # Calculate the required sum for each subset
        s2 = (totSum - target) // 2
    
        # Initialize DP table
        dp = [[-1] * (s2 + 1) for _ in range(n)]
        
        # Return the result
        return self.func(n - 1, s2, nums, dp)

if __name__ == "__main__":
    nums = [1, 2, 3, 1]
    target = 3
    n = len(nums)
    
    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The total number of ways is", sol.targetSum(n, target, nums))
class Solution {
    /* Function to count partitions of the 
    array into subsets with a given target sum */
    func(ind, target, arr, dp) {
        // Base case
        if (ind === 0) {
            // Include or exclude the element
            if (target === 0 && arr[0] === 0)
                return 2;
            // One way to partition
            if (target === 0 || target === arr[0])
                return 1;
            return 0;
        }
    
        /* If the result for this index and target
        sum is already calculated, return it*/
        if (dp[ind][target] !== -1)
            return dp[ind][target];
        
        /* Calculate the number of ways 
        without taking the current element*/
        const notTaken = this.func(ind - 1, target, arr, dp);
    
        /* Calculate the number of ways 
        by taking the current element*/
        let taken = 0;
        if (arr[ind] <= target)
            taken = this.func(ind - 1, target - arr[ind], arr, dp);
        
        /* Store the sum of ways in
        the DP array and return it*/
        dp[ind][target] = notTaken + taken;
        return dp[ind][target];
    }

    /* Function to count the number of
    ways to achieve the target sum */
    targetSum(n, target, nums) {
        const totSum = nums.reduce((acc, num) => acc + num, 0);
    
        // Not possible to achieve the target sum
        if (totSum - target < 0)
            return 0;
        /* The difference between the total
        sum and target sum must be even*/
        if ((totSum - target) % 2 === 1)
            return 0;
    
        // Calculate the required sum for each subset
        const s2 = (totSum - target) / 2;
    
        // Initialize DP table
        const dp = Array.from({ length: n }, () => Array(s2 + 1).fill(-1));
        
        // Return the result
        return this.func(n - 1, s2, nums, dp);
    }
}
const nums = [1, 2, 3, 1];
const target = 3;
const n = nums.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.targetSum(n, target, nums));

Complexity Analysis:

Time Complexity: O(N*target), There are 'N*target' states therefore at max ‘N*target’ new problems will be solved.

Space Complexity:O(N*target) + O(N), As we are using a recursion stack space(O(N)) and a 2D array ( O(N*target)).

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

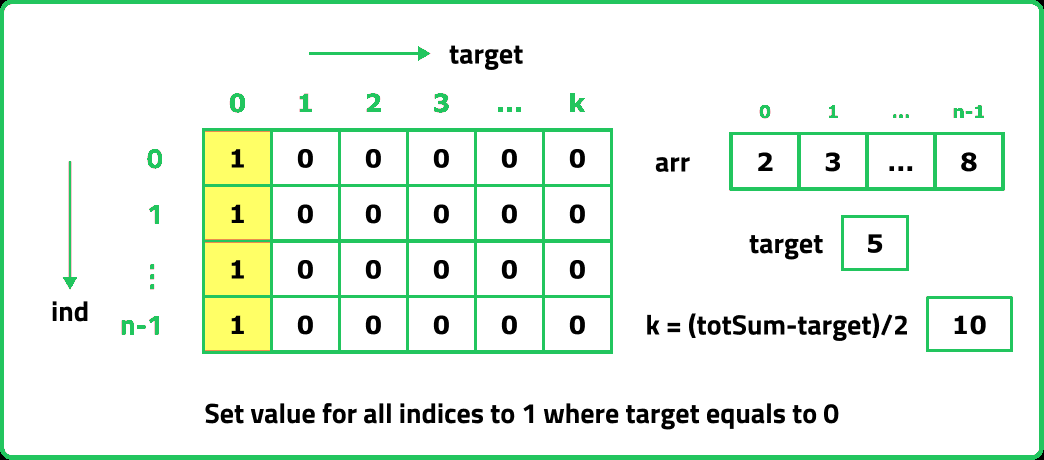
Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n) and including 0 its n, where n is the size of array, for 'target' can have any values between 0 to 'target'. So we need a 2D dp array. Set its type as int and initialize it as 0.

Setting Base Cases in the Array: In the recursive code, our base condition was when target == 0, it means the required subset is found and we were returning 1. So, set '1' in the dp array for every index where target = 0.

The first row dp[0][] indicates that only the first element of the array is considered, therefore for the target value equal to arr[0], only cell with that target will be true, so explicitly set dp[0][arr[0]] =1, (dp[0][arr[0]] means that we are considering the first element of the array with the target equal to the first element itself). Please note that it can happen that arr[0]>target, so we first check it: if(arr[0]<=target) then set dp[0][arr[0]] = 1

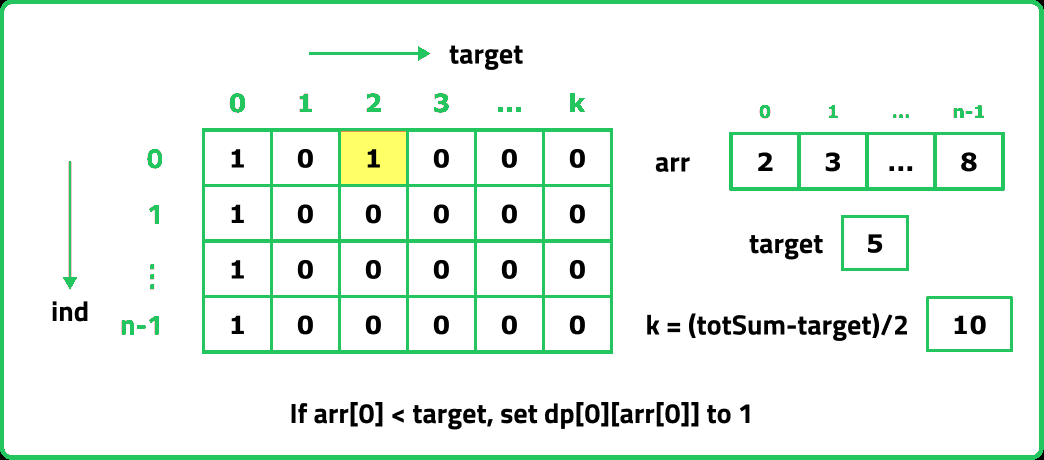
Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.

Returning the answer: At last dp[n-1][target] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.

If we observe the relation obtained in tabulation approach, dp[ind][target] = dp[ind-1][target] + dp[ind-1][target-arr[ind]], we see that to calculate a value of a cell of the dp array, only the previous row values (say prev) are needed. So, we don’t need to store an entire array. Hence, we can space optimize it.

#include <bits/stdc++.h>
using namespace std;

class Solution{
    const int mod = (int)1e9 + 7;
private:
    /* Function to count partitions of the 
    array into subsets with a given target sum*/
    int func(vector<int>& arr, int target) {
        int n = arr.size();

        vector<vector<int>> dp(n, vector<int>(target + 1, 0));

        if (arr[0] == 0) 
            // 2 cases - pick and not pick
            dp[0][0] = 2;   
        else
            // 1 case - not pick
            dp[0][0] = 1;  

        if (arr[0] != 0 && arr[0] <= target)
            // 1 case - pick
            dp[0][arr[0]] = 1;  

        for (int ind = 1; ind < n; ind++) {
            for (int tar = 0; tar <= target; tar++) {

                int notTaken = dp[ind - 1][tar];

                int taken = 0;
                if (arr[ind] <= tar)
                    taken = dp[ind - 1][tar - arr[ind]];

                dp[ind][tar] = (notTaken + taken) % mod;
            }
        }
        return dp[n - 1][target];
    }
public:
    /* Function to count the number 
    of ways to achieve the target sum*/
    int targetSum(int n, int target, vector<int>& nums) {
        int totSum = 0;
        for (int i = 0; i < n; i++) {
            totSum += nums[i];
        }

        // Checking for edge cases
        if (totSum - target < 0 || (totSum - target) % 2 != 0)
            // Not possible to achieve target sum
            return 0;  

        return func(nums, (totSum - target) / 2);
    }
};

int main() {
    vector<int> nums = {1, 2, 3, 1};
    int target = 3;
    int n = nums.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.targetSum(n, target, nums) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    private static final int MOD = (int)1e9 + 7;

    /* Function to count partitions of the 
    array into subsets with a given target sum */
    private int func(int[] arr, int target) {
        int n = arr.length;
        int[][] dp = new int[n][target + 1];

        if (arr[0] == 0) 
            // 2 cases - pick and not pick
            dp[0][0] = 2;   
        else
            // 1 case - not pick
            dp[0][0] = 1;  

        if (arr[0] != 0 && arr[0] <= target)
            // 1 case - pick
            dp[0][arr[0]] = 1;  

        for (int ind = 1; ind < n; ind++) {
            for (int tar = 0; tar <= target; tar++) {
                int notTaken = dp[ind - 1][tar];

                int taken = 0;
                if (arr[ind] <= tar)
                    taken = dp[ind - 1][tar - arr[ind]];

                dp[ind][tar] = (notTaken + taken) % MOD;
            }
        }
        return dp[n - 1][target];
    }

    /* Function to count the number 
    of ways to achieve the target sum */
    public int targetSum(int n, int target, int[] nums) {
        int totSum = 0;
        for (int num : nums) {
            totSum += num;
        }

        // Checking for edge cases
        if (totSum - target < 0 || (totSum - target) % 2 != 0)
            // Not possible to achieve target sum
            return 0;  

        return func(nums, (totSum - target) / 2);
    }
}

public class Main {
    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 1};
        int target = 3;
        int n = nums.length; 
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.targetSum(n, target, nums));
    }
}
MOD = int(1e9 + 7)

class Solution:
    """ Function to count partitions of the 
    array into subsets with a given target sum"""
    def func(self, arr, target):
        n = len(arr)
        dp = [[0] * (target + 1) for _ in range(n)]

        if arr[0] == 0:
            # 2 cases - pick and not pick
            dp[0][0] = 2
        else:
            # 1 case - not pick
            dp[0][0] = 1

        if arr[0] != 0 and arr[0] <= target:
            # 1 case - pick
            dp[0][arr[0]] = 1

        for ind in range(1, n):
            for tar in range(target + 1):
                notTaken = dp[ind - 1][tar]

                taken = 0
                if arr[ind] <= tar:
                    taken = dp[ind - 1][tar - arr[ind]]

                dp[ind][tar] = (notTaken + taken) % MOD
        return dp[n - 1][target]

    """ Function to count the number of 
    ways to achieve the target sum"""
    def targetSum(self, n, target, nums):
        totSum = sum(nums)

        # Checking for edge cases
        if totSum - target < 0 or (totSum - target) % 2 != 0:
            # Not possible to achieve target sum
            return 0

        return self.func(nums, (totSum - target) // 2)

if __name__ == "__main__":
    nums = [1, 2, 3, 1]
    target = 3
    n = len(nums)
    
    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The total number of ways is", sol.targetSum(n, target, nums))
const MOD = 1e9 + 7;

class Solution {
    /* Function to count partitions of the 
    array into subsets with a given target sum */
    func(arr, target) {
        const n = arr.length;
        const dp = Array.from({ length: n }, () => Array(target + 1).fill(0));

        if (arr[0] === 0) 
            // 2 cases - pick and not pick
            dp[0][0] = 2;   
        else
            // 1 case - not pick
            dp[0][0] = 1;  

        if (arr[0] !== 0 && arr[0] <= target)
            // 1 case - pick
            dp[0][arr[0]] = 1;  

        for (let ind = 1; ind < n; ind++) {
            for (let tar = 0; tar <= target; tar++) {
                const notTaken = dp[ind - 1][tar];

                let taken = 0;
                if (arr[ind] <= tar)
                    taken = dp[ind - 1][tar - arr[ind]];

                dp[ind][tar] = (notTaken + taken) % MOD;
            }
        }
        return dp[n - 1][target];
    }

    /* Function to count the number 
    of ways to achieve the target sum */
    targetSum(n, target, nums) {
        const totSum = nums.reduce((acc, num) => acc + num, 0);

        // Checking for edge cases
        if (totSum - target < 0 || (totSum - target) % 2 !== 0)
            // Not possible to achieve target sum
            return 0;  

        return this.func(nums, (totSum - target) / 2);
    }
}

const nums = [1, 2, 3, 1];
const target = 3;
const n = nums.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.targetSum(n, target, nums));

Complexity Analysis:

Time Complexity: O(N*target), As, here are three nested loops that account for O(N*target) complexity.

Space Complexity:O(N*target), As a 2D array of size N*target is used.

Steps to consider for space optimization:

Declare an array to store results of subproblems for the previous element as 'prev'. Initialize the 'prev' array for the first element of the array, as we did in tabulation to handle base cases.
Now, intitialize nested loops for 'ind' and 'target' and declare an array 'cur' to store the calculations of current row. Fill the 'cur' array using same logic discussed in the tabulation approach, lastly assign the 'cur' array to 'prev' for the next iteration.
After the calculations end return prev[target] as an answer.

#include <bits/stdc++.h>
using namespace std;

class Solution{
    const int mod = (int)1e9 + 7;
private:
    /* Function to count partitions of the 
    array into subsets with a given target sum*/
    int func(vector<int>& num, int target) {
        int n = num.size();

        vector<int> prev(target + 1, 0);

        if (num[0] == 0)
            // 2 cases - pick and not pick
            prev[0] = 2;  
        else
            // 1 case - not pick
            prev[0] = 1;  

        if (num[0] != 0 && num[0] <= target)
            // 1 case - pick
            prev[num[0]] = 1;  

        for (int ind = 1; ind < n; ind++) {
            
            // Initialize current DP state
            vector<int> cur(target + 1, 0);
            for (int tar = 0; tar <= target; tar++) {
                /* Number of ways without 
                taking the current element*/
                int notTaken = prev[tar];

                int taken = 0;
                if (num[ind] <= tar)
                    // Number of ways by taking current element
                    taken = prev[tar - num[ind]];
                
                // Total number of ways for current sum
                cur[tar] = (notTaken + taken) % mod;
            }
            /* Update previous DP state
            for the next iteration*/
            prev = cur;
        }
        // Return the number of ways
        return prev[target];
    }
public:
    /* Function to count the number 
    of ways to achieve the target sum*/
    int targetSum(int n, int target, vector<int>& nums) {
        int totSum = 0;
        for (int i = 0; i < n; i++) {
            totSum += nums[i];
        }

        // Checking for edge cases
        if (totSum - target < 0 || (totSum - target) % 2 != 0)
            // Not possible to achieve target sum
            return 0;  

        return func(nums, (totSum - target) / 2);
    }
};

int main() {
    vector<int> nums = {1, 2, 3, 1};
    int target = 3;
    int n = nums.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.targetSum(n, target, nums) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    final int mod = (int)1e9 + 7;

    /* Function to count partitions of the array
    into subsets with a given target sum*/
    private int func(int[] num, int target) {
        int n = num.length;

        int[] prev = new int[target + 1];
        
        if (num[0] == 0)
            // 2 cases - pick and not pick
            prev[0] = 2;
        else
            // 1 case - not pick
            prev[0] = 1;

        if (num[0] != 0 && num[0] <= target)
            // 1 case - pick
            prev[num[0]] = 1;

        for (int ind = 1; ind < n; ind++) {
            int[] cur = new int[target + 1];
            for (int tar = 0; tar <= target; tar++) {
                // Number of ways without taking current element
                int notTaken = prev[tar];

                int taken = 0;
                if (num[ind] <= tar)
                    // Number of ways by taking current element
                    taken = prev[tar - num[ind]];

                // Total number of ways for current sum
                cur[tar] = (notTaken + taken) % mod;
            }
            // Update DP state for next iteration
            prev = cur;
        }
        // Return the number of ways
        return prev[target];
    }

    /* Function to count the number of 
    ways to achieve the target sum*/
    public int targetSum(int n, int target, int[] nums) {
        int totSum = 0;
        for (int i = 0; i < n; i++) {
            totSum += nums[i];
        }

        // Checking for edge cases
        if (totSum - target < 0 || (totSum - target) % 2 != 0)
            // Not possible to achieve target sum
            return 0;

        return func(nums, (totSum - target) / 2);
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 1};
        int target = 3;
        int n = nums.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.targetSum(n, target, nums));
    }
}
class Solution:
    mod = int(1e9 + 7)
    
    """ Function to count partitions of the 
    array into subsets with a given target sum"""
    def func(self, num, target):
        n = len(num)
        prev = [0] * (target + 1)

        if num[0] == 0:
            # 2 cases - pick and not pick
            prev[0] = 2
        else:
            # 1 case - not pick
            prev[0] = 1

        if num[0] != 0 and num[0] <= target:
            # 1 case - pick
            prev[num[0]] = 1

        for ind in range(1, n):
            cur = [0] * (target + 1)
            for tar in range(target + 1):
                # Number of ways without taking the current element
                notTaken = prev[tar]

                taken = 0
                if num[ind] <= tar:
                    # Number of ways by taking current element
                    taken = prev[tar - num[ind]]

                # Total number of ways for current sum
                cur[tar] = (notTaken + taken) % self.mod
            
            # Update previous DP state for the next iteration
            prev = cur

        # Return the number of ways
        return prev[target]
    
    
    """ Function to count the number of
    ways to achieve the target sum"""
    def targetSum(self, n, target, nums):
        totSum = sum(nums)

        # Checking for edge cases
        if totSum - target < 0 or (totSum - target) % 2 != 0:
            # Not possible to achieve target sum
            return 0

        return self.func(nums, (totSum - target) // 2)

nums = [1, 2, 3, 1]
target = 3
n = len(nums)

# Create an instance of Solution class
sol = Solution()

# Print the result
print("The total number of ways is", sol.targetSum(n, target, nums))
const MOD = 1e9 + 7;

class Solution {
    /* Function to count partitions of the 
    array into subsets with a given target sum */
    func(num, target) {
        let n = num.length;
        let prev = new Array(target + 1).fill(0);

        if (num[0] === 0) {
            // 2 cases - pick and not pick
            prev[0] = 2;
        } else {
            // 1 case - not pick
            prev[0] = 1;
        }

        if (num[0] !== 0 && num[0] <= target) {
            // 1 case - pick
            prev[num[0]] = 1;
        }

        for (let ind = 1; ind < n; ind++) {
            let cur = new Array(target + 1).fill(0);
            for (let tar = 0; tar <= target; tar++) {
                // Number of ways without taking current element
                let notTaken = prev[tar];

                let taken = 0;
                if (num[ind] <= tar) {
                    // Number of ways by taking current element
                    taken = prev[tar - num[ind]];
                }

                // Total number of ways for current sum
                cur[tar] = (notTaken + taken) % MOD;
            }
            // Update previous DP state for the next iteration
            prev = cur;
        }
        return prev[target];
    }

    /* Function to count the number 
    of ways to achieve the target sum */
    targetSum(n, target, nums) {
        const totSum = nums.reduce((acc, num) => acc + num, 0);

        // Checking for edge cases
        if (totSum - target < 0 || (totSum - target) % 2 !== 0) {
            // Not possible to achieve target sum
            return 0;  
        }

        return this.func(nums, (totSum - target) / 2);
    }
}

const nums = [1, 2, 3, 1];
const target = 3;
const n = nums.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.targetSum(n, target, nums));

Complexity Analysis:

Time Complexity:O(N*Target), as there are N*Target states therefore at max ‘N*Target’ new problems will be solved.

Space Complexity:O(Target), as a 2D array of size (Target+1) is used.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Understanding:

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Steps to consider for space optimization:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code

Facts