LRU Cache
- The concept of a Least Recently Used (LRU) cache is widely used in operating systems, databases, and software applications
- For instance, in a web browser, it's used to cache web pages
- It holds the most recently accessed pages for a quick revisit, discarding the least recently viewed pages when the cache limit is exceeded
- The LRU cache data structure, as highlighted in this problem, allows the system to maintain and manage such resources efficiently in O(1) time, improving the overall performance of the software application or system
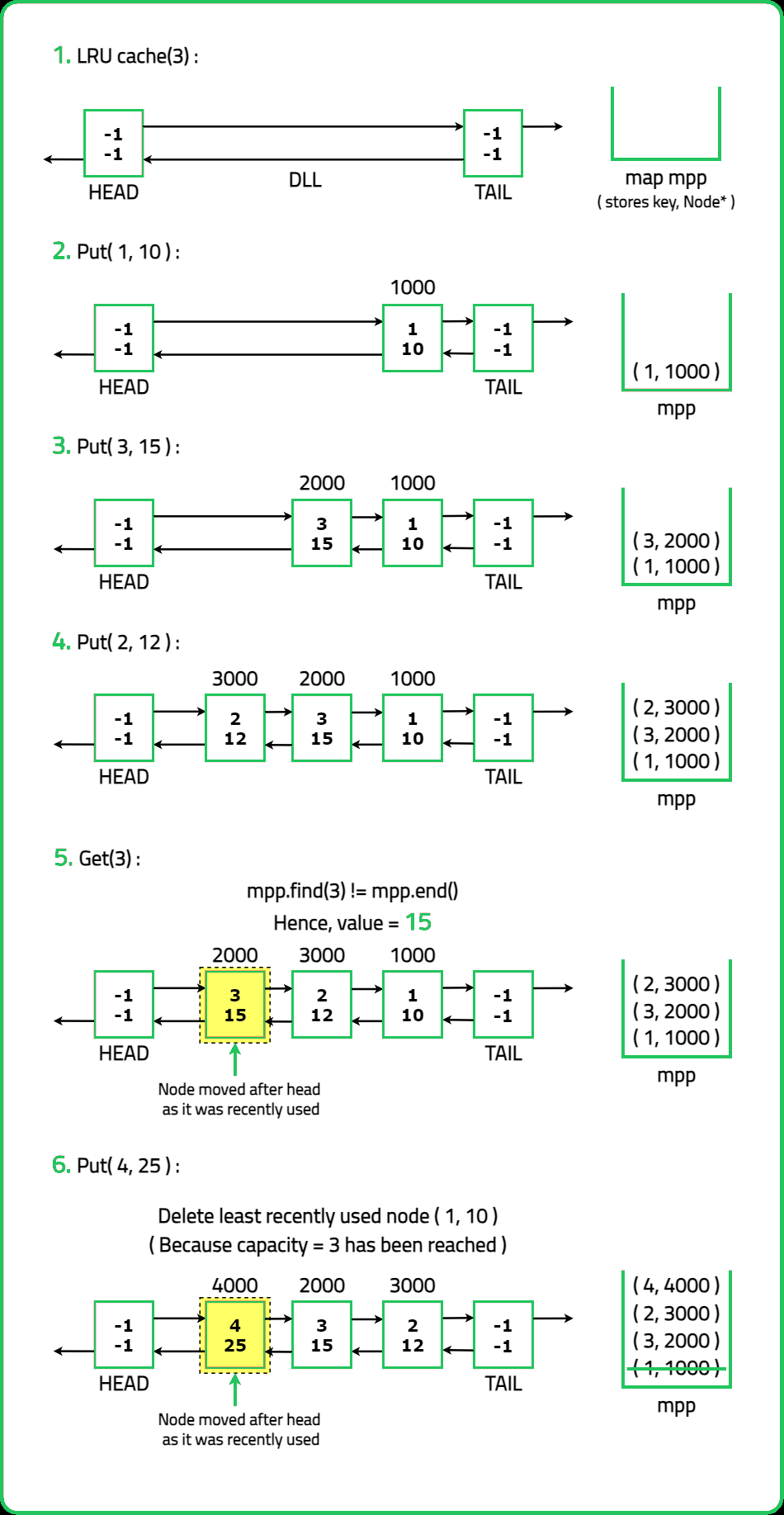
Design a data structure that follows the constraints of Least Recently Used (LRU) cache.
Implement the LRUCache class:
LRUCache(int capacity): We need to initialize the LRU cache with positive size capacity.
int get(int key): Returns the value of the key if the key exists, otherwise return -1.
void put(int key,int value): Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.
The functions get and put must each run in O(1) average time complexity.
Examples:
Input:
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[ [2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4] ]
Output:
[null, null, null, 1, null, -1, null, -1, 3, 4]
Explanation:
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
Input:
["LRUCache", "put", "put", "get", "put", "get", "put", "get"]
[[1], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [3]]
Output:
[null, null, null, -1, null, -1, null, -1]
Explanation:
LRUCache lRUCache = new LRUCache(1);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // evicts key 1, cache is {2=2}
lRUCache.get(1); // returns -1 (not found)
lRUCache.put(3, 3); // evicts key 2, cache is {3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // evicts key 3, cache is {4=4}
lRUCache.get(3); // returns -1 (not found)
Input:
["LRUCache", "put", "put", "get", "put", "put", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [4, 4], [2], [4]]
Constraints
- 1 <= capacity <= 1000
- 0 <= key <= 104
- 0 <= value <= 105
- At most 105 calls will be made to get and put.
Hints
- A brute-force approach would involve a list or an array, but searching for a key or maintaining usage order requires O(n) complexity.
- HashMap (key -> Node) for O(1) lookups. Doubly Linked List to track the most recently used (MRU) and least recently used (LRU) elements. head (MRU) → most recently accessed item. tail (LRU) → least recently used item (to be removed when the cache exceeds capacity).