GCD of two numbers
Beginner Problems
Basic Maths
Easy
- Here's a fun fact: the concept of finding the Greatest Common Divisor (GCD) is used in real-world encryption algorithms, particularly in RSA encryption
- RSA, which stands for Rivest-Shamir-Adleman, is a public key encryption technology used widely in securing sensitive data, especially when being sent over an insecure network
- It involves the use of large prime numbers, and the computation of their GCD, to generate secure public and private keys
- So, the algorithm to solve this programming problem is integral to promoting online security and privacy
You are given two integers n1 and n2. You need find the Greatest Common Divisor (GCD) of the two given numbers. Return the GCD of the two numbers.
The Greatest Common Divisor (GCD) of two integers is the largest positive integer that divides both of the integers.
Examples:
Input: n1 = 4, n2 = 6
Output: 2
Explanation: Divisors of n1 = 1, 2, 4, Divisors of n2 = 1, 2, 3, 6
Greatest Common divisor = 2.
Input: n1 = 9, n2 = 8
Output: 1
Explanation: Divisors of n1 = 1, 3, 9 Divisors of n2 = 1, 2, 4, 8.
Greatest Common divisor = 1.
Input: n1 = 6, n2 = 12
Constraints
- 1 <= n1, n2 <= 1000
Company Tags
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro
IBM
HCL
Tech Mahindra
MindTree
Editorial
Intuition:
The GCD (Greatest Common Divisor), also known as HCF (Highest Common Factor), of two numbers is the largest number that divides both without leaving a remainder. To find the GCD, check all numbers from 1 up to the smaller of the two input numbers for common factors. The largest of these common factors is the GCD.
Approach:
- Initialize a variable
gcdwith 1 that will store the greatest common divisor of the two given numbers. - Iterate from 1 to the minimum of the two numbers using a loop variable. Update the
gcdif both the given numbers are divisible by the current value of the loop variable. - After the iterations are over, the greatest common divisor will be stored in the
gcdvariable.
Dry Run:
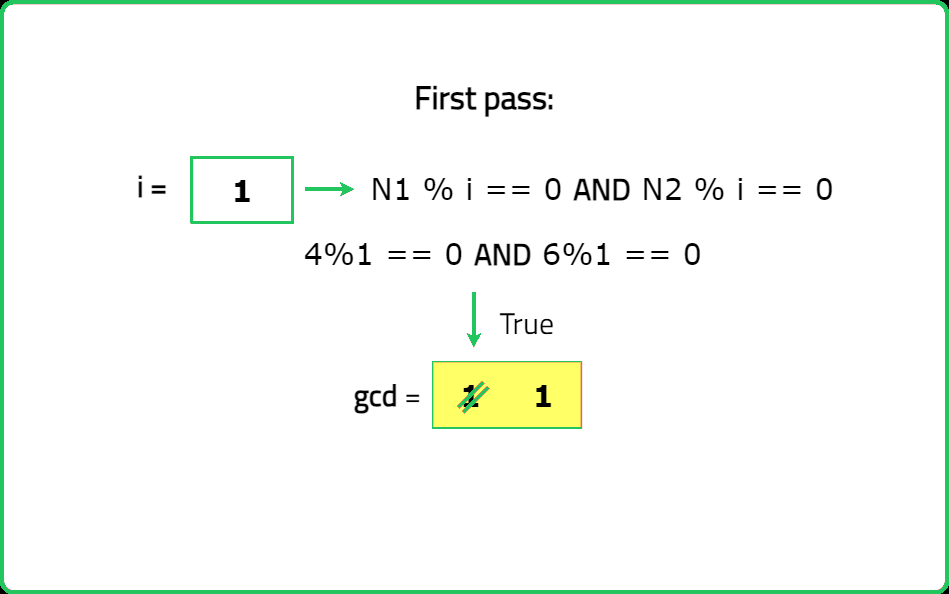
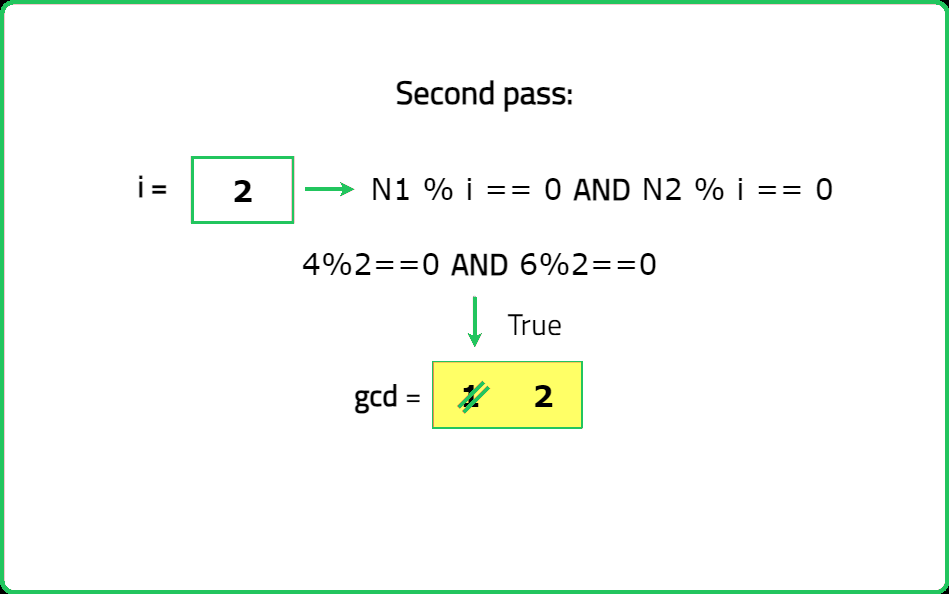
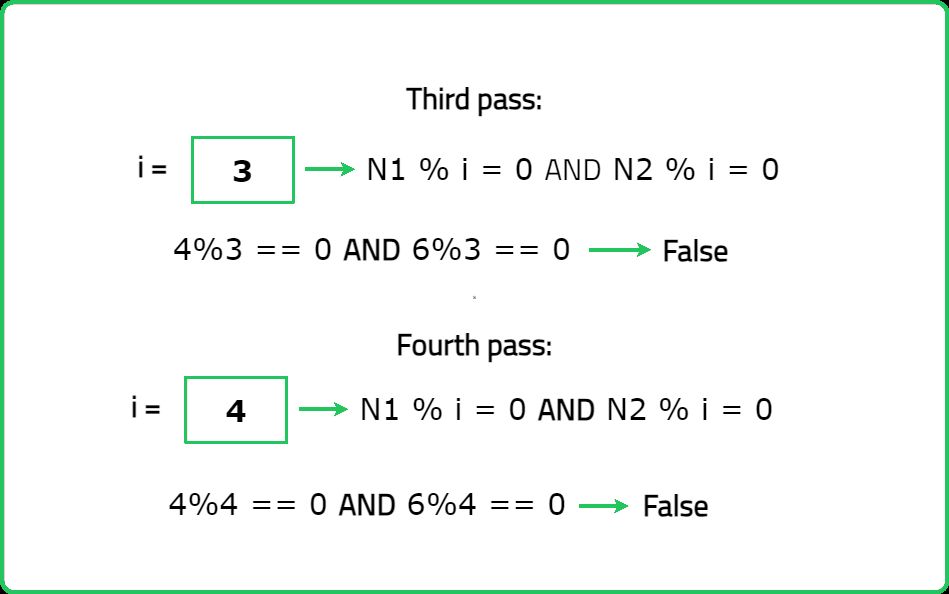
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the
GCD of two numbers */
int GCD(int n1, int n2) {
// Variable to store the gcd
int gcd = 1;
// Iterate from 1 to min(n1, n2)
for(int i = 1; i <= min(n1, n2); i++) {
/* Check if i is a common
divisor of both n1 and n2 */
if(n1 % i == 0 && n2 % i == 0) {
// Update gcd
gcd = i;
}
}
// Return stored GCD.
return gcd;
}
};
int main() {
int n1 = 4, n2 = 6;
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the
gcd of two numbers */
int ans = sol.GCD(n1, n2);
cout << "GCD of " << n1 << " and " << n2 << " is: " << ans << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839
class Solution {
/* Function to find the
GCD of two numbers */
public int GCD(int n1, int n2) {
// Variable to store the gcd
int gcd = 1;
// Iterate from 1 to min(n1, n2)
for(int i = 1; i <= Math.min(n1, n2); i++) {
/* Check if i is a common
divisor of both n1 and n2 */
if(n1 % i == 0 && n2 % i == 0) {
// Update gcd
gcd = i;
}
}
// Return stored GCD.
return gcd;
}
public static void main(String[] args) {
int n1 = 4, n2 = 6;
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the
gcd of two numbers */
int ans = sol.GCD(n1, n2);
System.out.println("GCD of " + n1 + " and " + n2 + " is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435
class Solution:
# Function to find the
# GCD of two numbers
def GCD(self, n1, n2):
# Variable to store the gcd
gcd = 1
# Iterate from 1 to min(n1, n2)
for i in range(1, min(n1, n2) + 1):
# Check if i is a common
# divisor of both n1 and n2
if n1 % i == 0 and n2 % i == 0:
# Update gcd
gcd = i
# Return stored GCD.
return gcd
# Input numbers
n1 = 4
n2 = 6
# Creating an instance of
# Solution class
sol = Solution()
# Function call to find the
# gcd of two numbers
ans = sol.GCD(n1, n2)
print(f"GCD of {n1} and {n2} is: {ans}")
123456789101112131415161718192021222324252627282930313233343536373839
class Solution {
/* Function to find the
GCD of two numbers */
GCD(n1, n2) {
// Variable to store the gcd
let gcd = 1;
// Iterate from 1 to min(n1, n2)
for (let i = 1; i <= Math.min(n1, n2); i++) {
/* Check if i is a common
divisor of both n1 and n2 */
if (n1 % i === 0 && n2 % i === 0) {
// Update gcd
gcd = i;
}
}
// Return stored GCD.
return gcd;
}
}
// Input numbers
let n1 = 4;
let n2 = 6;
/* Creating an instance of
Solution class */
let sol = new Solution();
/* Function call to find the
gcd of two numbers */
let ans = sol.GCD(n1, n2);
console.log(`GCD of ${n1} and ${n2} is: ${ans}`);
Complexity Analysis:
Time Complexity: O(min(N1, N2)) – where N1 and N2 are given numbers. Iterating from 1 to min(N1, N2) and performing constant time operations in each iteration.
Space Complexity: O(1) – Using a couple of variables i.e., constant space.
Intuition:
The time complexity of the previous approach can be optimized if we iterate backward from min(n1, n2) to 1. This way the first divisor that is found for both numbers can be returned as the greatest common divisor of the numbers saving unnecessary iterations.
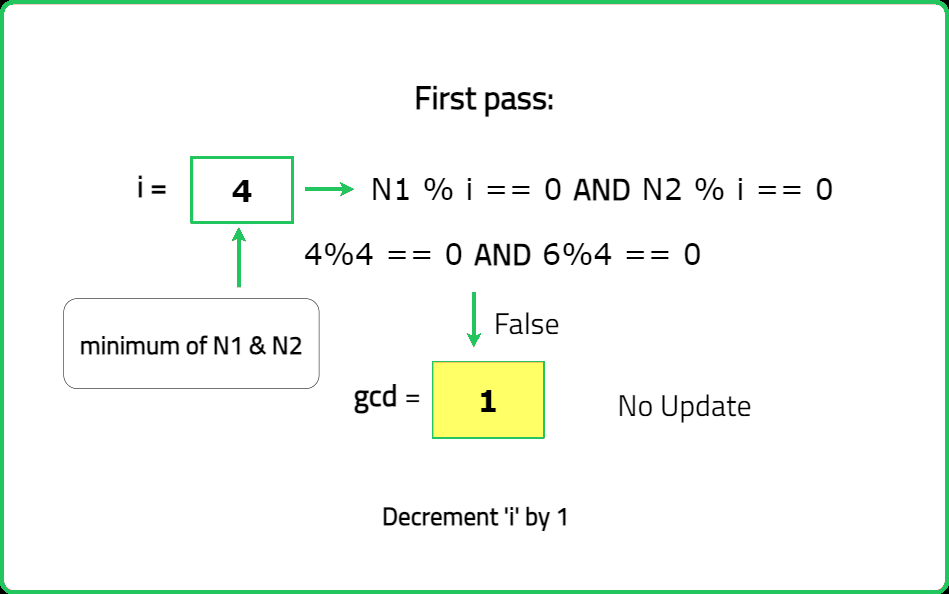
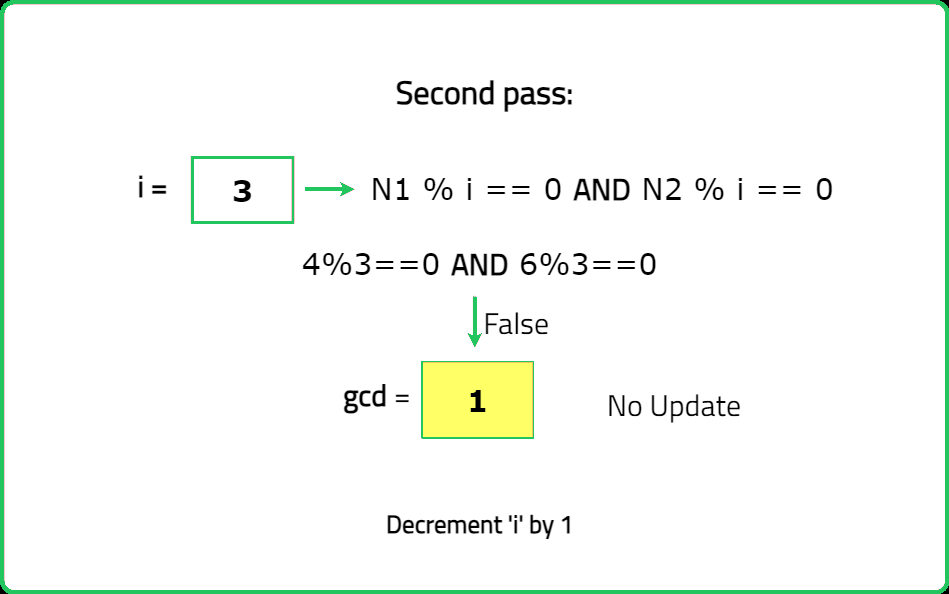
Approach:
- Declare a variable
gcdthat will store the greatest common divisor of the two given numbers. - Iterate from the minimum of the two numbers down to 1 using a loop variable. Update the
gcdif both the given numbers are divisible by the current value of the loop variable and break out from the loop to save unnecessary iterations. - The greatest common divisor for the two numbers is stored in the
gcdvariable which can be returned as the answer.
Dry Run:
Solution:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the
GCD of two numbers*/
int GCD(int n1, int n2) {
// Variable to store the gcd
int gcd;
// Iterate from 1 to min(n1, n2)
for(int i = min(n1, n2); i >= 1; --i) {
/* Check if i is a common
divisor of both n1 and n2 */
if(n1 % i == 0 && n2 % i == 0) {
// Update gcd
gcd = i;
// Break to skip unnecessary iterations
break;
}
}
// Return stored GCD.
return gcd;
}
};
int main() {
int n1 = 4, n2 = 6;
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the
gcd of two numbers */
int ans = sol.GCD(n1, n2);
cout << "GCD of " << n1 << " and " << n2 << " is: " << ans << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041
class Solution {
/* Function to find the
GCD of two numbers */
public int GCD(int n1, int n2) {
// Variable to store the gcd
int gcd = 1;
// Iterate from 1 to min(n1, n2)
for (int i = Math.min(n1, n2); i >= 1; --i) {
/* Check if i is a common
divisor of both n1 and n2 */
if (n1 % i == 0 && n2 % i == 0) {
// Update gcd
gcd = i;
// Break to skip unnecessary iterations
break;
}
}
// Return stored GCD.
return gcd;
}
public static void main(String[] args) {
int n1 = 4, n2 = 6;
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the
gcd of two numbers */
int ans = sol.GCD(n1, n2);
System.out.println("GCD of " + n1 + " and " + n2 + " is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233
class Solution:
# Function to find the GCD of two numbers
def GCD(self, n1, n2):
# Variable to store the gcd
gcd = 1
# Iterate from 1 to min(n1, n2)
for i in range(min(n1, n2), 0, -1):
# Check if i is a common divisor
# of both n1 and n2
if n1 % i == 0 and n2 % i == 0:
# Update gcd
gcd = i
# Break to skip unnecessary iterations
break
# Return stored GCD
return gcd
# Input numbers
n1, n2 = 4, 6
# Creating an instance of Solution class
sol = Solution()
# Function call to find the gcd of two numbers
ans = sol.GCD(n1, n2)
print(f"GCD of {n1} and {n2} is: {ans}")
12345678910111213141516171819202122232425262728293031323334353637383940
class Solution {
/* Function to find the
GCD of two numbers */
GCD(n1, n2) {
// Variable to store the gcd
let gcd = 1;
// Iterate from 1 to min(n1, n2)
for (let i = Math.min(n1, n2); i >= 1; --i) {
/* Check if i is a common
divisor of both n1 and n2 */
if (n1 % i === 0 && n2 % i === 0) {
// Update gcd
gcd = i;
// Break to skip unnecessary iterations
break;
}
}
// Return stored GCD.
return gcd;
}
}
// Input numbers
let n1 = 4, n2 = 6;
/* Creating an instance of
Solution class */
let sol = new Solution();
/* Function call to find the
gcd of two numbers */
let ans = sol.GCD(n1, n2);
console.log(`GCD of ${n1} and ${n2} is: ${ans}`);
Complexity Analysis:
Time Complexity: O(min(N1, N2)) – where N1 and N2 are given numbers. In the worst case, finding GCD will require iterating from min(N1, N2) till 1 and performing constant time operations in each iteration.
Space Complexity: O(1) – Using a couple of variables i.e., constant space.
Intuition:
The most optimal way to solve this problem is to use the Euclidean Algorithm which works on the principle that the GCD of two numbers remains the same even if the smaller number is subtracted from the larger number.
Euclidean Algorithm:
To find the GCD of n1 and n2 where n1 > n2:- Repeatedly subtract the smaller number from the larger number until one of them becomes 0.
- Once one of them becomes 0, the other number is the GCD of the original numbers.
Example: GCD of n1 = 7, n2 = 2 can be found in this way:
- gcd(7, 2) = gcd(7-2, 2) = gcd(5, 2)
gcd(5, 2) = gcd(5-2, 2) = gcd(3, 2)
gcd(3, 2) = gcd(3-2, 2) = gcd(1, 2) -
gcd(2, 1) = gcd(2-1, 1) = gcd(1, 1)
gcd(1, 1) = gcd(1-1, 1) = gcd(0, 1) - Hence GCD of n1 = 7, n2 = 2 is 1.
Note:
Observe that instead of subtracting the smaller number from the greater number repeatedly, the modulus operator can be used.gcd(7, 2) = gcd(7%2, 2) = gcd(1, 2)
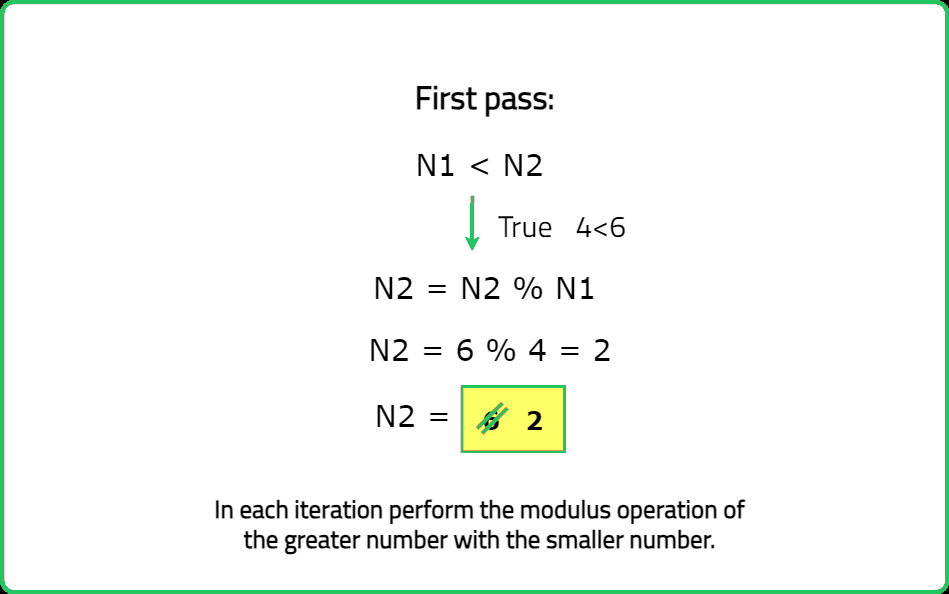
Approach:
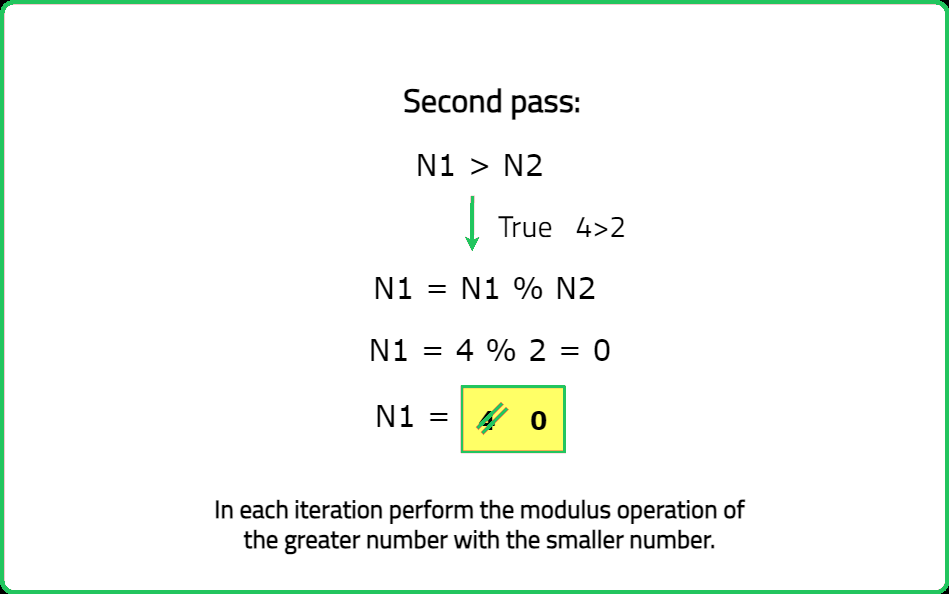
- Initialize a while loop till both numbers are greater than zero.
- In each iteration perform the modulus operation of the greater number with the smaller number.
- Once the loop terminates, one of the two variables stores a non-zero value which is the GCD for the given pair of numbers.
Dry Run:
Solution:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the
GCD of two numbers*/
int GCD(int n1, int n2) {
/* Continue loop as long as both
n1 and n2 are greater than zero */
while(n1 > 0 && n2 > 0) {
/* If n1 is greater than n2, perform
modulo operation - n1 % n2 */
if(n1 > n2) {
n1 = n1 % n2;
}
/* Else perform modulo
operation - n2 % n1 */
else {
n2 = n2 % n1;
}
}
// If n1 is zero, GCD is stored in n2
if(n1 == 0) return n2;
//else GCD is stored in n1
return n1;
}
};
int main() {
int n1 = 4, n2 = 6;
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the
gcd of two numbes */
int ans = sol.GCD(n1, n2);
cout << "GCD of " << n1 << " and " << n2 << " is: " << ans << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344
class Solution {
/* Function to find the
GCD of two numbers */
public int GCD(int n1, int n2) {
/* Continue loop as long as both
n1 and n2 are greater than zero */
while (n1 > 0 && n2 > 0) {
/* If n1 is greater than n2, perform
modulo operation - n1 % n2 */
if (n1 > n2) {
n1 = n1 % n2;
}
/* Else perform modulo
operation - n2 % n1 */
else {
n2 = n2 % n1;
}
}
// If n1 is zero, GCD is stored in n2
if (n1 == 0) return n2;
//else GCD is stored in n1
return n1;
}
public static void main(String[] args) {
int n1 = 4, n2 = 6;
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the
gcd of two numbes */
int ans = sol.GCD(n1, n2);
System.out.println("GCD of " + n1 + " and " + n2 + " is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536
class Solution:
# Function to find the GCD of two numbers
def GCD(self, n1, n2):
# Continue loop as long as both n1 and
# n2 are greater than zero
while n1 > 0 and n2 > 0:
# If n1 is greater than n2, perform
# modulo operation - n1 % n2
if n1 > n2:
n1 = n1 % n2
# Else perform modulo operation - n2 % n1
else:
n2 = n2 % n1
# If n1 is zero, GCD is stored in n2
if n1 == 0:
return n2
# else GCD is stored in n1
return n1
# Input numbers
n1 = 4
n2 = 6
# Creating an instance of Solution class
sol = Solution()
# Function call to find the gcd of two numbers
ans = sol.GCD(n1, n2)
print("GCD of", n1, "and", n2, "is:", ans)
1234567891011121314151617181920212223242526272829303132333435363738394041
class Solution {
/* Function to find the
GCD of two numbers */
GCD(n1, n2) {
/* Continue loop as long as both
n1 and n2 are greater than zero */
while (n1 > 0 && n2 > 0) {
/* If n1 is greater than n2, perform
modulo operation - n1 % n2 */
if (n1 > n2) {
n1 = n1 % n2;
}
/* Else perform modulo
operation - n2 % n1 */
else {
n2 = n2 % n1;
}
}
// If n1 is zero, GCD is stored in n2
if (n1 === 0) return n2;
// else GCD is stored in n1
return n1;
}
}
// Input numbers
let n1 = 4, n2 = 6;
// Creating an instance of Solution class
let sol = new Solution();
// Function call to find the gcd of two numbers
let ans = sol.GCD(n1, n2);
console.log("GCD of " + n1 + " and " + n2 + " is: " + ans);
Complexity Analysis:
Time Complexity: O(log(min(N1, N2))) – where N1 and N2 are given numbers. Because in every iteration, the algorithm is dividing larger number with the smaller number resulting in time complexity.(approx.)
Space Complexity: O(1) – Using a couple of variables i.e., constant space.
Notes
Code
✅ Testcase
Input: {'n1': '4', 'n2': '6'}
Expected:
2
2
Actual: -
Time: -
sec
Status: Waiting
Input: {'n1': '9', 'n2': '8'}
Expected:
1
1
Actual: -
Time: -
sec
Status: Waiting
Input: {'n1': '15', 'n2': '18'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting