Palindrome partitioning

Recursion FAQs (Hard) Hard

Fun Fact: This problem concept is heavily applied in building AI chatbots, particularly for checking if a sentence or phrase is the same forward and backward, an example of a palindrome
Natural language processing (NLP) is a massive part of AI chatbots that can parse, understand, and respond to user input in a way that simulates natural human conversation - the palindrome partitioning helps in this case
Besides, it's also used in DNA sequence analysis in bioinformatics, where analyzing palindromic sequences can play a critical role in understanding DNA sequences and their functions

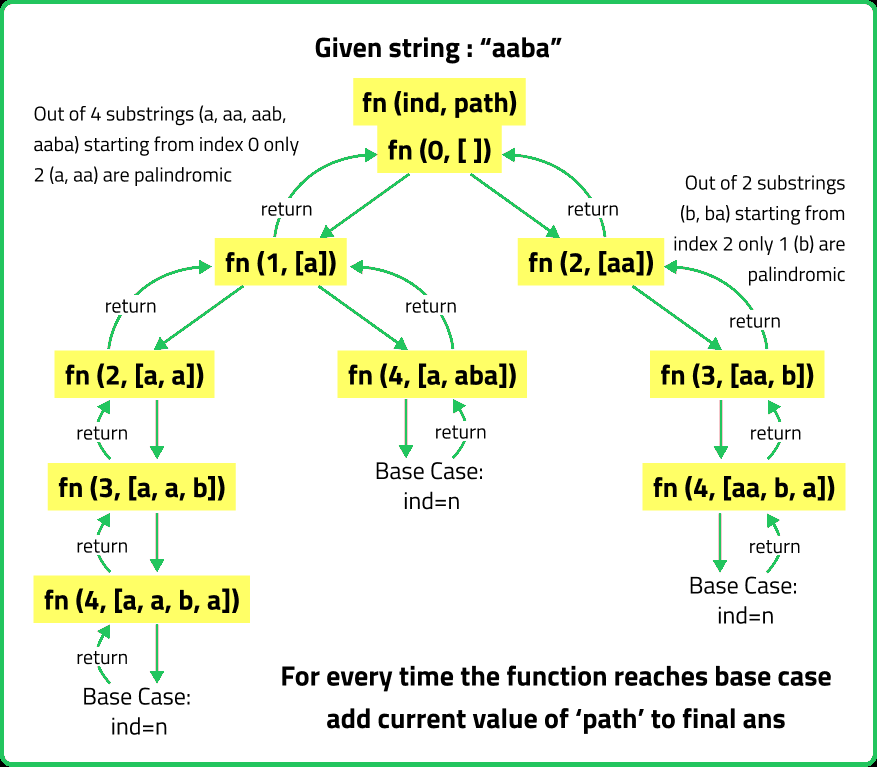
Given a string s partition string s such that every substring of partition is palindrome. Return all possible palindrome partition of string s.

Examples:

Input : s = "aabaa"

Output : [ [ "a", "a", "b", "a", "a"] , [ "a", "a", "b", "aa"] , [ "a", "aba", "a"] , [ "aa", "b", "a", "a"] , [ "aa", "b", "aa" ] , [ "aabaa" ] ]

Explanation : Above all are the possible ways in which the string can be partitioned so that each substring is a palindrome.

Input : s = "baa"

Output : [ [ "b", "a", "a"] , [ "b", "aa" ] ]

Explanation : Above all are the possible ways in which the string can be partitioned so that each substring is a palindrome.

Input : s = "ab"

Constraints

1<= s.length <= 16
s contains only lowercase English letters.

Hints

Use recursion to explore all possible partitions. Backtrack to remove the last added substring and try other possibilities.
Use a helper function to check if a substring is a palindrome.

Company Tags

Instacart PayPal Airbnb Walmart American Express Shopify Medtronic Seagate Technology Cloudflare Morgan Stanley Siemens Healthineers Qualcomm Unity Technologies Electronic Arts Pinterest Mastercard PwC Robinhood Salesforce Stripe Visa Ubisoft Wayfair Byju's Freshworks Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Real-life Example

Imagine organizing a long sentence into meaningful phrases. Start at the beginning, find a segment that forms a meaningful phrase, and write it down. Move to the next segment and repeat the process. If reaching the end of the sentence and having a list of meaningful phrases, the job is done. If stuck, erase the last phrase, try a different segment, and continue until all segments are explored and every possible meaningful combination is found.

Recursion Intuition

The process involves breaking down a problem into smaller sub-problems. Begin at the start of a string and identify palindromic substrings. Record a substring and proceed to the next part of the string. Continue this process until the end of the string. If the end is reached, a valid partition is found and stored. If a valid partition is not found, backtrack by removing the last recorded substring and try a different substring, exploring all possible palindromic partitions.

Approach

Initialize an empty result list to store all possible partitions.
Define a recursive function that takes the current index, the string, a temporary path list, and the result list.
In the recursive function, check if the current index has reached the end of the string, if true, add the current path to the result list and return. If false, iterate over the substring starting from the current index.
For each substring, check if it is a palindrome, if true, add the substring to the current path. Call the recursive function with the next index. Backtrack by removing the last added substring to explore other possibilities.
Define a helper function to check if a given substring is a palindrome Compare characters from the start and end of the substring. If all characters match, the substring is a palindrome.
Invoke the recursive function initially with the starting index, the string, an empty path list, and the result list. Return the result list containing all possible palindromic partitions.

Dry Run

Solution

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    vector<vector<string>> partition(string s) {
        // Resultant vector to store all partitions
        vector<vector<string>> res;
        // Temporary vector to store current partition
        vector<string> path;
        // Start the depth-first search from index 0
        dfs(0, s, path, res);
        return res;
    }

    void dfs(int index, string s, vector<string> &path, vector<vector<string>> &res) {
        // If the index reaches the end of the string
        if (index == s.size()) {
            // Add the current partition to the result
            res.push_back(path);
            return;
        }
        // Iterate over the substring starting from 'index'
        for (int i = index; i < s.size(); ++i) {
            // Check if the substring s[index..i] is a palindrome
            if (isPalindrome(s, index, i)) {
                // If true, add it to the current path
                path.push_back(s.substr(index, i - index + 1));
                // Recur for the remaining substring
                dfs(i + 1, s, path, res);
                // Backtrack: remove the last added substring
                path.pop_back();
            }
        }
    }

    bool isPalindrome(string s, int start, int end) {
        // Check if the substring s[start..end] is a palindrome
        while (start <= end) {
            // If characters do not match, it's not a palindrome
            if (s[start++] != s[end--])
                return false;
        }
        return true; // Otherwise, it's a palindrome
    }
};

// Main method for testing
int main() {
    Solution solution;
    string s = "aab";
    vector<vector<string>> result = solution.partition(s);
    for (const auto& partition : result) {
        for (const auto& str : partition) {
            cout << str << " ";
        }
        cout << endl;
    }
    return 0;
}
import java.util.ArrayList;
import java.util.List;

class Solution {
    public List<List<String>> partition(String s) {
        // Resultant list to store all partitions
        List<List<String>> res = new ArrayList<>();
        // Temporary list to store current partition
        List<String> path = new ArrayList<>();
        // Start the depth-first search from index 0
        dfs(0, s, path, res);
        return res;
    }

    private void dfs(int index, String s, List<String> path, List<List<String>> res) {
        // If the index reaches the end of the string
        if (index == s.length()) {
            // Add the current partition to the result
            res.add(new ArrayList<>(path));
            return;
        }
        // Iterate over the substring starting from 'index'
        for (int i = index; i < s.length(); i++) {
            // Check if the substring s[index..i] is a palindrome
            if (isPalindrome(s, index, i)) {
                // If true, add it to the current path
                path.add(s.substring(index, i + 1));
                // Recur for the remaining substring
                dfs(i + 1, s, path, res);
                // Backtrack: remove the last added substring
                path.remove(path.size() - 1);
            }
        }
    }

    private boolean isPalindrome(String s, int start, int end) {
        // Check if the substring s[start..end] is a palindrome
        while (start <= end) {
            // If characters do not match, it's not a palindrome
            if (s.charAt(start++) != s.charAt(end--))
                return false;
        }
        return true; // Otherwise, it's a palindrome
    }

    // Main method for testing
    public static void main(String[] args) {
        Solution solution = new Solution();
        String s = "aab";
        List<List<String>> result = solution.partition(s);
        for (List<String> partition : result) {
            System.out.println(partition);
        }
    }
}
class Solution:
    def partition(self, s: str):
        def dfs(index, path):
            # If index reaches the end of the string
            if index == len(s):
                # Add the current partition to the result
                res.append(path[:])
                return
            # Iterate over the substring starting from 'index'
            for i in range(index, len(s)):
                # Check if the substring s[index..i] is a palindrome
                if isPalindrome(index, i):
                    # If true, add it to the current path
                    path.append(s[index:i+1])
                    # Recur for the remaining substring
                    dfs(i+1, path)
                    # Backtrack: remove the last added substring
                    path.pop()

        def isPalindrome(start, end):
            # Check if the substring s[start..end] is a palindrome
            while start <= end:
                # If characters do not match, it's not a palindrome
                if s[start] != s[end]:
                    return False
                start += 1
                end -= 1
            return True # Otherwise, it's a palindrome

        # Resultant list to store all partitions
        res = []
        # Start the depth-first search from index 0
        dfs(0, [])
        return res

# Main method for testing
if __name__ == "__main__":
    solution = Solution()
    s = "aab"
    result = solution.partition(s)
    for partition in result:
        print(partition)
class Solution {
    partition(s) {
        // Resultant array to store all partitions
        const res = [];
        // Temporary array to store the current partition
        const path = [];
        // Start the depth-first search from index 0
        this.dfs(0, s, path, res);
        return res;
    }

    dfs(index, s, path, res) {
        // If the index reaches the end of the string
        if (index === s.length) {
            // Add the current partition to the result
            res.push([...path]);
            return;
        }
        // Iterate over the substring starting from 'index'
        for (let i = index; i < s.length; ++i) {
            // Check if the substring s[index..i] is a palindrome
            if (this.isPalindrome(s, index, i)) {
                // If true, add it to the current path
                path.push(s.substring(index, i + 1));
                // Recur for the remaining substring
                this.dfs(i + 1, s, path, res);
                // Backtrack: remove the last added substring
                path.pop();
            }
        }
    }

    isPalindrome(s, start, end) {
        // Check if the substring s[start..end] is a palindrome
        while (start <= end) {
            // If characters do not match, it's not a palindrome
            if (s[start++] !== s[end--]) {
                return false;
            }
        }
        return true; // Otherwise, it's a palindrome
    }
}

// Main method for testing
const solution = new Solution();
const s = "aab";
const result = solution.partition(s);
result.forEach(partition => {
    console.log(partition);
});

Complexity Analysis

Time Complexity : The time complexity is O(2^N) due to the exponential number of possible partitions.

Space Complexity : The space complexity is O(N) for the recursion stack and additional space for storing partitions.

Code

Problem List