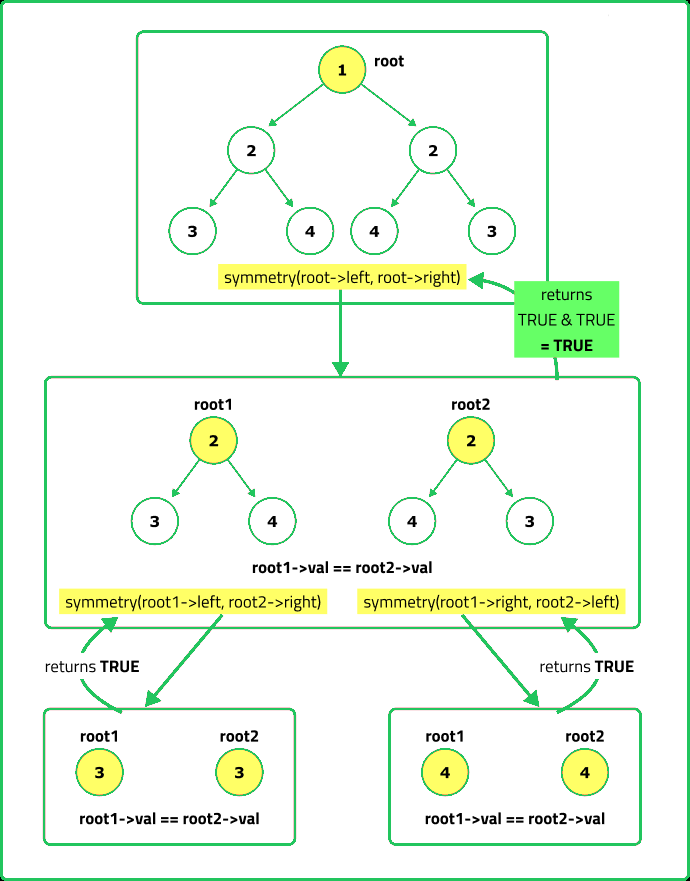
Check for symmetrical BTs
Binary Trees
Medium Problems
Medium
- Fun fact: The concept of checking for symmetry in a binary tree, or verifying if a structure is a mirror image of itself, is applied in compilers or syntax checkers of Integrated Development Environments (IDEs)
- These tools often need to parse and analyze code syntax trees and confirm their correctness
- Ensuring their symmetry can be a part of validating that code has been written in a balanced and structured way, thus optimizing the compiler's performance and improving code execution
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Examples:
Input : root = [1, 2, 2, 3, 4, 4, 3]
Output : true
Explanation :

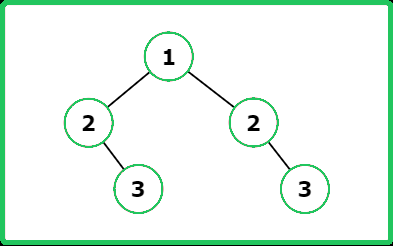
Input : root = [1, 2, 2, null, 3, null, 3]
Output : false
Explanation : When a straight line is drawn through the root node and the tree is folded around it, the rightmost node 3 is overlapped with null node and the node 3 present at left of root node is overlapped with null nodes.
So both node 3 in tree does not show symmetric behaviour.
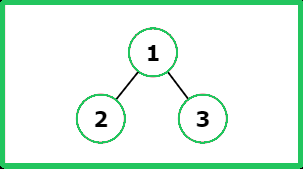
Input: root = [1, 2, 3]
Constraints
- 1<= Number of Nodes <= 104
- -100 <= Node.val <= 100
Hints
- A recursive approach naturally fits this problem. Check if both the left and right children exist. Ensure that their values are equal and recursively compare
- An iterative approach can be implemented using a queue (BFS) or stack (DFS) by processing nodes in pairs. Instead of recursion, push nodes into a queue in mirror order and check symmetry level by level.
Company Tags
Snowflake
Uber
Optum
Epic Systems
Byju's
Boston Consulting Group
Micron Technology
NVIDIA
Western Digital
Robinhood
MongoDB
IBM
PwC
PayPal
Teladoc Health
Oracle
Flipkart
Ubisoft
Electronic Arts
Dropbox
eBay
AMD
DoorDash
Epic Games
Alibaba
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe