123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139
#include <bits/stdc++.h>
using namespace std;
// Class representing each node of the Trie
class Node {
public:
// To store references to child nodes
Node* links[26];
// Flag to indicate end of a word
bool flag = false;
// Checks if the current character link exists
bool containsKey(char ch) {
return (links[ch - 'a'] != NULL);
}
// Returns the next node corresponding to the character
Node* get(char ch) {
return links[ch - 'a'];
}
// Creates a link to the next node for the current character
void put(char ch, Node* node) {
links[ch - 'a'] = node;
}
// Marks the end of a word
void setEnd() {
flag = true;
}
// Checks if the current node is the end of a word
bool isEnd() {
return flag;
}
};
// Class representing the Trie (Prefix Tree) structure
class Trie {
public:
// Root node of the Trie
Node* root;
// Initializes the Trie
Trie() {
root = new Node();
}
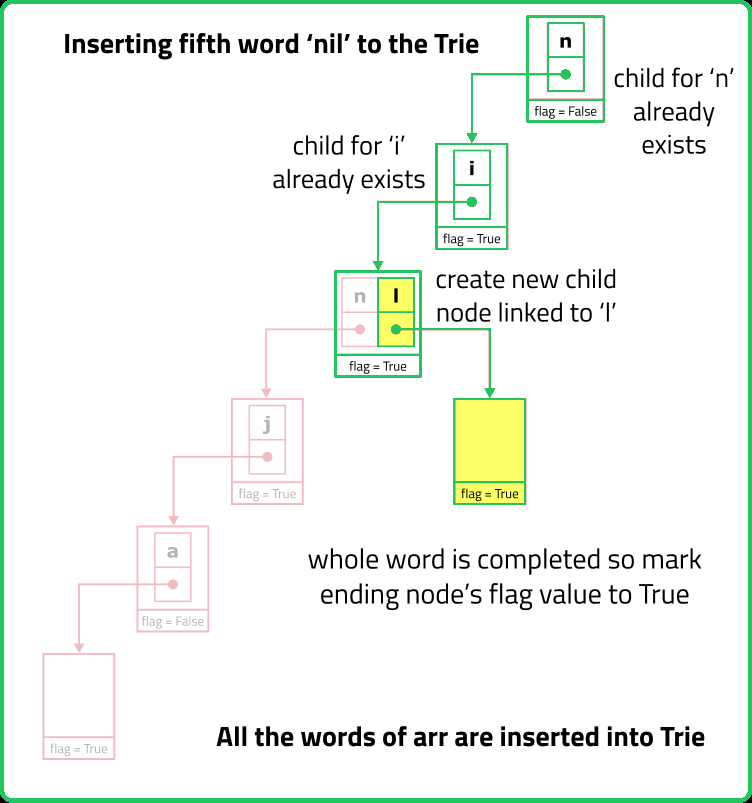
// Inserts a word into the Trie
void insert(string word) {
Node* node = root;
for (int i = 0; i < word.size(); i++) {
if (!node->containsKey(word[i])) {
node->put(word[i], new Node());
}
node = node->get(word[i]);
}
// Marks the end of the inserted word
node->setEnd();
}
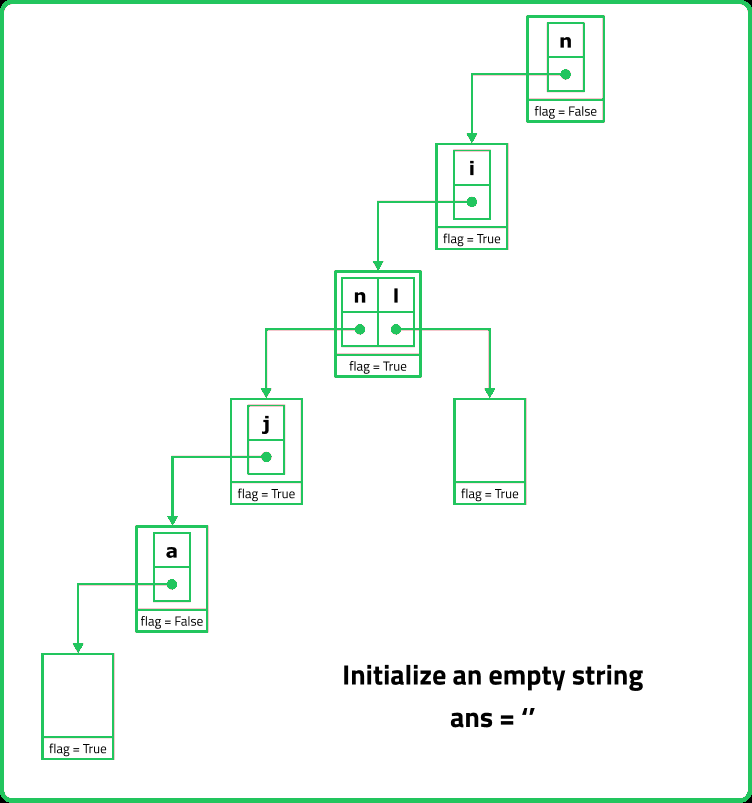
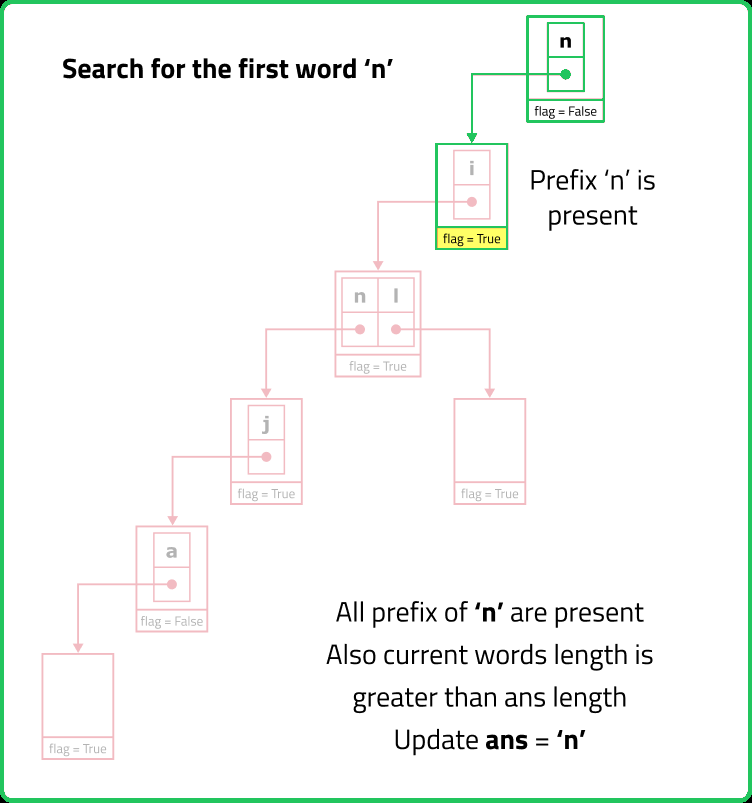
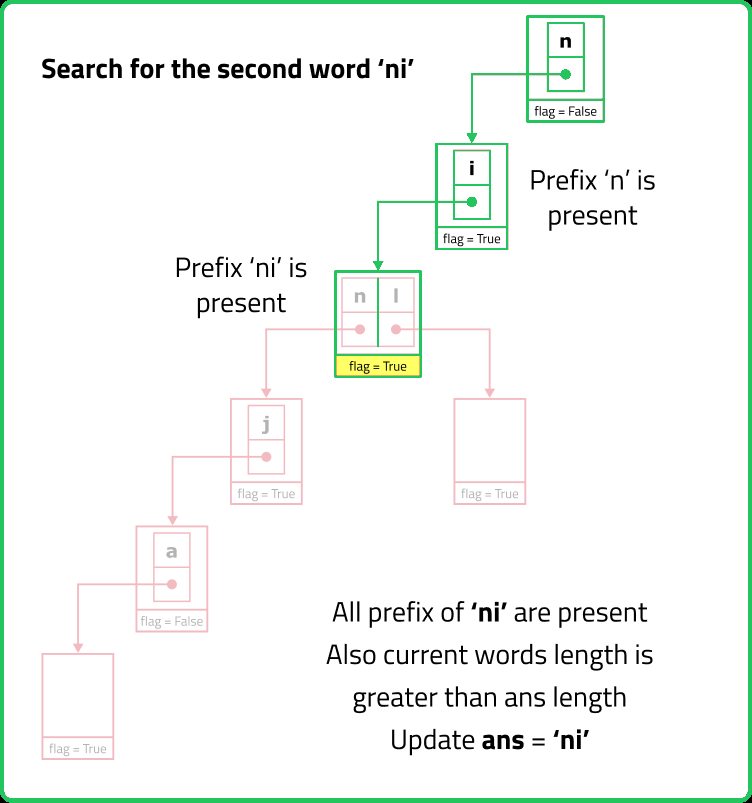
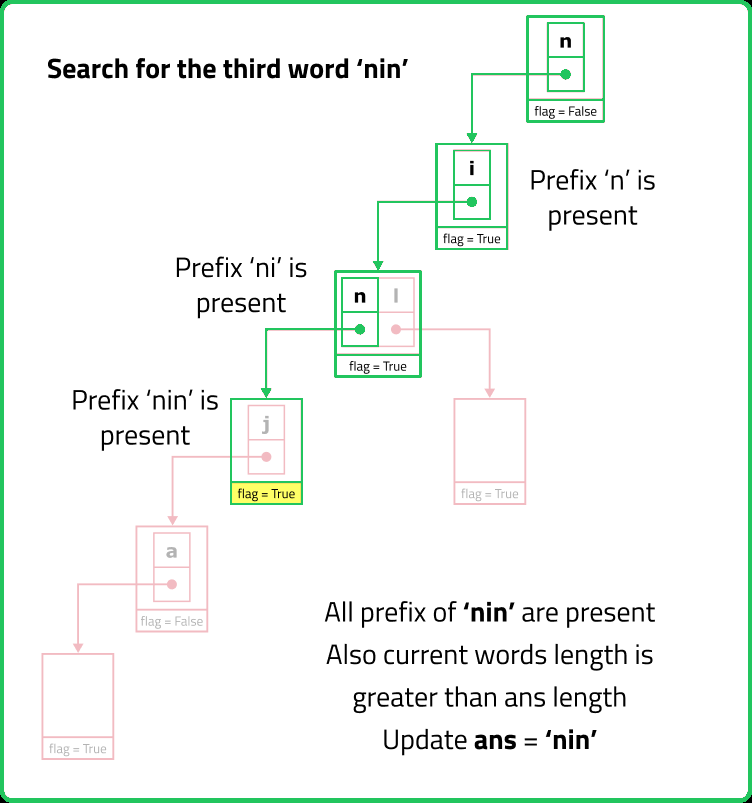
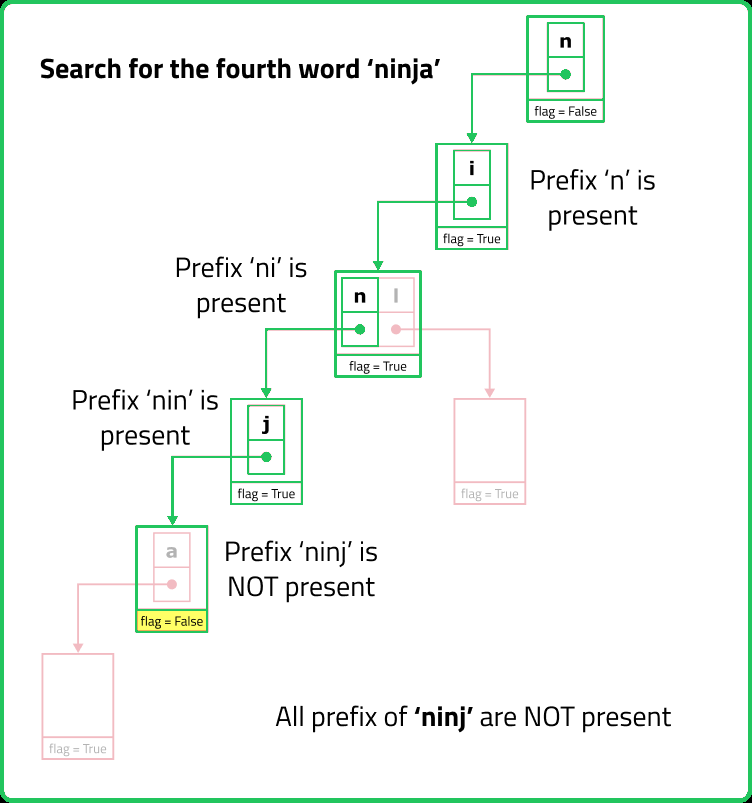
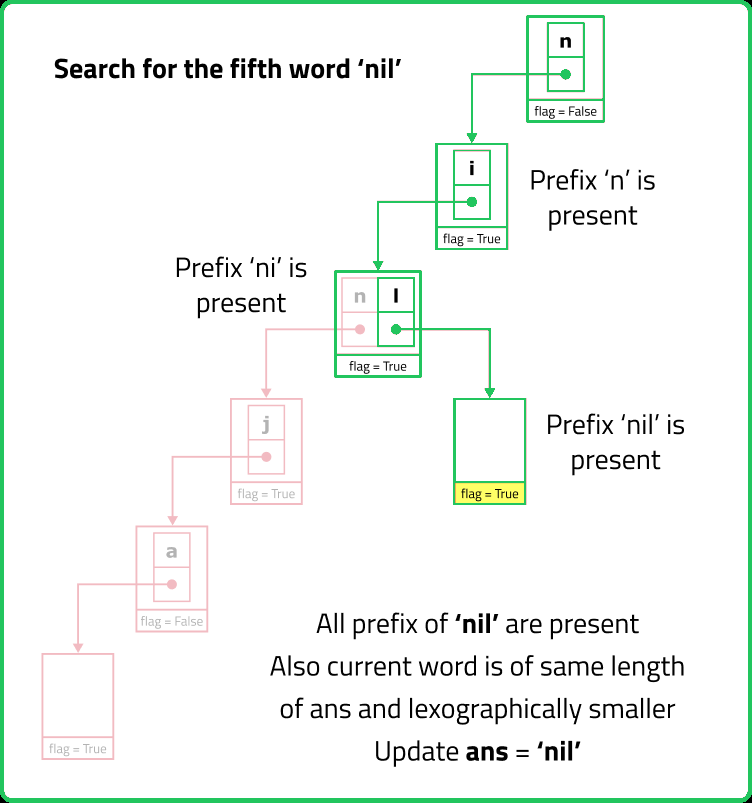
// Checks if all prefixes of the given word exist in the Trie
bool checkIfAllPrefixExists(string word) {
Node* node = root;
for (int i = 0; i < word.size(); i++) {
if (node->containsKey(word[i])) {
node = node->get(word[i]);
if (!node->isEnd()) {
// Prefix is incomplete, return false
return false;
}
} else {
// Return false if a character link is missing
return false;
}
}
// All prefixes exist
return true;
}
};
// Solution class to find the longest word with all its prefixes present
class Solution {
public:
string completeString(vector<string>& nums) {
// Create a new Trie
Trie* obj = new Trie();
// Insert all words into the Trie
for (int i = 0; i < nums.size(); i++) {
obj->insert(nums[i]);
}
// Stores the longest valid word
string longest = "";
// Check each word to find the longest one where all prefixes exist
for (int i = 0; i < nums.size(); i++) {
if (obj->checkIfAllPrefixExists(nums[i])) {
if (nums[i].size() > longest.size()) {
longest = nums[i];
} else if (nums[i].size() == longest.size() && nums[i] < longest) {
// Lexicographically smaller word
longest = nums[i];
}
}
}
// Return result or "None"
return longest.empty() ? "None" : longest;
}
};
int main() {
int t;
cin >> t;
while (t--) {
Solution sol;
string testCase;
cin >> testCase;
cout << testCase << endl;
int n;
cin >> n;
vector<string> nums(n);
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
string ans = sol.completeString(nums);
cout << ans << endl;
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118
import java.util.*;
class Node {
// To store references to child nodes
Node[] links = new Node[26];
// Flag to indicate end of a word
boolean flag = false;
// Checks if the current character link exists
boolean containsKey(char ch) {
return links[ch - 'a'] != null;
}
// Returns the next node corresponding to the character
Node get(char ch) {
return links[ch - 'a'];
}
// Creates a link to the next node for the current character
void put(char ch, Node node) {
links[ch - 'a'] = node;
}
// Marks the end of a word
void setEnd() {
flag = true;
}
// Checks if the current node is the end of a word
boolean isEnd() {
return flag;
}
}
// Class representing the Trie (Prefix Tree) structure
class Trie {
// Root node of the Trie
Node root;
// Initializes the Trie
public Trie() {
root = new Node();
}
// Inserts a word into the Trie
public void insert(String word) {
Node node = root;
for (int i = 0; i < word.length(); i++) {
if (!node.containsKey(word.charAt(i))) {
node.put(word.charAt(i), new Node());
}
node = node.get(word.charAt(i));
}
// Marks the end of the inserted word
node.setEnd();
}
// Checks if all prefixes of the given word exist in the Trie
public boolean checkIfAllPrefixExists(String word) {
Node node = root;
for (int i = 0; i < word.length(); i++) {
if (node.containsKey(word.charAt(i))) {
node = node.get(word.charAt(i));
if (!node.isEnd()) {
// Prefix is incomplete, return false
return false;
}
} else {
// Return false if a character link is missing
return false;
}
}
// All prefixes exist
return true;
}
}
// Solution class to find the longest word with all its prefixes present
class Solution {
public String completeString(List<String> nums) {
Trie obj = new Trie();
// Insert all words into the Trie
for (String num : nums) {
obj.insert(num);
}
String longest = ""; // Stores the longest valid word
// Check each word to find the longest one where all prefixes exist
for (String num : nums) {
if (obj.checkIfAllPrefixExists(num)) {
if (num.length() > longest.length()) {
longest = num;
} else if (num.length() == longest.length() && num.compareTo(longest) < 0) {
longest = num; // Lexicographically smaller word
}
}
}
return longest.isEmpty() ? "None" : longest; // Return result or "None"
}
}
public class Main {
public static void main(String[] args) {
// Hardcoded test cases
List<String> testCase1 = Arrays.asList("n", "ni", "nin", "ninj" , "ninja" , "nil");
// Creating a solution instance
Solution sol = new Solution();
// Running test cases
System.out.println("Test Case 1: " + sol.completeString(testCase1)); // Expected: "ninja"
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101
class Node:
def __init__(self):
# To store references to child nodes
self.links = [None] * 26
# Flag to indicate end of a word
self.flag = False
# Checks if the current character link exists
def containsKey(self, ch):
return self.links[ord(ch) - ord('a')] is not None
# Returns the next node corresponding to the character
def get(self, ch):
return self.links[ord(ch) - ord('a')]
# Creates a link to the next node for the current character
def put(self, ch, node):
self.links[ord(ch) - ord('a')] = node
# Marks the end of a word
def setEnd(self):
self.flag = True
# Checks if the current node is the end of a word
def isEnd(self):
return self.flag
class Trie:
def __init__(self):
# Root node of the Trie
self.root = Node()
# Inserts a word into the Trie
def insert(self, word):
node = self.root
for char in word:
if not node.containsKey(char):
node.put(char, Node())
node = node.get(char)
# Marks the end of the inserted word
node.setEnd()
# Checks if all prefixes of the given word exist in the Trie
def checkIfAllPrefixExists(self, word):
node = self.root
for char in word:
if node.containsKey(char):
node = node.get(char)
if not node.isEnd():
# Prefix is incomplete, return false
return False
else:
# Return false if a character link is missing
return False
# All prefixes exist
return True
class Solution:
def completeString(self, nums):
# Create a new Trie
trie = Trie()
# Insert all words into the Trie
for word in nums:
trie.insert(word)
longest = "" # Stores the longest valid word
# Check each word to find the longest one where all prefixes exist
for word in nums:
if trie.checkIfAllPrefixExists(word):
if len(word) > len(longest):
longest = word
elif len(word) == len(longest) and word < longest:
longest = word # Lexicographically smaller word
# Return result or "None"
return longest if longest else "None"
if __name__ == "__main__":
# Hardcoded test cases
test_cases = [
("Test Case 1", ["n", "ni", "nin", "ninj" , "ninja" , "nil"]),
("Test Case 2", ["z", "zu", "zur", "zuri"]),
("Test Case 3", ["not", "none", "no", "on"]),
("Test Case 4", ["abcd", "ab", "a"]),
("Test Case 5", ["hello", "he", "hell", "hel", "h"])
]
for test_case, words in test_cases:
print(test_case)
print("Words:", words)
sol = Solution()
ans = sol.completeString(words)
print("Longest complete string with all prefixes:", ans)
print() # Blank line for better readability
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123
class Node {
constructor() {
// To store references to child nodes
this.links = Array(26).fill(null);
// Flag to indicate end of a word
this.flag = false;
}
// Checks if the current character link exists
containsKey(ch) {
return this.links[ch.charCodeAt(0) - 'a'.charCodeAt(0)] !== null;
}
// Returns the next node corresponding to the character
get(ch) {
return this.links[ch.charCodeAt(0) - 'a'.charCodeAt(0)];
}
// Creates a link to the next node for the current character
put(ch, node) {
this.links[ch.charCodeAt(0) - 'a'.charCodeAt(0)] = node;
}
// Marks the end of a word
setEnd() {
this.flag = true;
}
// Checks if the current node is the end of a word
isEnd() {
return this.flag;
}
}
class Trie {
constructor() {
// Root node of the Trie
this.root = new Node();
}
// Inserts a word into the Trie
insert(word) {
let node = this.root;
for (let i = 0; i < word.length; i++) {
if (!node.containsKey(word[i])) {
node.put(word[i], new Node());
}
node = node.get(word[i]);
}
// Marks the end of the inserted word
node.setEnd();
}
// Checks if all prefixes of the given word exist in the Trie
checkIfAllPrefixExists(word) {
let node = this.root;
for (let i = 0; i < word.length; i++) {
if (node.containsKey(word[i])) {
node = node.get(word[i]);
if (!node.isEnd()) {
return false; // Prefix is incomplete, return false
}
} else {
return false; // Return false if a character link is missing
}
}
return true; // All prefixes exist
}
}
class Solution {
completeString(nums) {
const obj = new Trie(); // Create a new Trie
// Insert all words into the Trie
for (let i = 0; i < nums.length; i++) {
obj.insert(nums[i]);
}
let longest = ""; // Stores the longest valid word
// Check each word to find the longest one where all prefixes exist
for (let i = 0; i < nums.length; i++) {
if (obj.checkIfAllPrefixExists(nums[i])) {
if (nums[i].length > longest.length) {
longest = nums[i];
} else if (nums[i].length === longest.length && nums[i] < longest) {
longest = nums[i]; // Lexicographically smaller word
}
}
}
return longest === "" ? "None" : longest;
}
}
// Example usage
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let input = [];
rl.on('line', function (line) {
input.push(line);
}).on('close', function () {
let t = parseInt(input[0]);
let idx = 1;
for (let i = 0; i < t; i++) {
console.log(input[idx++]); // Test case identifier
let n = parseInt(input[idx++]);
let nums = [];
for (let j = 0; j < n; j++) {
nums.push(input[idx++]);
}
let sol = new Solution();
console.log(sol.completeString(nums));
}
});