Largest BST in Binary Tree
Binary Search Trees
FAQs
Hard
- This problem taps into the core usage of the Binary Search Tree (BST) in software development
- Real-world applications of BSTs include database systems, such as MySQL, where managing and querying large amounts of data efficiently is a key requirement
- By ensuring certain subtrees maintain the properties of a BST, operations like searching, insertion, and deletion can be performed quicker, enhancing the overall performance
- This problem of identifying the largest BST in a binary tree echoes the optimization tasks often required in real-world applications
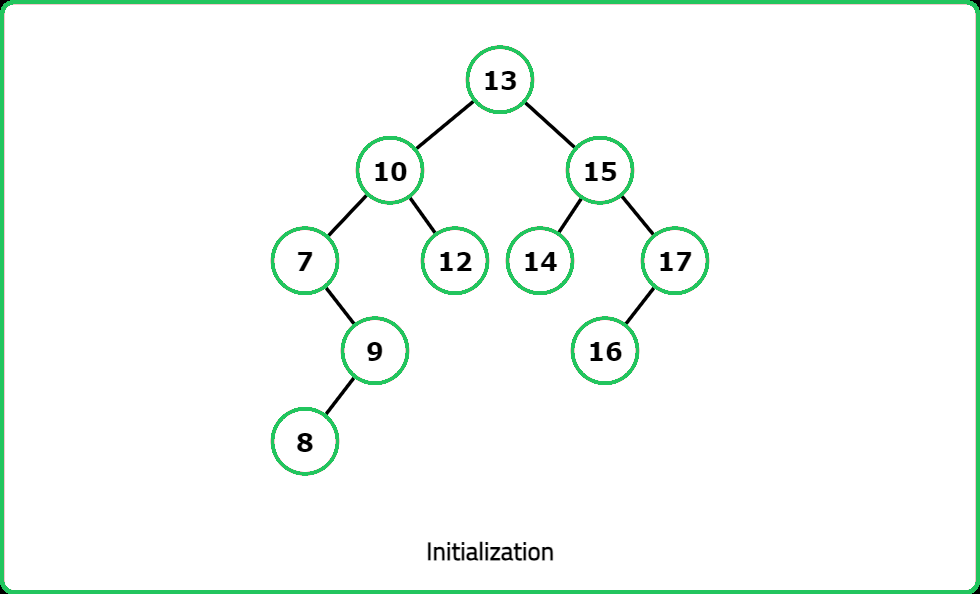
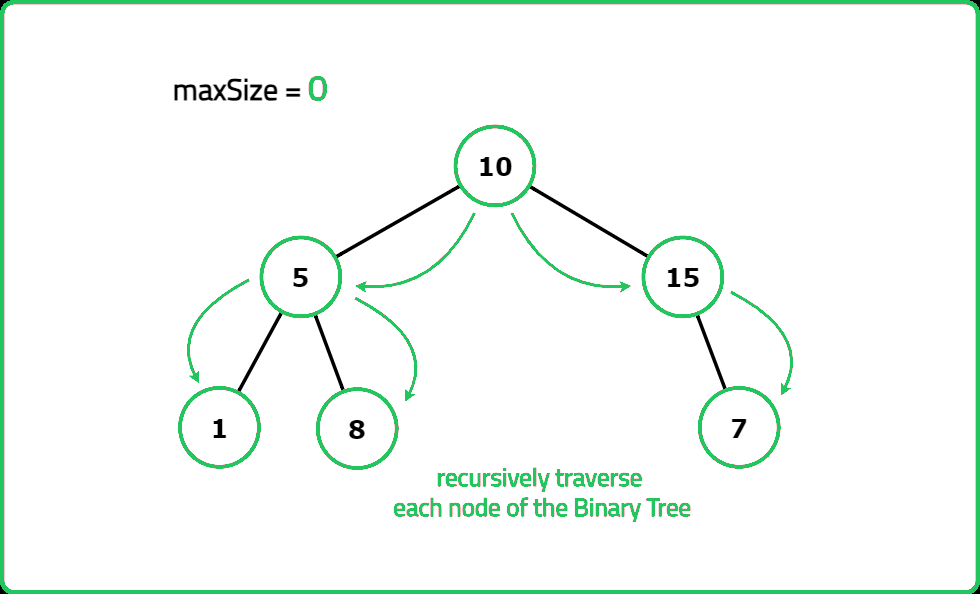
Given a root of Binary Tree, where the nodes have integer values. Return the size of the largest subtree of the binary tree which is also a BST.
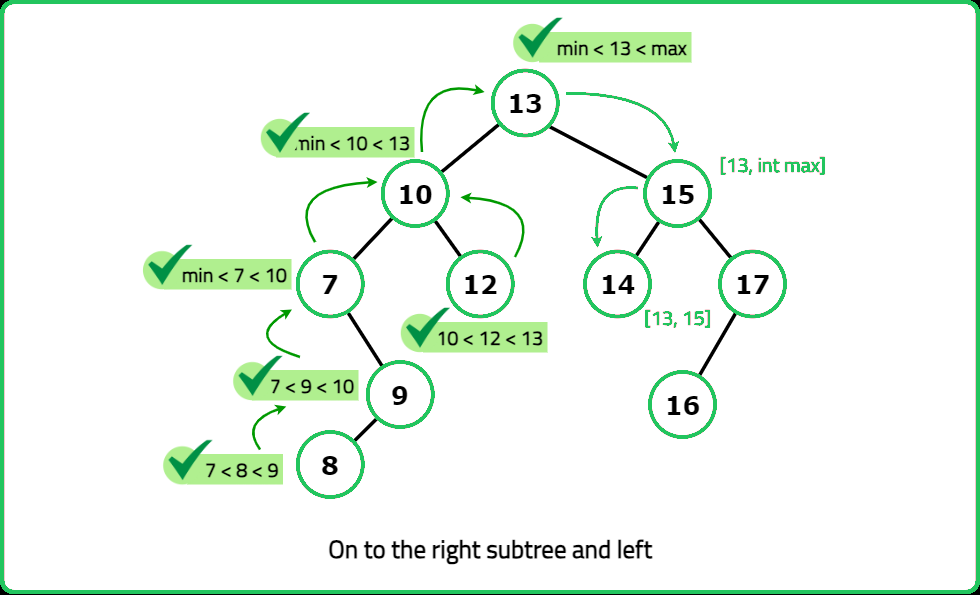
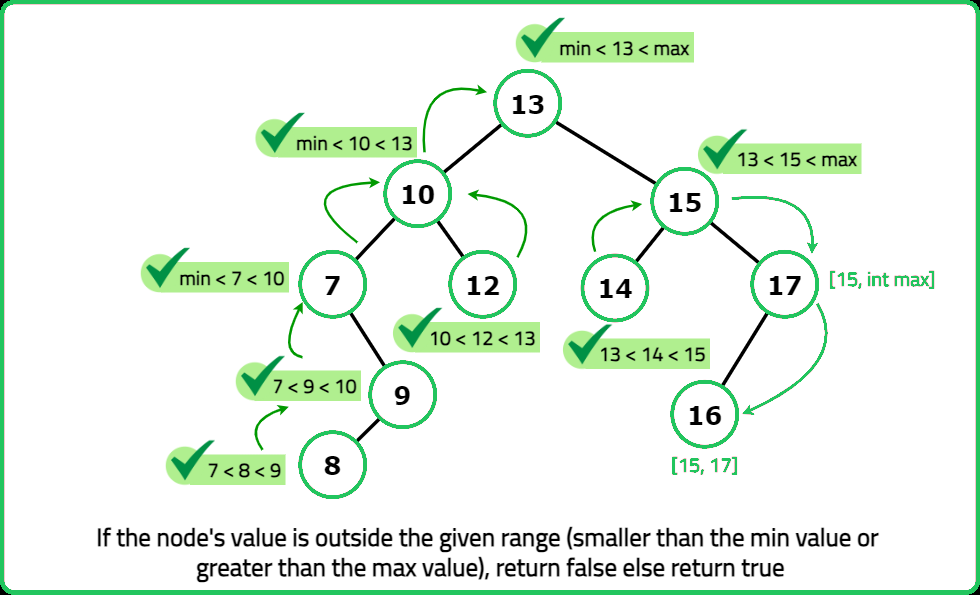
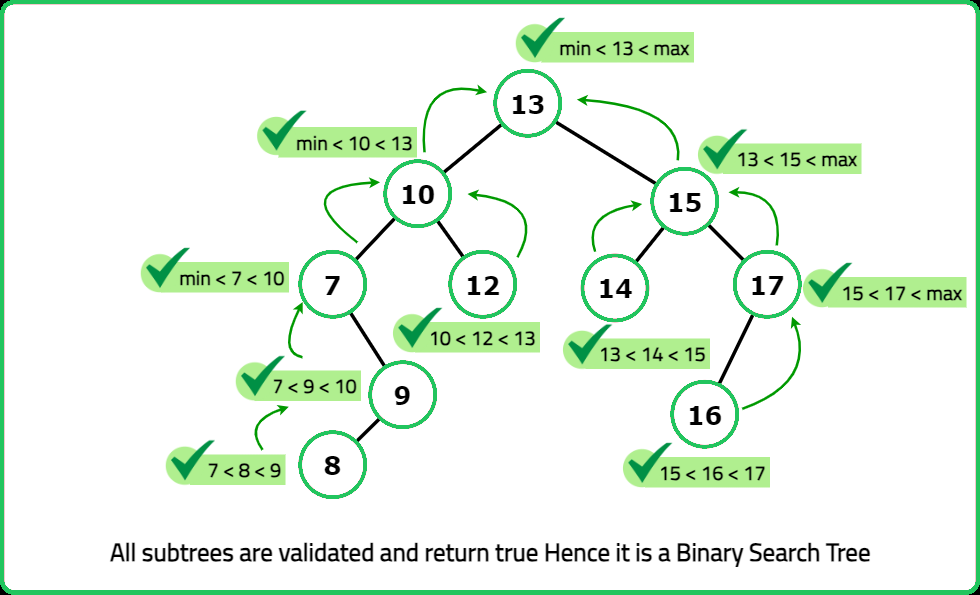
A binary search tree (BST) is a binary tree data structure which has the following properties.
- The left subtree of a node contains only nodes with data less than the nodeâs data.
- The right subtree of a node contains only nodes with data greater than the nodeâs data.
- Both the left and right subtrees must also be binary search trees.
Examples:
Input : root = [2, 1, 3]
Output : 3
Explanation : The given complete binary tree is a BST consisting of 3 nodes.

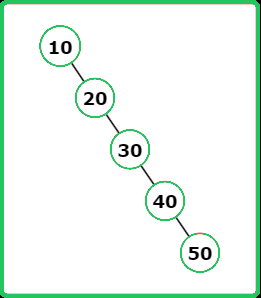
Input : root = [10, null, 20, null, 30, null, 40, null, 50]
Output : 5
Explanation : If we consider the node 10 as root node then it forms the largest BST.
Input : root = [3, 1, 4, null, null, 2]
Constraints
- 1 <= Number of Nodes <= 104
- 1 <= Node.val <= 105
Hints
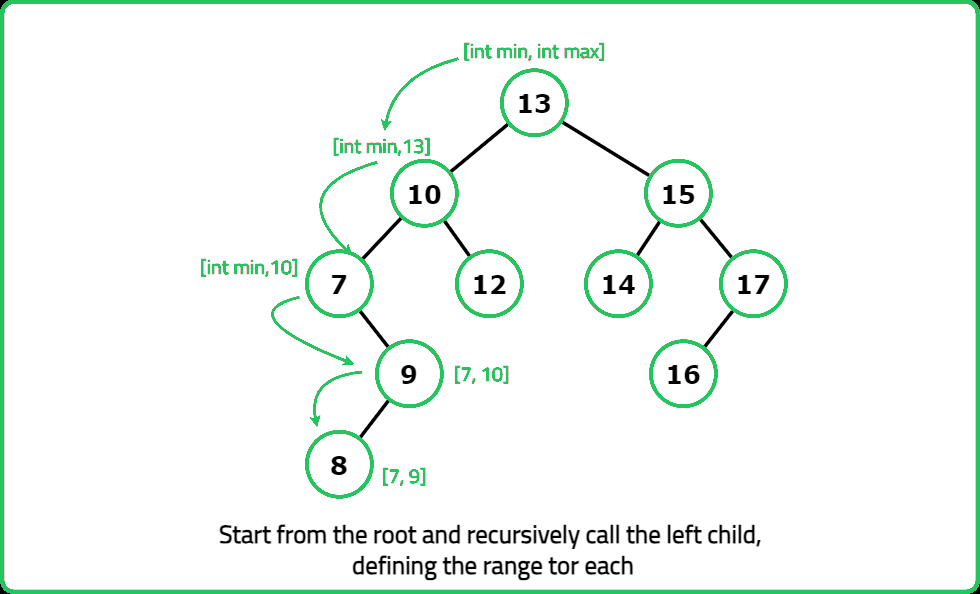
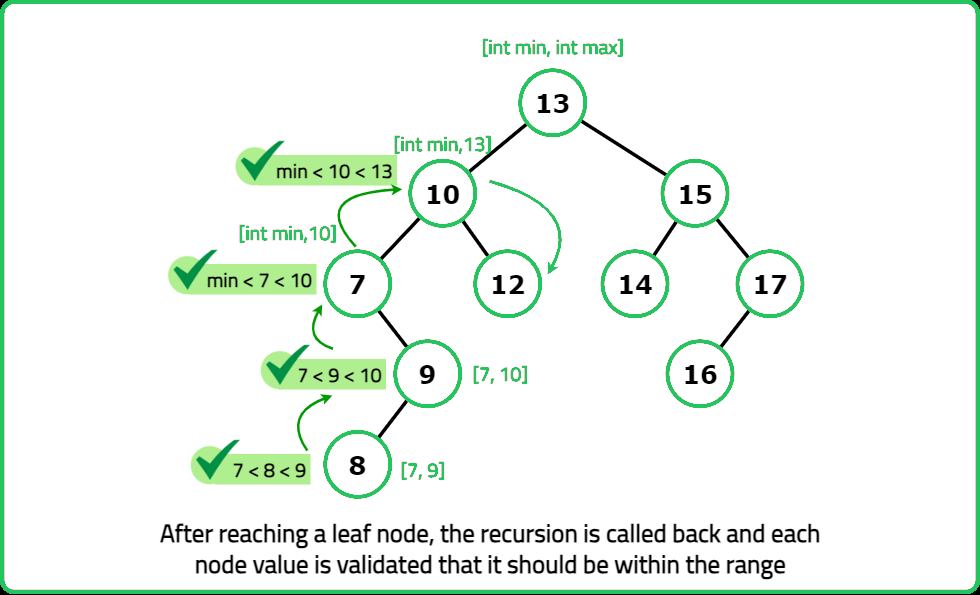
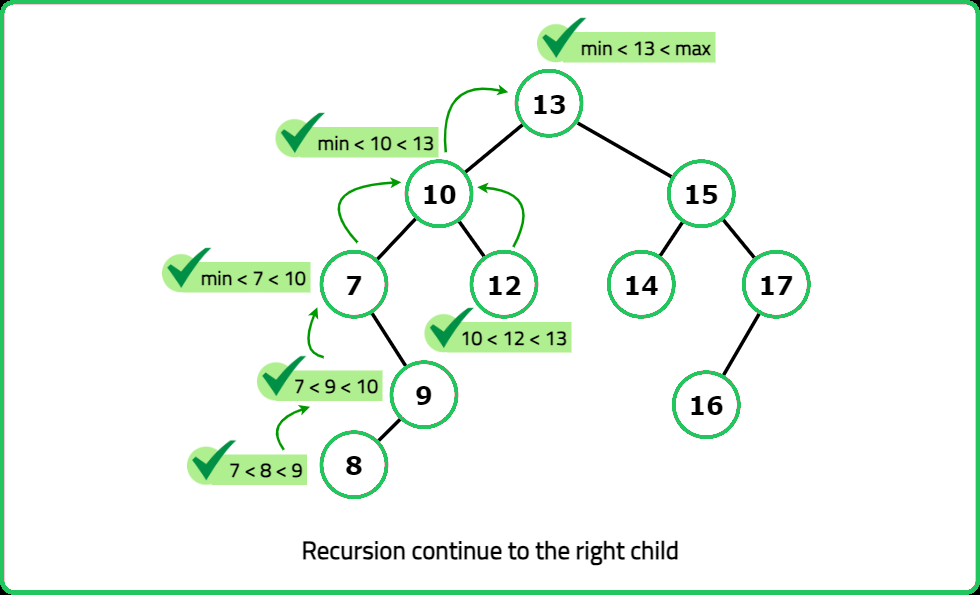
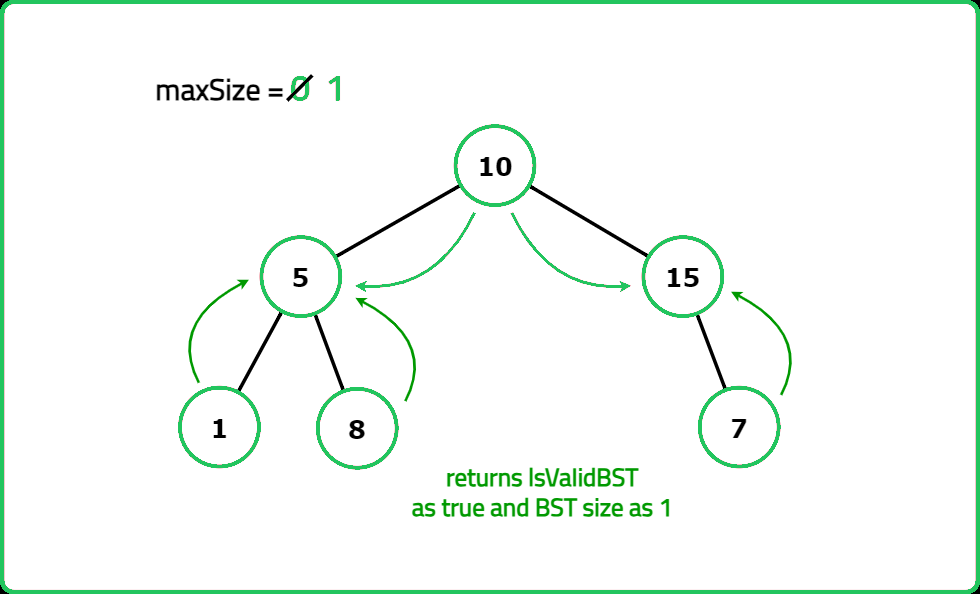
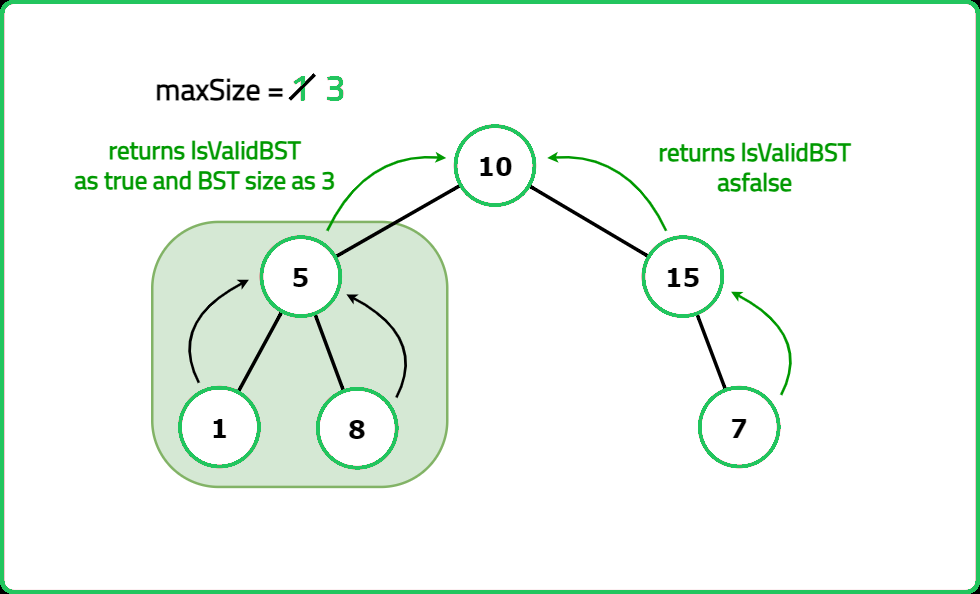
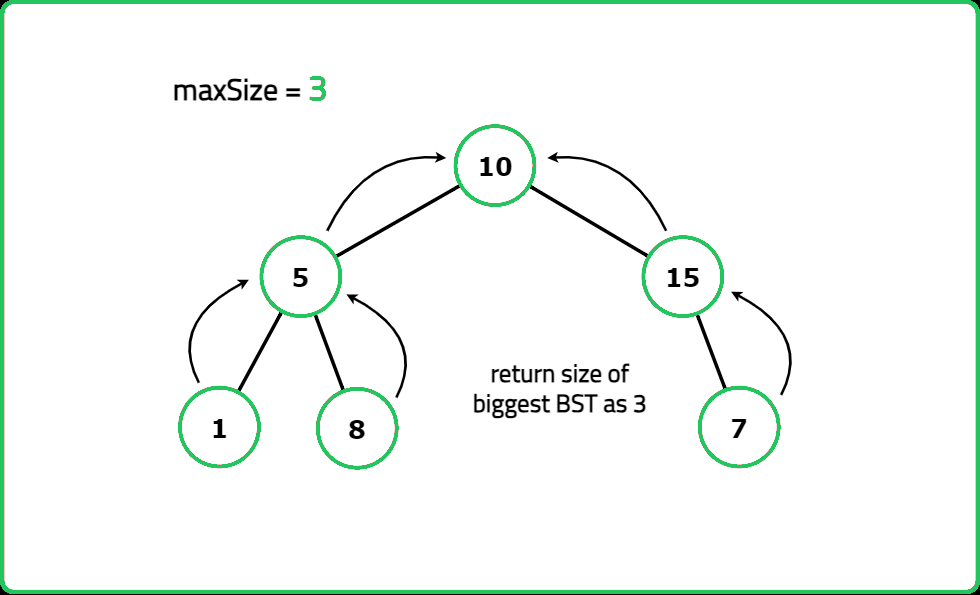
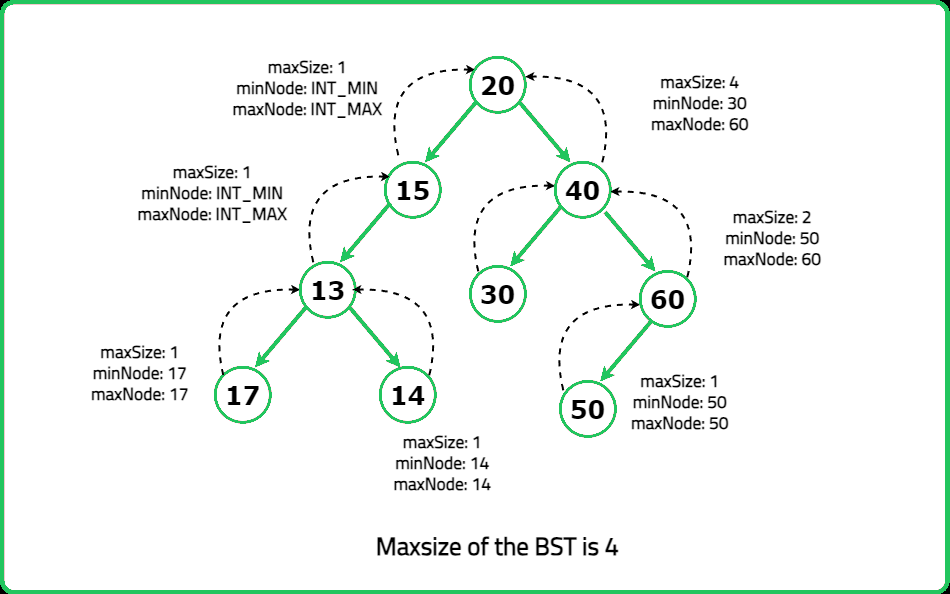
- "For each node: Recursively check left and right subtrees. Determine min, max, size of the largest BST subtree found. If the node satisfies BST conditions, update the maximum BST size."
- "Perform postorder traversal to check each subtree. Track min, max, size of the largest BST at each node. Return the largest BST size found. "
Company Tags
Wayfair
GE Healthcare
Cloudflare
Roche
Epic Systems
Texas Instruments
Snowflake
Bain & Company
Zomato
Philips Healthcare
Broadcom
OYO Rooms
Boston Consulting Group
Databricks
McKinsey & Company
Zoho
JPMorgan Chase
Visa
Twilio
Pinterest
Rockstar Games
Optum
Qualcomm
HashiCorp
Chewy
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe