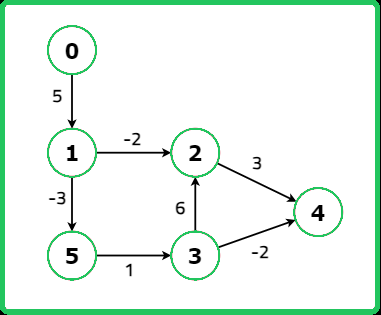
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to implement
Bellman Ford Algorithm */
vector<int> bellman_ford(int V, vector<vector<int>>& edges,
int S) {
// To store the distance
vector<int> dist(V, 1e9);
// Distane of source from itself is zero
dist[S] = 0;
// Repeat for V-1 times
for(int i=0; i<V-1; i++) {
// Iterate on all the edges
for(auto it : edges) {
int u = it[0]; // node 1
int v = it[1]; // node 2
int wt = it[2]; // edge weight
// Edge relaxation
if(dist[u] != 1e9 &&
dist[u] + wt < dist[v]) {
// Updating the known distance
dist[v] = dist[u] + wt;
}
}
}
/* An extra relaxation to check if the
graph consists of a negative cycle */
for(auto it : edges) {
int u = it[0]; // node 1
int v = it[1]; // node 2
int wt = it[2]; // edge weight
/* If edge relaxation is possible,
negative cycle exists */
if(dist[u] != 1e9 &&
dist[u] + wt < dist[v]) {
// Return {-1}
return {-1};
}
}
// Return the computed result
return dist;
}
};
int main() {
int V = 6, S = 0;
vector<vector<int>> edges = {
{3, 2, 6}, {5, 3, 1},
{0, 1, 5}, {1, 5, -3},
{1, 2, -2}, {3, 4, -2},
{2, 4, 3}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to implement
Bellman Ford Algorithm */
vector<int> ans = sol.bellman_ford(V, edges, S);
// Output
if(ans == vector<int>(1, -1))
cout << "The graph contains negative cycle.";
else{
cout << "The shortest distance from source is: ";
for(int i=0; i < V; i++) {
cout << ans[i] << " ";
}
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990
import java.util.*;
class Solution {
/* Function to implement
Bellman Ford Algorithm */
public int[] bellman_ford(int V,
ArrayList<ArrayList<Integer>> edges,
int S) {
// To store the distance
int[] dist = new int[V];
Arrays.fill(dist, (int) 1e9);
// Distance of source from itself is zero
dist[S] = 0;
// Repeat for V-1 times
for(int i = 0; i < V-1; i++) {
// Iterate on all the edges
for(ArrayList<Integer> it : edges) {
int u = it.get(0); // node 1
int v = it.get(1); // node 2
int wt = it.get(2); // edge weight
// Edge relaxation
if(dist[u] != 1e9 &&
dist[u] + wt < dist[v]) {
// Updating the known distance
dist[v] = dist[u] + wt;
}
}
}
/* An extra relaxation to check if the
graph consists of a negative cycle */
for(ArrayList<Integer> it : edges) {
int u = it.get(0); // node 1
int v = it.get(1); // node 2
int wt = it.get(2); // edge weight
/* If edge relaxation is possible,
negative cycle exists */
if(dist[u] != 1e9 &&
dist[u] + wt < dist[v]) {
// Return {-1}
return new int[]{-1};
}
}
// Return the computed result
return dist;
}
public static void main(String[] args) {
int V = 6, S = 0;
ArrayList<ArrayList<Integer>> edges = new ArrayList<>();
edges.add(new ArrayList<>(Arrays.asList(3, 2, 6)));
edges.add(new ArrayList<>(Arrays.asList(5, 3, 1)));
edges.add(new ArrayList<>(Arrays.asList(0, 1, 5)));
edges.add(new ArrayList<>(Arrays.asList(1, 5, -3)));
edges.add(new ArrayList<>(Arrays.asList(1, 2, -2)));
edges.add(new ArrayList<>(Arrays.asList(3, 4, -2)));
edges.add(new ArrayList<>(Arrays.asList(2, 4, 3)));
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to implement
Bellman Ford Algorithm */
int[] ans = sol.bellman_ford(V, edges, S);
// Output
if(ans.length == 1 && ans[0] == -1)
System.out.println("The graph contains negative cycle.");
else{
System.out.print("The shortest distance from source is: ");
for(int i = 0; i < V; i++) {
System.out.print(ans[i] + " ");
}
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
class Solution:
# Function to implement
# Bellman Ford Algorithm
def bellman_ford(self, V, edges, S):
# To store the distance
dist = [int(1e9)] * V
# Distance of source from itself is zero
dist[S] = 0
# Repeat for V-1 times
for _ in range(V-1):
# Iterate on all the edges
for u, v, wt in edges:
# Edge relaxation
if (dist[u] != int(1e9) and
dist[u] + wt < dist[v]):
# Updating the known distance
dist[v] = dist[u] + wt
# An extra relaxation to check if the
# graph consists of a negative cycle
for u, v, wt in edges:
# If edge relaxation is possible,
# negative cycle exists
if (dist[u] != int(1e9) and
dist[u] + wt < dist[v]):
# Return [-1]
return [-1]
# Return the computed result
return dist
if __name__ == "__main__":
V, S = 6, 0
edges = [
[3, 2, 6], [5, 3, 1],
[0, 1, 5], [1, 5, -3],
[1, 2, -2], [3, 4, -2],
[2, 4, 3]
]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to implement
# Bellman Ford Algorithm
ans = sol.bellman_ford(V, edges, S)
# Output
if ans == [-1]:
print("The graph contains negative cycle.")
else:
print("The shortest distance from source is: ", end=" ")
for d in ans:
print(d, end=" ")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677
class Solution {
/* Function to implement
Bellman Ford Algorithm */
bellman_ford(V, edges, S) {
// To store the distance
let dist = new Array(V).fill(1e9);
// Distance of source from itself is zero
dist[S] = 0;
// Repeat for V-1 times
for (let i = 0; i < V-1; i++) {
// Iterate on all the edges
for (let it of edges) {
let u = it[0]; // node 1
let v = it[1]; // node 2
let wt = it[2]; // edge weight
// Edge relaxation
if (dist[u] != 1e9 && dist[u] + wt < dist[v]) {
// Updating the known distance
dist[v] = dist[u] + wt;
}
}
}
/* An extra relaxation to check if the
graph consists of a negative cycle */
for (let it of edges) {
let u = it[0]; // node 1
let v = it[1]; // node 2
let wt = it[2]; // edge weight
/* If edge relaxation is possible,
negative cycle exists */
if (dist[u] != 1e9 && dist[u] + wt < dist[v]) {
// Return [-1]
return [-1];
}
}
// Return the computed result
return dist;
}
}
// Main function
let V = 6, S = 0;
let edges = [
[3, 2, 6], [5, 3, 1],
[0, 1, 5], [1, 5, -3],
[1, 2, -2], [3, 4, -2],
[2, 4, 3]
];
/* Creating an instance of
Solution class */
let sol = new Solution();
/* Function call to implement
Bellman Ford Algorithm */
let ans = sol.bellman_ford(V, edges, S);
// Output
if (ans.length === 1 && ans[0] === -1)
console.log("The graph contains negative cycle.");
else {
console.log("The shortest distance from source is: ", ans.join(" "));
}