Coin change II

As the question is asking for the total number of ways in which the coins can be summed up to give the target. So, recusion can be used to solve this problem.

Steps to form the recusive solution:

Express the problem in terms of indexes:We are given ‘n’ coins, where 'n' is the size of the array. Their denomination value is given by the array ‘arr’. So clearly one parameter will be ‘ind’, i.e index up to which the array items are being considered. There is one more parameter, the given target value 'T' which we want to achieve so that while generating subsequences, we can decide whether we want to include a particular coin or not.

So, initially, we need to find f(n-1, T) where T is the initial target given to us in the question. f(n-1, T) gives the total number of ways to form the target T by considering coins from index 0 to index n-1 of the arr array.

Try out all possible choices at a given index:We need to generate all the subsequences. So, use the pick/non-pick technique. There are two choices:

Exclude the current coin from the subsequence:First try to find a subsequence without considering the current index coin. If the current coin is excluded, the target sum will not be affected. So call the recursive function f(ind-1,T) to find the remaining answer.

Include the current element in the subsequence: Try to find a subsequence by considering the current icoin. As the coin has been included, the target sum will be updated to T-arr[ind].

Now here is the catch, as there is an unlimited supply of coins, we want to again form a solution with the same coin value. So we will not recursively call for f(ind-1, T-arr[ind]) rather we will stay at that index only and call for f(find, T-arr[ind]) to find the answer.

Note: Consider the current coin only when its denomination value (arr[ind]) is less than or equal to the target T.

f(ind, T){
    notTake = 0 + f(ind-1, T)
    take = 0
    if(arr[ind] <= T)
         take = f(ind, T-arr[ind])
}

Return the sum of 'take' and 'notTake':As we have to return the total number of ways we can form the target, we will return the sum of 'notTake' and 'take' as our answer.

f(ind, T){
    notTake = 0 + f(ind-1, T)
    take = 0
    if(arr[ind] <= T)
         take = f(ind, T-arr[ind])
    return take + notTake
}

Base Cases:If ind==0, it means we are at the first item so we have only one coin denomination, therefore the following two cases can arise:
When target 'T' is divisible by arr[0]. In such case where the target is divisible by the coin element value, return 1 as we will be able to form the target.
T is not divisible by arr[0]. In all other cases, we will not be able to form the target, so we will return 0.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to count the number of ways 
    to make change for a given target sum*/
    int func(vector<int>& arr, int ind, int T) {
        // Base case: if we're at the first element
        if (ind == 0) {
            /* Check if the target sum is 
            divisible by the first element*/
            return (T % arr[0] == 0);
        }
        
        /* Calculate the number of ways 
        without taking the current element*/
        int notTaken = func(arr, ind - 1, T);
    
        /* Calculate the number of ways
        by taking the current element*/
        int taken = 0;
        if (arr[ind] <= T)
            taken = func(arr, ind, T - arr[ind]);
        
        // Return the sum of ways
        return notTaken + taken;
   }
public:
    /* Function to count the number of 
    ways to make change for the target sum*/
    int count(vector<int>& coins, int N, int amount) {
    
        // Call the utility function to calculate the answer
        return func(coins, N - 1, amount);
    }
};

int main() {
   vector<int> coins = {1, 2, 3};
    int amount = 4;
    int N = coins.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.count(coins, N, amount) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    /* Function to count the number of ways 
    to make change for a given target sum*/
    private int func(int[] arr, int ind, int T) {
        // Base case: if we're at the first element
        if (ind == 0) {
            /* Check if the target sum is 
            divisible by the first element*/
            return (T % arr[0] == 0) ? 1 : 0;
        }

        /* Calculate the number of ways 
        without taking the current element*/
        int notTaken = func(arr, ind - 1, T);

        /* Calculate the number of ways
        by taking the current element*/
        int taken = 0;
        if (arr[ind] <= T)
            taken = func(arr, ind, T - arr[ind]);

        // Return the sum of ways
        return notTaken + taken;
    }

    /* Function to count the number of 
    ways to make change for the target sum*/
    public int count(int[] coins, int N, int amount) {

        // Call the utility function to calculate answer
        return func(coins, N - 1, amount);
    }
}

public class Main {
    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int amount = 4;
        int N = coins.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.count(coins, N, amount));
    }
}
class Solution:
    """ Function to count the number of ways 
    to make change for a given target sum"""
    def func(self, arr, ind, T):
        # Base case: if we're at the first element
        if ind == 0:
            """ Check if the target sum is
            divisible by the first element"""
            return 1 if T % arr[0] == 0 else 0

        """ Calculate the number of ways 
        without taking the current element"""
        notTaken = self.func(arr, ind - 1, T)

        """ Calculate the number of ways
        by taking the current element"""
        taken = 0
        if arr[ind] <= T:
            taken = self.func(arr, ind, T - arr[ind])

        # Return the sum of ways 
        return notTaken + taken

    """ Function to count the number of ways
    to make change for the target sum"""
    def count(self, coins, N, amount):
        
        # Call the utility function to calculate the answer
        return self.func(coins, N - 1, amount)

if __name__ == "__main__":
    coins = [1, 2, 3]
    amount = 4
    N = len(coins)

    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The total number of ways is", sol.count(coins, N, amount))
class Solution {
    /* Function to count the number of ways 
    to make change for a given target sum*/
    func(arr, ind, T) {
        // Base case: if we're at the first element
        if (ind === 0) {
            /* Check if the target sum is
            divisible by the first element*/
            return (T % arr[0] === 0) ? 1 : 0;
        }

        /* Calculate the number of ways
        without taking the current element*/
        const notTaken = this.func(arr, ind - 1, T);

        /* Calculate the number of ways 
        by taking the current element*/
        let taken = 0;
        if (arr[ind] <= T)
            taken = this.func(arr, ind, T - arr[ind]);

        // Return the sum of ways
        return notTaken + taken;
    }

    /* Function to count the number of ways
    to make change for the target sum */
    count(coins, N, amount) {

        // Call the utility function to calculate  answer
        return this.func(coins, N - 1, amount);
    }
}

const coins = [1, 2, 3];
const amount = 4;
const N = coins.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.count(coins, N, amount));

Complexity Analysis:

Time Complexity:O(2^N), as there are N coints can each one of them has 2 options.

Space Complexity:O(N), the depth of the recursion stack can be N at max.

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

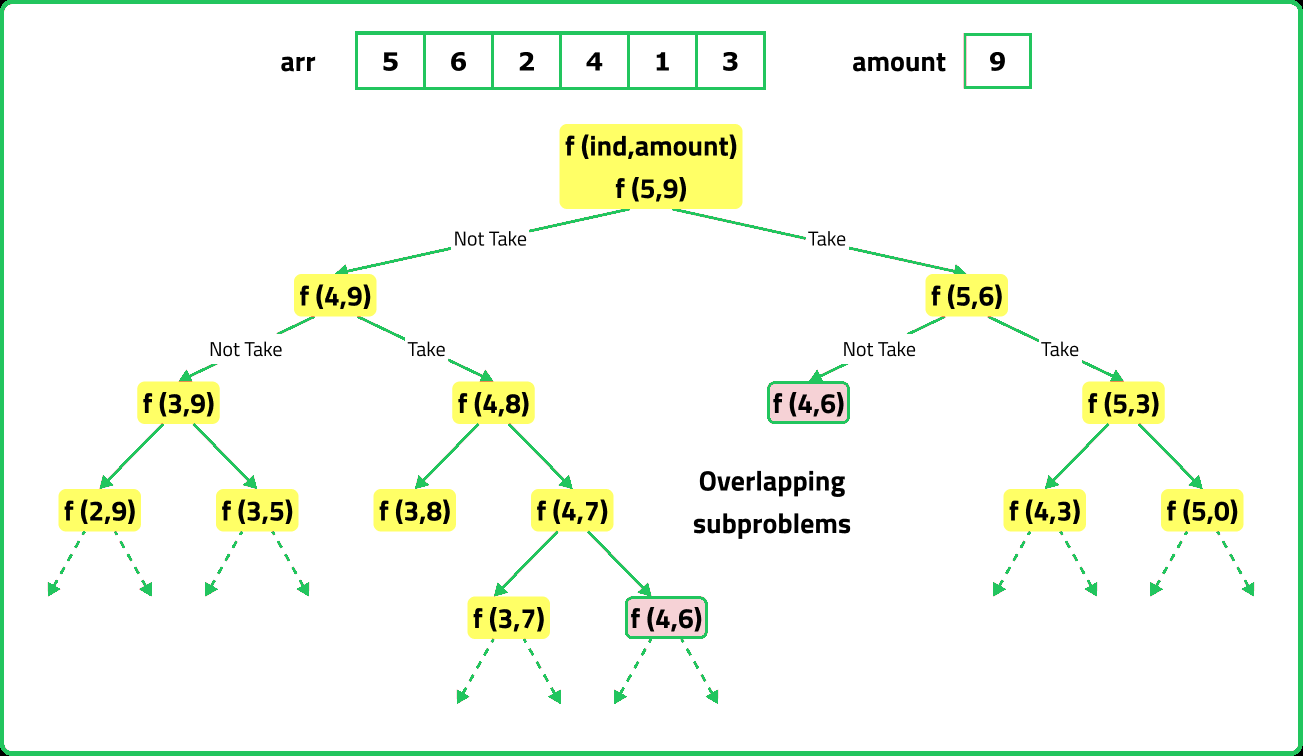
In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'target' only values between 0 to target. Therefore, we need 2D dp array.

The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to count the number of ways 
    to make change for a given target sum*/
    int func(vector<int>& arr, int ind, int T, vector<vector<int>>& dp) {
        // Base case: if we're at the first element
        if (ind == 0) {
            /* Check if the target sum is 
            divisible by the first element*/
            return (T % arr[0] == 0);
        }
    
        /* If the result for this index and target 
        sum is already calculated, return it*/
        if (dp[ind][T] != -1)
            return dp[ind][T];
        
        /* Calculate the number of ways 
        without taking the current element*/
        int notTaken = func(arr, ind - 1, T, dp);
    
        /* Calculate the number of ways
        by taking the current element*/
        int taken = 0;
        if (arr[ind] <= T)
            taken = func(arr, ind, T - arr[ind], dp);
        
        /* Store the sum of ways in 
        the DP table and return it*/
        return dp[ind][T] = notTaken + taken;
   }
public:
    /* Function to count the number of 
    ways to make change for the target sum*/
    int count(vector<int>& coins, int N, int amount) {
        vector<vector<int>> dp(N, vector<int>(amount + 1, -1)); 
    
        // Call the utility function to calculate the answer
        return func(coins, N - 1, amount, dp);
    }
};

int main() {
   vector<int> coins = {1, 2, 3};
    int amount = 4;
    int N = coins.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.count(coins, N, amount) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    /* Function to count the number of ways 
    to make change for a given target sum*/
    private int func(int[] arr, int ind, int T, int[][] dp) {
        // Base case: if we're at the first element
        if (ind == 0) {
            /* Check if the target sum is 
            divisible by the first element*/
            return (T % arr[0] == 0) ? 1 : 0;
        }

        /* If the result for this index and target 
        sum is already calculated, return it*/
        if (dp[ind][T] != -1)
            return dp[ind][T];

        /* Calculate the number of ways 
        without taking the current element*/
        int notTaken = func(arr, ind - 1, T, dp);

        /* Calculate the number of ways
        by taking the current element*/
        int taken = 0;
        if (arr[ind] <= T)
            taken = func(arr, ind, T - arr[ind], dp);

        /* Store the sum of ways in 
        the DP table and return it*/
        return dp[ind][T] = notTaken + taken;
    }

    /* Function to count the number of 
    ways to make change for the target sum*/
    public int count(int[] coins, int N, int amount) {
        int[][] dp = new int[N][amount + 1];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }

        // Call the utility function to calculate answer
        return func(coins, N - 1, amount, dp);
    }
}

public class Main {
    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int amount = 4;
        int N = coins.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.count(coins, N, amount));
    }
}
class Solution:
    """ Function to count the number of ways 
    to make change for a given target sum"""
    def func(self, arr, ind, T, dp):
        # Base case: if we're at the first element
        if ind == 0:
            """ Check if the target sum is
            divisible by the first element"""
            return 1 if T % arr[0] == 0 else 0

        """ If the result for this index and target
        sum is already calculated, return it"""
        if dp[ind][T] != -1:
            return dp[ind][T]

        """ Calculate the number of ways 
        without taking the current element"""
        notTaken = self.func(arr, ind - 1, T, dp)

        """ Calculate the number of ways
        by taking the current element"""
        taken = 0
        if arr[ind] <= T:
            taken = self.func(arr, ind, T - arr[ind], dp)

        """ Store the sum of ways in 
        the DP table and return it"""
        dp[ind][T] = notTaken + taken
        return dp[ind][T]

    """ Function to count the number of ways
    to make change for the target sum"""
    def count(self, coins, N, amount):
        dp = [[-1] * (amount + 1) for _ in range(N)]
        
        # Call the utility function to calculate the answer
        return self.func(coins, N - 1, amount, dp)

if __name__ == "__main__":
    coins = [1, 2, 3]
    amount = 4
    N = len(coins)

    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The total number of ways is", sol.count(coins, N, amount))
class Solution {
    /* Function to count the number of ways 
    to make change for a given target sum*/
    func(arr, ind, T, dp) {
        // Base case: if we're at the first element
        if (ind === 0) {
            /* Check if the target sum is
            divisible by the first element*/
            return (T % arr[0] === 0) ? 1 : 0;
        }

        /* If the result for this index and target
        sum is already calculated, return it*/
        if (dp[ind][T] !== -1)
            return dp[ind][T];

        /* Calculate the number of ways
        without taking the current element*/
        const notTaken = this.func(arr, ind - 1, T, dp);

        /* Calculate the number of ways 
        by taking the current element*/
        let taken = 0;
        if (arr[ind] <= T)
            taken = this.func(arr, ind, T - arr[ind], dp);

        /* Store the sum of ways in
        the DP table and return it*/
        dp[ind][T] = notTaken + taken;
        return dp[ind][T];
    }

    /* Function to count the number of ways
    to make change for the target sum */
    count(coins, N, amount) {
        const dp = Array.from({ length: N }, () => Array(amount + 1).fill(-1));

        // Call the utility function to calculate  answer
        return this.func(coins, N - 1, amount, dp);
    }
}

const coins = [1, 2, 3];
const amount = 4;
const N = coins.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.count(coins, N, amount));

Complexity Analysis:

Time Complexity:O(N*Target), as there are N*Target states therefore at max ‘N*Target’ new problems will be solved.

Space Complexity:O(N*Target) + O(N), the stack space will be O(N) and a 2D array of size N*T is used.

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n) and including 0 its n, where n is the size of array, for 'target' can have any values between 0 to 'target'. So we need a 2D dp array. Set its type as int and initialize it as 0.
Setting Base Cases in the Array: In the recursive code, our base condition was when 'ind' == 0, it means we were considering the first element. So for 'ind' == 0, if T%arr[0] ==0, initialize the dp array to 1 else initialize it to 0.
Iterative Computation Using Loops: As we are done for the first row(ind = 0) in the base case, so ‘ind’ variable will move from 1 to n-1, whereas ‘target’ variable will move from 0 to 'T'(target). Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.
Returning the answer: At last dp[n-1][target] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    /* Function to count the number of 
    ways to make change for the target sum*/
    int count(vector<int>& coins, int N, int amount) {
    
        vector<vector<int>> dp(N, vector<int>(amount + 1, 0)); 

        // Initializing base condition
        for (int i = 0; i <= amount; i++) {
            if (i % coins[0] == 0)
                dp[0][i] = 1;
            /* Else condition is automatically fulfilled,
            as dp array is initialized to zero*/
        }

        for (int ind = 1; ind < N; ind++) {
            for (int target = 0; target <= amount; target++) {
                int notTaken = dp[ind - 1][target];

                int taken = 0;
                if (coins[ind] <= target)
                    taken = dp[ind][target - coins[ind]];

                dp[ind][target] = notTaken + taken;
            }
        }
        //Return the result
        return dp[N - 1][amount];
    }
};

int main() {
   vector<int> coins = {1, 2, 3};
    int amount = 4;
    int N = coins.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.count(coins, N, amount) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    /* Function to count the number of 
    ways to make change for the target sum*/
    public int count(int[] coins, int N, int amount) {
        int[][] dp = new int[N][amount + 1];

        // Initializing base condition
        for (int i = 0; i <= amount; i++) {
            if (i % coins[0] == 0)
                dp[0][i] = 1;
            // Else condition is automatically fulfilled,
            // as dp array is initialized to zero
        }

        for (int ind = 1; ind < N; ind++) {
            for (int target = 0; target <= amount; target++) {
                int notTaken = dp[ind - 1][target];

                int taken = 0;
                if (coins[ind] <= target)
                    taken = dp[ind][target - coins[ind]];

                dp[ind][target] = notTaken + taken;
            }
        }
        // Return the result
        return dp[N - 1][amount];
    }
}

public class Main {
    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int amount = 4;
        int N = coins.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.count(coins, N, amount));
    }
}
class Solution:
    """ Function to count the number of 
    ways to make change for the target sum"""
    def count(self, coins, N, amount):
        dp = [[0] * (amount + 1) for _ in range(N)]

        # Initializing base condition
        for i in range(amount + 1):
            if i % coins[0] == 0:
                dp[0][i] = 1
            """ Else condition is automatically fulfilled,
            as dp array is initialized to zero"""

        for ind in range(1, N):
            for target in range(amount + 1):
                notTaken = dp[ind - 1][target]

                taken = 0
                if coins[ind] <= target:
                    taken = dp[ind][target - coins[ind]]

                dp[ind][target] = notTaken + taken

        # Return the result
        return dp[N - 1][amount]

if __name__ == "__main__":
    coins = [1, 2, 3]
    amount = 4
    N = len(coins)

    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The total number of ways is", sol.count(coins, N, amount))
class Solution {
    /* Function to count the number of 
    ways to make change for the target sum */
    count(coins, N, amount) {
        const dp = Array.from({ length: N }, () => Array(amount + 1).fill(0));

        // Initializing base condition
        for (let i = 0; i <= amount; i++) {
            if (i % coins[0] === 0)
                dp[0][i] = 1;
            /* Else condition is automatically fulfilled,
            as dp array is initialized to zero*/
        }

        for (let ind = 1; ind < N; ind++) {
            for (let target = 0; target <= amount; target++) {
                const notTaken = dp[ind - 1][target];

                let taken = 0;
                if (coins[ind] <= target)
                    taken = dp[ind][target - coins[ind]];

                dp[ind][target] = notTaken + taken;
            }
        }
        // Return the result
        return dp[N - 1][amount];
    }
}

const coins = [1, 2, 3];
const amount = 4;
const N = coins.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.count(coins, N, amount));

Complexity Analysis:

Time Complexity:O(N*Target), as there are N*Target states therefore at max ‘N*Target’ new problems will be solved.

Space Complexity:O(N*Target), as a 2D array of size N*Target is used.

If we observe the relation obtained in the tabulation approach, dp[ind][target] = dp[ind-1][target] + dp[ind-1][target-arr[ind]]. We see that to calculate a value of a cell of the dp array, only the previous row values (say prev) are need. So, we don’t need to store an entire array for that. Hence we can space optimize it.

Note: We first need to initialize the first row as we had done in the tabulation approach.

Steps to consider for space optimization:

Declare two arrays to store results of subproblems 'prev' and 'cur'. Initialize the 'prev' array for the first element of the array, as we did in the tabulation approach, for handling the base case.
Fill the 'cur' array for present row using nested loops and the same logic discussed in tabulation. If the current element is less than or equal to the target, calculate 'take'.
As, the problem is asking for total ways, store the sum of 'take' and 'not take' in the 'cur' array.
Update 'prev' with 'cur' for the next iteration and at last get the minimum number of coins needed for the target sum stored in 'prev[Target]'.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    /* Function to count the number of 
    ways to make change for the target sum*/
    int count(vector<int>& coins, int N, int amount) {
        // Initialize a vector to store previous DP state
        vector<int> prev(amount + 1, 0);  

        // Initialize base condition
        for (int i = 0; i <= amount; i++) {
            /* There is one way to make change
            for multiples of the first coin*/
            if (i % coins[0] == 0)
                prev[i] = 1;  
            /* Else condition is automatically fulfilled,
            as the prev vector is initialized to zero*/
        }

        for (int ind = 1; ind < N; ind++) {
            // Initialized a vector to store current DP state
            vector<int> cur(amount + 1, 0);  
            for (int target = 0; target <= amount; target++) {
                
                // Number of ways without taking current coin
                int notTaken = prev[target];  

                int taken = 0;
                if (coins[ind] <= target)
                    // Number of ways by taking current coin
                    taken = cur[target - coins[ind]];  
                
                // Total number of ways for current target
                cur[target] = notTaken + taken;  
            }
            /* Update the previous DP state with 
            the current state for the next coin*/
            prev = cur;  
        }
        /* Return the total number of ways
        to make change for the target*/
        return prev[amount];  
    }
};

int main() {
   vector<int> coins = {1, 2, 3};
    int amount = 4;
    int N = coins.size(); 
    
    //Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The total number of ways is " << sol.count(coins, N, amount) << endl;

    return 0; 
}

import java.util.*;

class Solution {
    /* Function to count the number of 
    ways to make change for the target sum */
    public int count(int[] coins, int N, int amount) {
        // Initialize a vector to store previous DP state
        int[] prev = new int[amount + 1];  

        // Initialize base condition
        for (int i = 0; i <= amount; i++) {
            /* There is one way to make change
            for multiples of the first coin */
            if (i % coins[0] == 0)
                prev[i] = 1;  
            /* Else condition is automatically fulfilled,
            as the prev array is initialized to zero*/
        }

        for (int ind = 1; ind < N; ind++) {
            // Initialized an array to store current DP state
            int[] cur = new int[amount + 1];  
            for (int target = 0; target <= amount; target++) {
                
                // Number of ways without taking current coin
                int notTaken = prev[target];  

                int taken = 0;
                if (coins[ind] <= target)
                    // Number of ways by taking current coin
                    taken = cur[target - coins[ind]];  
                
                // Total number of ways for current target
                cur[target] = notTaken + taken;  
            }
            /* Update the previous DP state with 
            the current state for the next coin */
            prev = cur;  
        }
        /* Return the total number of ways
        to make change for the target */
        return prev[amount];  
    }
}

public class Main {
    public static void main(String[] args) {
        int[] coins = {1, 2, 3};
        int amount = 4;
        int N = coins.length; 
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The total number of ways is " + sol.count(coins, N, amount));
    }
}
class Solution:
    """ Function to count the number of 
    ways to make change for the target sum"""
    def count(self, coins, N, amount):
        # Initialize a list to store previous DP state
        prev = [0] * (amount + 1)  

        # Initialize base condition
        for i in range(amount + 1):
            """ There is one way to make change 
            for multiples of the first coin"""
            if i % coins[0] == 0:
                prev[i] = 1  
            """ Else condition is automatically fulfilled,
            as the prev list is initialized to zero"""

        for ind in range(1, N):
            # Initialize a list to store current DP state
            cur = [0] * (amount + 1)  
            for target in range(amount + 1):
                
                # Number of ways without taking current coin
                notTaken = prev[target]  

                taken = 0
                if coins[ind] <= target:
                    # Number of ways by taking current coin
                    taken = cur[target - coins[ind]]  
                
                # Total number of ways for current target
                cur[target] = notTaken + taken  
            
            """ Update the previous DP state with 
            the current state for the next coin"""
            prev = cur  
        
        """ Return the total number of ways 
        to make change for the target"""
        return prev[amount]  

if __name__ == "__main__":
    coins = [1, 2, 3]
    amount = 4
    N = len(coins)
    
    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The total number of ways is", sol.count(coins, N, amount))
class Solution {
    /* Function to count the number of 
    ways to make change for the target sum */
    count(coins, N, amount) {
        // Initialize an array to store previous DP state
        let prev = new Array(amount + 1).fill(0);  

        // Initialize base condition
        for (let i = 0; i <= amount; i++) {
            /* There is one way to make change
            for multiples of the first coin*/
            if (i % coins[0] === 0)
                prev[i] = 1;  
            /* Else condition is automatically fulfilled,
            as the prev array is initialized to zero*/
        }

        for (let ind = 1; ind < N; ind++) {
            // Initialize an array to store current DP state
            let cur = new Array(amount + 1).fill(0);  
            for (let target = 0; target <= amount; target++) {
                
                // Number of ways without taking current coin
                let notTaken = prev[target];  

                let taken = 0;
                if (coins[ind] <= target)
                    // Number of ways by taking current coin
                    taken = cur[target - coins[ind]];  
                
                // Total number of ways for current target
                cur[target] = notTaken + taken;  
            }
            /* Update the previous DP state with 
            the current state for the next coin*/
            prev = cur;  
        }
        /* Return the total number of ways 
        to make change for the target*/
        return prev[amount];  
    }
}

const coins = [1, 2, 3];
const amount = 4;
const N = coins.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The total number of ways is " + sol.count(coins, N, amount));

Complexity Analysis:

Time Complexity:O(N*Target), as there are N*Target states therefore at max ‘N*Target’ new problems will be solved.

Space Complexity:O(Target), as a 2D array of size (Target+1) is used.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form the recusive solution:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Steps to consider for space optimization:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code