Power Set Bit Manipulation

Bit Manipulation Problems Medium

The concept of generating all possible subsets of a set (also known as power set) is commonly used in various realms of software development, particularly in machine learning
For example, in feature selection for a machine learning model, it's crucial to explore different combinations of features (subsets) to see which ones contribute the most to the predictive model's accuracy
This is essentially generating the power set of features
Similarly, it is used in big data analytics, search engines, and data mining for various computation-related tasks involving sets of data

Given an array of integers nums of unique elements. Return all possible subsets (power set) of the array.

Do not include the duplicates in the answer.

Examples:

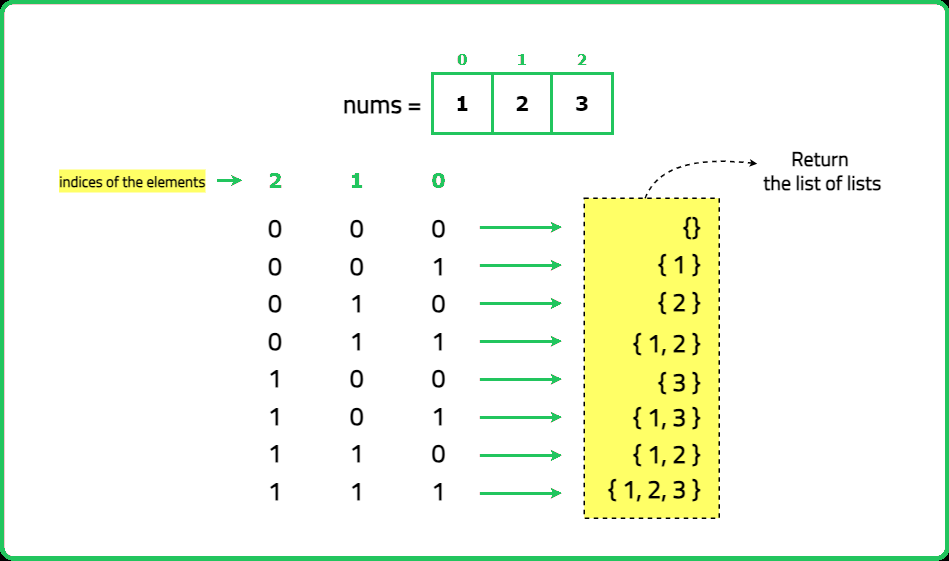
Input : nums = [1, 2, 3]

Output : [ [ ] , [1] , [2] , [1, 2] , [3] , [1, 3] , [2, 3] , [1, 2 ,3] ]

Input : nums = [1, 2]

Output : [ [ ] , [1] , [2] , [1, 2] ]

Input : nums = [0]

Constraints

1 <= nums.length <= 10
-10 <= nums[i] <= 10

Hints

"Use a recursive function that explores two choices at each step: (a) Include the current element in the subset. (b) Exclude the current element."
"Represent each subset as a bitmask of length n, where each bit indicates whether an element is included (1) or excluded (0). Iterate through all numbers from 0 to 2^n−1. For each number, use its binary representation to construct the corresponding subset."

Company Tags

Riot Games Airbnb Oracle Docker Intel Qualcomm Medtronic Instacart eBay Morgan Stanley Epic Games HashiCorp Lyft PwC NVIDIA Flipkart Rakuten Roblox Zoho Teladoc Health Dropbox Splunk Walmart Salesforce DoorDash Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition:

The power set of a given array is the set of all possible subsets of the array, including the empty set and the set itself. Each element can either be included in a subset or not, resulting in 2ⁿ (where n is the number of elements) possible subsets.

Approach:

Each subset can be represented by a binary number of length n (where n is the size of the array). If the binary number is 101, it means the subset includes the elements at positions 1 and 3 of the array.
Store the size of array, the count of subarrays in variables. Declare a list of lists to return the required answer.
Loop through all possible values from 0 to count-1. Initialize an empty list for the current subset.
For each value, use its binary representation to decide which elements are included in the current subset. Loop through each bit of the current value. If the bit is set, add the corresponding element from the array in the subset.
Add all the subsets generated to the list of list which can be returned as our answer.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function call to get the
    Power set of given array */
    vector<vector<int>> powerSet(vector<int>& nums) {
        
        // Variable to store size of array
        int n = nums.size();
        
        // To store the answer
        vector<vector<int>> ans;
        
        /* Variable to store the 
        count of total susbsets */
        int count = (1 << n);
        
        // Traverse for every value
        for(int val = 0; val < count; val++) {
            
            // To store the current subset
            vector<int> subset;
            
            // Traverse on n bits
            for(int i=0; i < n; i++) {
                if(val & (1 << i)) {
                    subset.push_back(nums[i]);
                }
            }
            
            /* Add the current subset 
            to final answer */
            ans.push_back(subset);
        }
        
        // Return stored answer
        return ans;
    }
};

int main() {
    vector<int> nums = {1, 2, 3};
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to get the
    Power set of given array */
    vector<vector<int>> ans = sol.powerSet(nums);
    
    sort(ans.begin(), ans.end());
    
    // Output
    cout << "The power set for the given array is: " << endl;
    
    for(int i=0; i < ans.size(); i++) {
        for(int j=0; j < ans[i].size(); j++) {
            cout << ans[i][j] << " ";        
        }
        cout << endl;
    }
    
    return 0;
}
import java.util.*;

class Solution {
    /* Function call to get the
    Power set of given array */
    public List<List<Integer>> powerSet(int[] nums) {
        
        // Variable to store size of array
        int n = nums.length;
        
        // To store the answer
        List<List<Integer>> ans = new ArrayList<>();
        
        /* Variable to store the 
        count of total susbsets */
        int count = (1 << n);
        
        // Traverse for every value
        for (int val = 0; val < count; val++) {
            
            // To store the current subset
            List<Integer> subset = new ArrayList<>();
            
            // Traverse on n bits
            for (int i = 0; i < n; i++) {
                if ((val & (1 << i)) != 0) {
                    subset.add(nums[i]);
                }
            }
            
            /* Add the current subset 
            to final answer */
            ans.add(subset);
        }
        
        // Return stored answer
        return ans;
    }
    
    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution(); 
        
        /* Function call to get the
        Power set of given array */
        List<List<Integer>> ans = sol.powerSet(nums);
        
        ans.sort(Comparator.comparingInt(List::size));
        
        // Output
        System.out.println("The power set for the given array is: ");
        
        for (List<Integer> subset : ans) {
            for (int num : subset) {
                System.out.print(num + " ");
            }
            System.out.println();
        }
    }
}
class Solution:
    # Function call to get the
    # Power set of given array
    def powerSet(self, nums):
        
        # Variable to store size of array
        n = len(nums)
        
        # To store the answer
        ans = []
        
        # Variable to store the 
        # count of total susbsets
        count = (1 << n)
        
        # Traverse for every value
        for val in range(count):
            
            # To store the current subset
            subset = []
            
            # Traverse on n bits
            for i in range(n):
                if val & (1 << i):
                    subset.append(nums[i])
            
            # Add the current subset 
            # to final answer 
            ans.append(subset)
        
        # Return stored answer
        return ans

# Creating an instance of Solution class
sol = Solution()

# Function call to get the Power set of given array
nums = [1, 2, 3]
ans = sol.powerSet(nums)

ans.sort(key=lambda x: len(x))

# Output
print("The power set for the given array is: ")
for subset in ans:
    print(" ".join(map(str, subset)))
class Solution {
    /* Function call to get the
    Power set of given array */
    powerSet(nums) {
        
        // Variable to store size of array
        let n = nums.length;
        
        // To store the answer
        let ans = [];
        
        /* Variable to store the 
        count of total susbsets */
        let count = (1 << n);
        
        // Traverse for every value
        for (let val = 0; val < count; val++) {
            
            // To store the current subset
            let subset = [];
            
            // Traverse on n bits
            for (let i = 0; i < n; i++) {
                if (val & (1 << i)) {
                    subset.push(nums[i]);
                }
            }
            
            /* Add the current subset 
            to final answer */
            ans.push(subset);
        }
        
        // Return stored answer
        return ans;
    }
}

// Creating an instance of Solution class
const sol = new Solution();

// Function call to get the Power set of given array
const nums = [1, 2, 3];
const ans = sol.powerSet(nums);

ans.sort((a, b) => a.length - b.length);

// Output
console.log("The power set for the given array is: ");
for (let subset of ans) {
    console.log(subset.join(" "));
}

Complexity Analysis:

Time Complexity: O(2^N*N) (where N is the size of the array) –

The outer loop runs for count numbers of times, and count is 2^N resulting in O(2^N) TC.
The inner for loop runs to check N bits, resulting in O(N) TC.

Space Complexity: O(2^N*N) – Space required to store the power set (approximately).

Code

Problem List