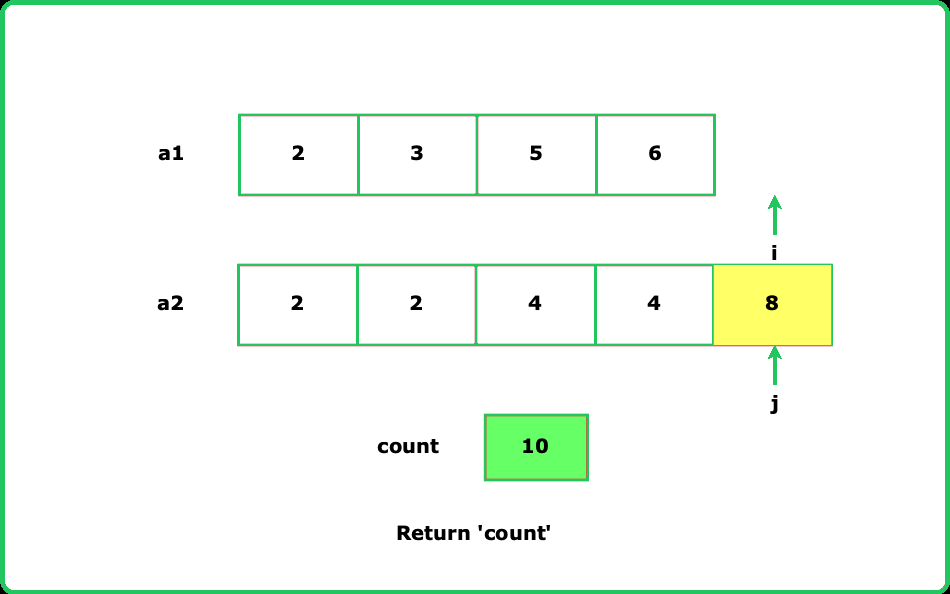
Count Inversions
Arrays
FAQs(Hard)
Hard
- Fun Fact: This problem forms the core concept behind certain algorithmic functionalities in database management systems
- When a database sorts data, it often uses similar concepts to inversion count
- For instance, it can be used in optimizing query processing
- The less the number of inversions, the more optimized the data arrangement would be
- Additionally, in search engines, the concept of inversion is used to improve search result rankings, for example in determining the best arrangement of URLs given a specific query
Given an integer array nums. Return the number of inversions in the array.
Two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j.
- It indicates how close an array is to being sorted.
- A sorted array has an inversion count of 0.
- An array sorted in descending order has maximum inversion.
Examples:
Input: nums = [2, 3, 7, 1, 3, 5]
Output: 5
Explanation: The responsible indexes are:
nums[0], nums[3], values: 2 > 1 & indexes: 0 < 3
nums[1], nums[3], values: 3 > 1 & indexes: 1 < 3
nums[2], nums[3], values: 7 > 1 & indexes: 2 < 3
nums[2], nums[4], values: 7 > 3 & indexes: 2 < 4
nums[2], nums[5], values: 7 > 5 & indexes: 2 < 5
Input: nums = [-10, -5, 6, 11, 15, 17]
Output: 0
Explanation: nums is sorted, hence no inversions present.
Input: nums = [9, 5, 4, 2]
Constraints
- 1 <= nums.length <= 105
- -104 <= nums[i] <= 104
Hints
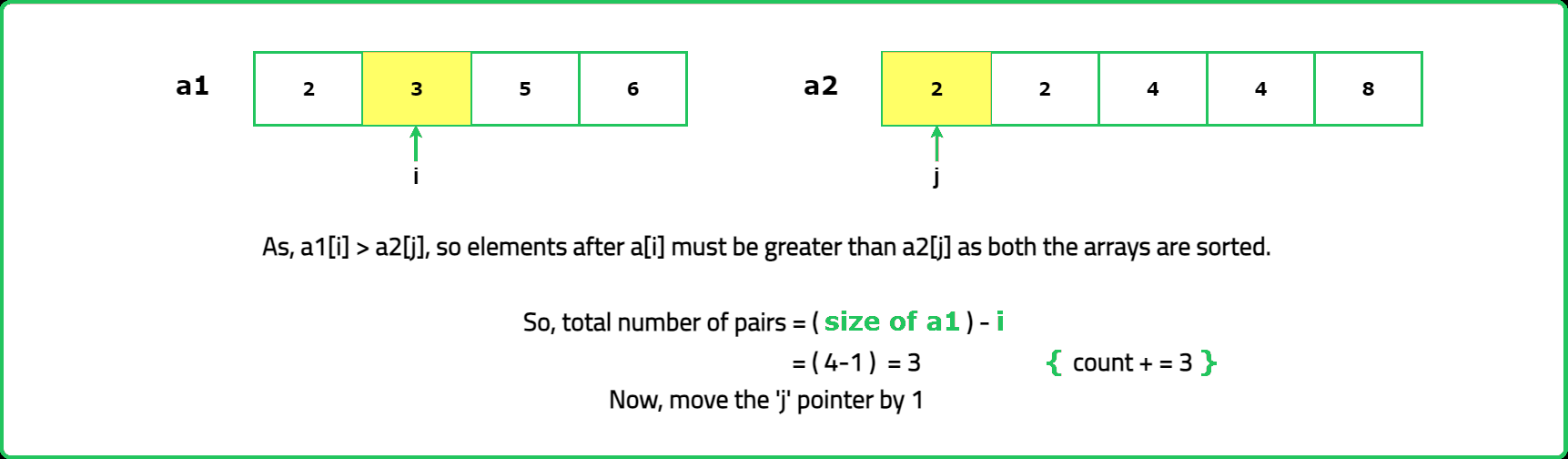
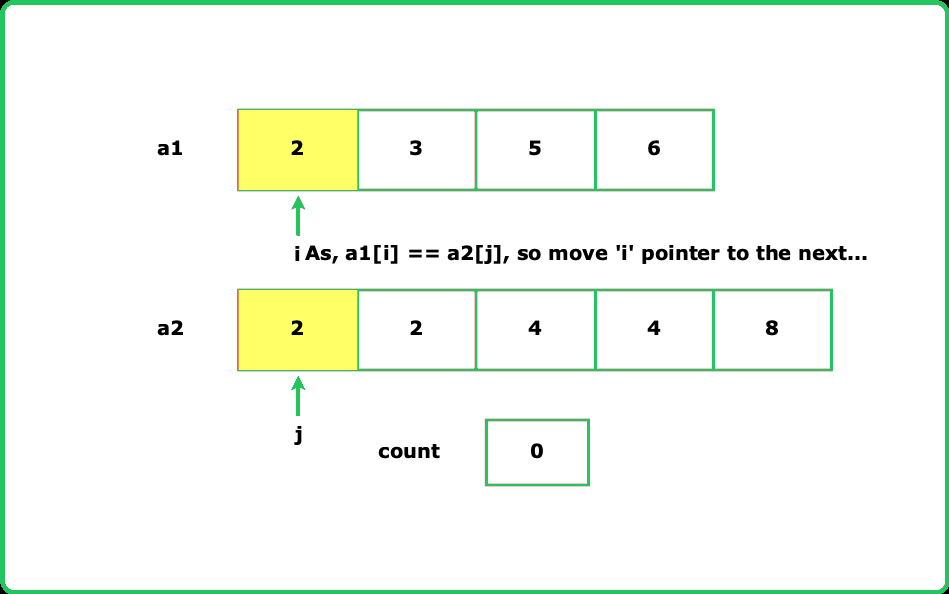
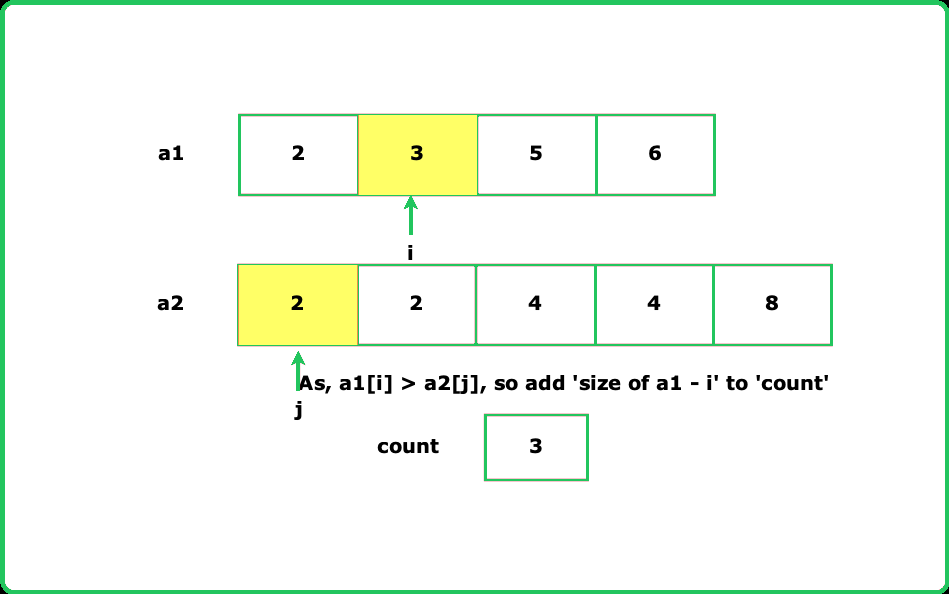
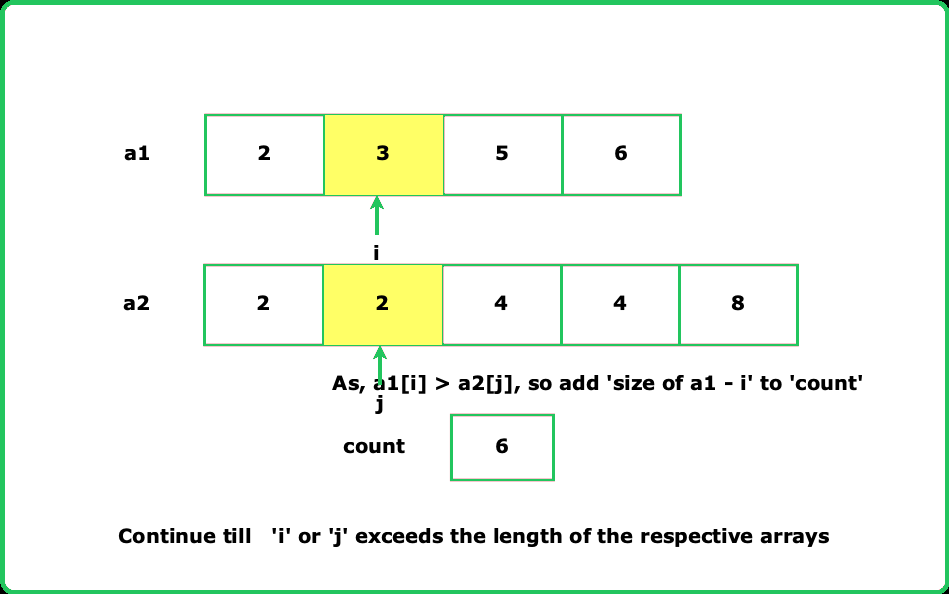
- We can use Merge Sort to count inversions efficiently in O(n log n). While merging, if nums[i] > nums[j], all elements from i onward in the left half form inversions with nums[j].
- If values in nums are bounded, a Fenwick Tree or Segment Tree can be used to count elements greater than nums[j] before index j in O(n log n).
Company Tags
Bain & Company
Mastercard
Teladoc Health
Zoho
Unity Technologies
Robinhood
NVIDIA
Salesforce
Etsy
Electronic Arts
IBM
Zomato
OYO Rooms
Docker
Bloomberg
Rockstar Games
Boston Consulting Group
Twilio
Activision Blizzard
Epic Games
Riot Games
Alibaba
MongoDB
Western Digital
Broadcom
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe