Count subsets with sum K
Dynamic Programming
DP on subsequences
Hard
- An interesting real-world application of this problem can be found in the development of algorithms for financial portfolio management systems
- These systems must often identify subsets of stocks (from a larger pool) that sum to a specific target value
- This allows fund managers to balance their portfolios for risk and return
- Counting the number of such subsets can be a part of the process to identify multiple possibilities for optimal portfolio constructions based on different risk-return preferences
Given an array arr of n integers and an integer K, count the number of subsets of the given array that have a sum equal to K. Return the result modulo 109+7.
Examples:
Input: arr = [2, 3, 5, 16, 8, 10], K = 10
Output: 3
Explanation: The subsets are [2, 8], [10], and [2, 3, 5].
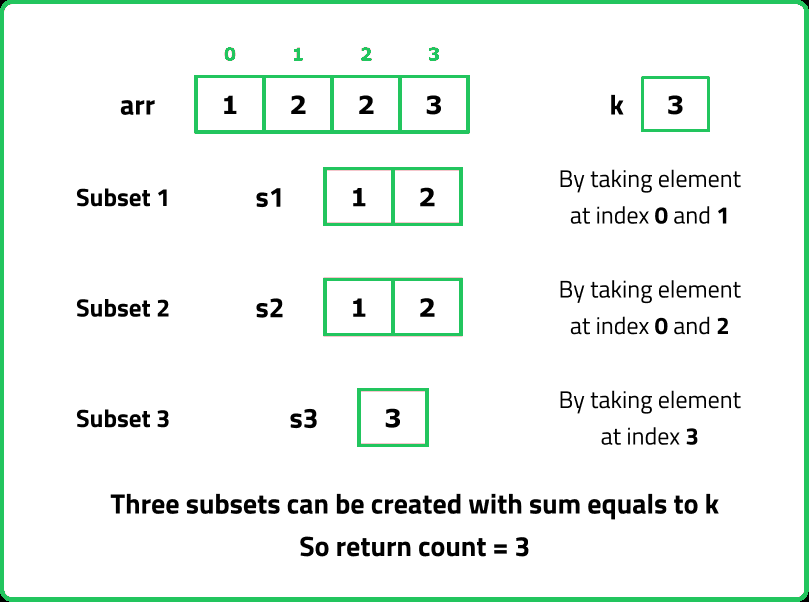
Input: arr = [1, 2, 3, 4, 5], K = 5
Output: 3
Explanation: The subsets are [5], [2, 3], and [1, 4].
Input: arr = [2, 2, 2, 2], K = 4
Constraints
- 1 <= n <= 100
- 1 <= arr[i] <= 103
- 1 <= K <= 103
Hints
- "Define dp[i][j] as the number of ways to form sum j using the first i elements of arr. If we exclude arr[i], then dp[i][j] = dp[i-1][j]. If we include arr[i], then dp[i][j] = dp[i-1][j - arr[i]] (if j ≥ arr[i])."
- "ince dp[i][j] depends only on dp[i-1][j] and dp[i-1][j - arr[i]], we can optimize to O(K) space by using a 1D DP array (dp[K]) updated from right to left: dp[j]=(dp[j]+dp[j−arr[i]])mod(10^9+7)"
Company Tags
Nutanix
Target
HashiCorp
Alibaba
Epic Games
GE Healthcare
Robinhood
Etsy
OYO Rooms
Instacart
Ernst & Young
Swiggy
Deloitte
Visa
Oracle
Byju's
Lyft
KPMG
Riot Games
Uber
Zynga
Seagate Technology
Activision Blizzard
Databricks
Chewy
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
The idea is to generate all pssible subsets and whenever a single subsets is found whose sum is equal to the given target, simply count it. As, all the subsets needs to generated, recursion can be used to solve this problem.
Steps to form the recursive solution:
- Express the problem in terms of indexes: The array will have an index but there is one more parameter “target”. So, we can say that initially, we need to find(n-1, target) which means that we are counting the number of subsets in the array from index 0 to n-1, whose sum is equal to the target.
- Try out all possible choices at a given index: As all the subsets needs to be generated, we will use the pick/non-pick technique.There will be two choices in each function call:
- Return sum of pick and not pick: As we have to return the total count of subsets with the target sum, we will return the sum of taken and notTaken from our recursive call.
- Base cases: There will be tow base cases, First, when target == 0, it means that the subset is already found from the previous steps, so simply return 1. Another, when ind==0, it means we are at the first element, so return arr[ind]==target. If the element is equal to the target it will return 1 else 0.
So, f(ind, target) will count the number of subsets that exists in the array from index 0 to 'ind', whose sum is equal to target.
Do not include the current element in the subset: First try to find a subset without considering the current index element. For this, make a recursive call to f(ind-1,target).
Include the current element in the subset: Now try to find a subset by considering the current index element as part of subset. As the current element(arr[ind]) is included, the remaining target sum will be target - arr[ind]. Therefore, make a function call of f(ind-1,target-arr[ind]).
Note: Consider the current element in the subset only when the current element is less or equal to the target.
12345678
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, target){
not pick = f(ind-1, target)
pick = 0
if(target <= arr[ind]){
pick = f(ind-1, target - arr[ind])
}
}123456789
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, target){
not pick = f(ind-1, target)
pick = 0
if(target <= arr[ind]){
pick = f(ind-1, target - arr[ind])
}
return pick + not pick
}1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
#include <bits/stdc++.h>
using namespace std;
class Solution{
int modulo = 1e9+7;
private:
/*Function to count the number of
subsets with sum k using recursion*/
int findWaysUtil(int ind, int target, vector<int>& arr) {
/* Base case: If the target sum
is 0, we found a valid subset*/
if (target == 0)
return 1;
/* Base case: If we have considered all elements
and the target is still not 0, return 0*/
if (ind == 0)
return (arr[0] == target) ? 1 : 0;
// Exclude the current element
int notTaken = findWaysUtil(ind - 1, target, arr);
/* Include the current element if
it doesn't exceed the target*/
int taken = 0;
if (arr[ind] <= target)
taken = findWaysUtil(ind - 1, target - arr[ind], arr);
/* Return the result. Also, take
modulo for the code to be accepted*/
return (notTaken + taken)%modulo;
}
public:
//Function to find out number of subsets with sum k
int perfectSum(vector<int>&arr, int K){
int n = arr.size();
//Return the result
return findWaysUtil(n - 1, K, arr);
}
};
int main() {
vector<int> arr = {1, 2, 2, 3};
int k = 3;
//Create an instance of Solution class
Solution sol;
//Print the result
cout << "The number of subsets found are " << sol.perfectSum(arr, k);
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
import java.util.Arrays;
class Solution {
private static final int MODULO = 1000000007;
/* Function to count the number of
subsets with sum k using recursion */
private int findWaysUtil(int ind, int target, int[] arr) {
/* Base case: If the target sum
is 0, we found a valid subset */
if (target == 0)
return 1;
/* Base case: If we have considered all elements
and the target is still not 0, return 0 */
if (ind == 0)
return (arr[0] == target) ? 1 : 0;
// Exclude the current element
int notTaken = findWaysUtil(ind - 1, target, arr);
/* Include the current element if
it doesn't exceed the target */
int taken = 0;
if (arr[ind] <= target)
taken = findWaysUtil(ind - 1, target - arr[ind], arr);
/* Return the result. Also, take
modulo for the code to be accepted*/
return (notTaken + taken) % MODULO;
}
// Function to find out number of subsets with sum k
public int perfectSum(int[] arr, int K) {
int n = arr.length;
// Return the result
return findWaysUtil(n - 1, K, arr);
}
public static void main(String[] args) {
int[] arr = {1, 2, 2, 3};
int k = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("The number of subsets found are " + sol.perfectSum(arr, k));
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
MODULO = 10**9 + 7
class Solution:
""" Function to count the number of
subsets with sum k using recursion """
def findWaysUtil(self, ind, target, arr):
""" Base case: If the target sum
is 0, we found a valid subset """
if target == 0:
return 1
""" Base case: If we have considered all elements
and the target is still not 0, return 0 """
if ind == 0:
return 1 if arr[0] == target else 0
# Exclude the current element
notTaken = self.findWaysUtil(ind - 1, target, arr)
""" Include the current element if
it doesn't exceed the target"""
taken = 0
if arr[ind] <= target:
taken = self.findWaysUtil(ind - 1, target - arr[ind], arr)
""" Return the result. Also, take
modulo for the code to be accepted"""
return (notTaken + taken) % MODULO
# Function to find out number of subsets with sum k
def perfectSum(self, arr, K):
n = len(arr)
# Return the result
return self.findWaysUtil(n - 1, K, arr)
if __name__ == "__main__":
arr = [1, 2, 2, 3]
k = 3
#Create an instance of Solution class
sol = Solution()
#Print the result
print(f"The number of subsets found are {sol.perfectSum(arr, k)}")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
const MODULO = 1e9 + 7;
class Solution {
/* Function to count the number of
subsets with sum k using recursion */
findWaysUtil(ind, target, arr) {
/* Base case: If the target sum
is 0, we found a valid subset */
if (target === 0)
return 1;
/* Base case: If we have considered all elements
and the target is still not 0, return 0 */
if (ind === 0)
return arr[0] === target ? 1 : 0;
// Exclude the current element
const notTaken = this.findWaysUtil(ind - 1, target, arr);
/* Include the current element if
it doesn't exceed the target */
let taken = 0;
if (arr[ind] <= target)
taken = this.findWaysUtil(ind - 1, target - arr[ind], arr);
/* Return the result. Also, take
modulo for the code to be accepted*/
return (notTaken + taken) % MODULO;
}
// Function to find out number of subsets with sum k
perfectSum(arr, K) {
const n = arr.length;
// Return the result
return this.findWaysUtil(n - 1, K, arr);
}
}
const arr = [1, 2, 2, 3];
const k = 3;
//Create an instance of Solution class
const sol = new Solution();
//Print the result
console.log(`The number of subsets found are ${sol.perfectSum(arr, k)}`);
Complexity Analysis:
Time Complexity: O(2(N)), where N is the length of the array. As, for each index, ther are two possible options.Space Complexity:O(N), at maximum the depth of the recursive stack can go upto N.
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
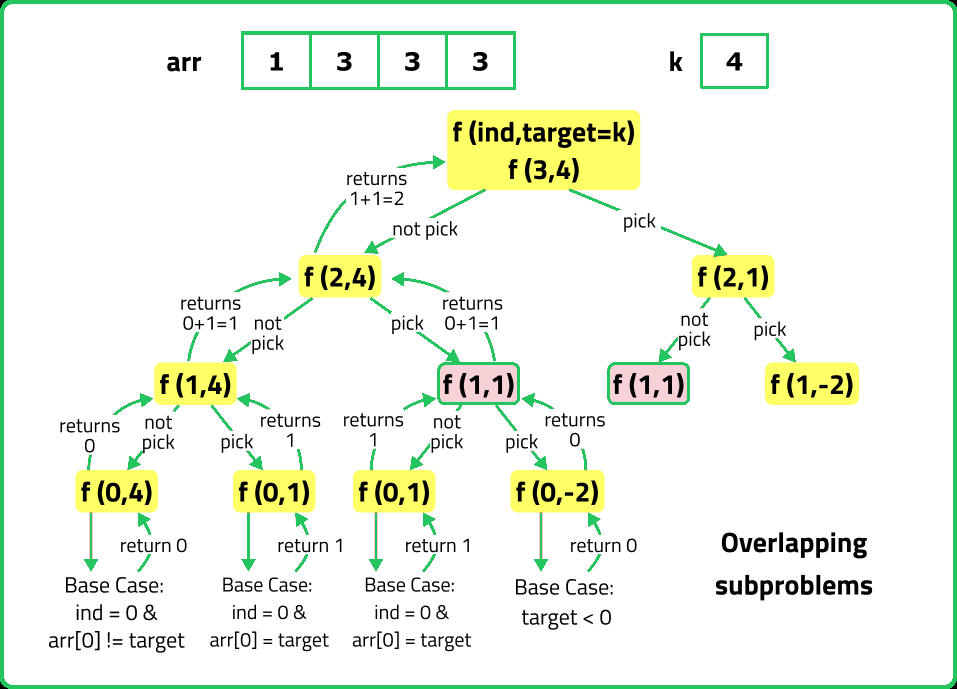
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'target' only values between 0 to target. Therefore, we need 2D dp array.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263
#include <bits/stdc++.h>
using namespace std;
class Solution{
int modulo = 1e9+7;
private:
/*Function to count the number of
subsets with sum k using memoization*/
int findWaysUtil(int ind, int target, vector<int>& arr, vector<vector<int>>& dp) {
/* Base case: If the target sum
is 0, we found a valid subset*/
if (target == 0)
return 1;
/* Base case: If we have considered all elements
and the target is still not 0, return 0*/
if (ind == 0)
return (arr[0] == target) ? 1 : 0;
/* If the result for this state
is already calculated, return it*/
if (dp[ind][target] != -1)
return dp[ind][target];
// Exclude the current element
int notTaken = findWaysUtil(ind - 1, target, arr, dp);
/* Include the current element if
it doesn't exceed the target*/
int taken = 0;
if (arr[ind] <= target)
taken = findWaysUtil(ind - 1, target - arr[ind], arr, dp);
/* Store the result in DP table and return
Also, take modulo for the code to be accepted*/
return dp[ind][target] = (notTaken + taken)%modulo;
}
public:
//Function to find out number of subsets with sum k
int perfectSum(vector<int>&arr, int K){
int n = arr.size();
//DP array to store the subproblems
vector<vector<int>> dp(n, vector<int>(K + 1, -1));
//Return the result
return findWaysUtil(n - 1, K, arr, dp);
}
};
int main() {
vector<int> arr = {1, 2, 2, 3};
int k = 3;
//Create an instance of Solution class
Solution sol;
//Print the result
cout << "The number of subsets found are " << sol.perfectSum(arr, k);
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162
import java.util.Arrays;
class Solution {
private static final int MODULO = 1000000007;
/* Function to count the number of
subsets with sum k using memoization */
private int findWaysUtil(int ind, int target, int[] arr, int[][] dp) {
/* Base case: If the target sum
is 0, we found a valid subset */
if (target == 0)
return 1;
/* Base case: If we have considered all elements
and the target is still not 0, return 0 */
if (ind == 0)
return (arr[0] == target) ? 1 : 0;
/* If the result for this state
is already calculated, return it */
if (dp[ind][target] != -1)
return dp[ind][target];
// Exclude the current element
int notTaken = findWaysUtil(ind - 1, target, arr, dp);
/* Include the current element if
it doesn't exceed the target */
int taken = 0;
if (arr[ind] <= target)
taken = findWaysUtil(ind - 1, target - arr[ind], arr, dp);
/* Store the result in DP table and return
Also, take modulo for the code to be accepted*/
return dp[ind][target] = (notTaken + taken) % MODULO;
}
// Function to find out number of subsets with sum k
public int perfectSum(int[] arr, int K) {
int n = arr.length;
// DP array to store the subproblems
int[][] dp = new int[n][K + 1];
for (int[] row : dp) {
Arrays.fill(row, -1);
}
// Return the result
return findWaysUtil(n - 1, K, arr, dp);
}
public static void main(String[] args) {
int[] arr = {1, 2, 2, 3};
int k = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("The number of subsets found are " + sol.perfectSum(arr, k));
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354
MODULO = 10**9 + 7
class Solution:
""" Function to count the number of
subsets with sum k using memoization """
def findWaysUtil(self, ind, target, arr, dp):
""" Base case: If the target sum
is 0, we found a valid subset """
if target == 0:
return 1
""" Base case: If we have considered all elements
and the target is still not 0, return 0 """
if ind == 0:
return 1 if arr[0] == target else 0
""" If the result for this state
is already calculated, return it """
if dp[ind][target] != -1:
return dp[ind][target]
# Exclude the current element
notTaken = self.findWaysUtil(ind - 1, target, arr, dp)
""" Include the current element if
it doesn't exceed the target"""
taken = 0
if arr[ind] <= target:
taken = self.findWaysUtil(ind - 1, target - arr[ind], arr, dp)
"""Store the result in DP table and return
Also, take modulo for the code to be accepted"""
dp[ind][target] = (notTaken + taken) % MODULO
return dp[ind][target]
# Function to find out number of subsets with sum k
def perfectSum(self, arr, K):
n = len(arr)
# DP array to store the subproblems
dp = [[-1] * (K + 1) for _ in range(n)]
# Return the result
return self.findWaysUtil(n - 1, K, arr, dp)
if __name__ == "__main__":
arr = [1, 2, 2, 3]
k = 3
#Create an instance of Solution class
sol = Solution()
#Print the result
print(f"The number of subsets found are {sol.perfectSum(arr, k)}")
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
const MODULO = 1e9 + 7;
class Solution {
/* Function to count the number of
subsets with sum k using memoization */
findWaysUtil(ind, target, arr, dp) {
/* Base case: If the target sum
is 0, we found a valid subset */
if (target === 0)
return 1;
/* Base case: If we have considered all elements
and the target is still not 0, return 0 */
if (ind === 0)
return arr[0] === target ? 1 : 0;
/* If the result for this state
is already calculated, return it */
if (dp[ind][target] !== -1)
return dp[ind][target];
// Exclude the current element
const notTaken = this.findWaysUtil(ind - 1, target, arr, dp);
/* Include the current element if
it doesn't exceed the target */
let taken = 0;
if (arr[ind] <= target)
taken = this.findWaysUtil(ind - 1, target - arr[ind], arr, dp);
/* Store the result in DP table and return
Also, take modulo for the code to be accepted*/
dp[ind][target] = (notTaken + taken) % MODULO;
return dp[ind][target];
}
// Function to find out number of subsets with sum k
perfectSum(arr, K) {
const n = arr.length;
// DP array to store the subproblems
const dp = Array.from({ length: n }, () => Array(K + 1).fill(-1));
// Return the result
return this.findWaysUtil(n - 1, K, arr, dp);
}
}
const arr = [1, 2, 2, 3];
const k = 3;
//Create an instance of Solution class
const sol = new Solution();
//Print the result
console.log(`The number of subsets found are ${sol.perfectSum(arr, k)}`);
Complexity Analysis:
Time Complexity: O(N*target), There are 'N*target' states therefore at max ‘N*target’ new problems will be solved.Space Complexity:O(N*target) + O(N), As we are using a recursion stack space(O(N)) and a 2D array ( O(N*target)).
To convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n) and including 0 its n, where n is the size of array, for 'target' can have any values between 0 to 'target'. So we need a 2D dp array. Set its type as int and initialize it as 0.
- Setting Base Cases in the Array: In the recursive code, our base condition was when target == 0, it means the required subset is found and we were returning 1. So, set '1' in the dp array for every index where target = 0.
- Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.
- Returning the answer: At last dp[n-1][target] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.
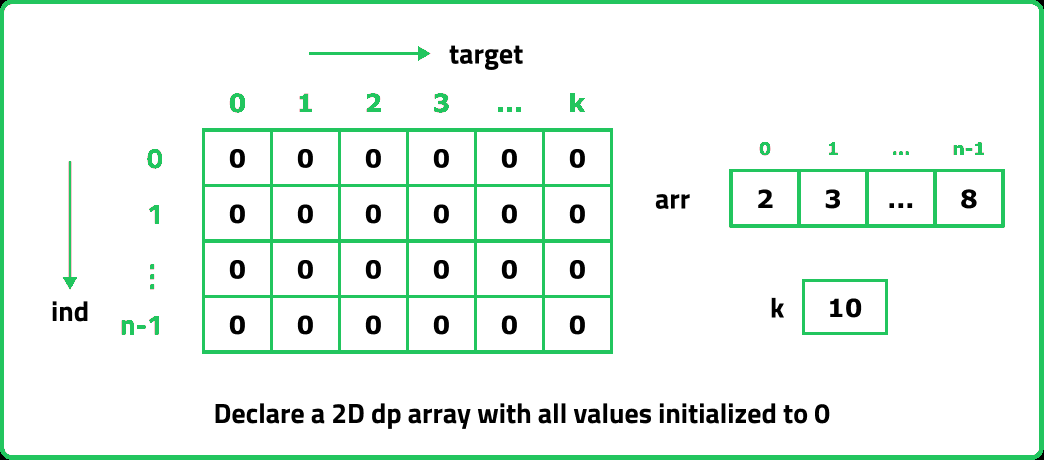
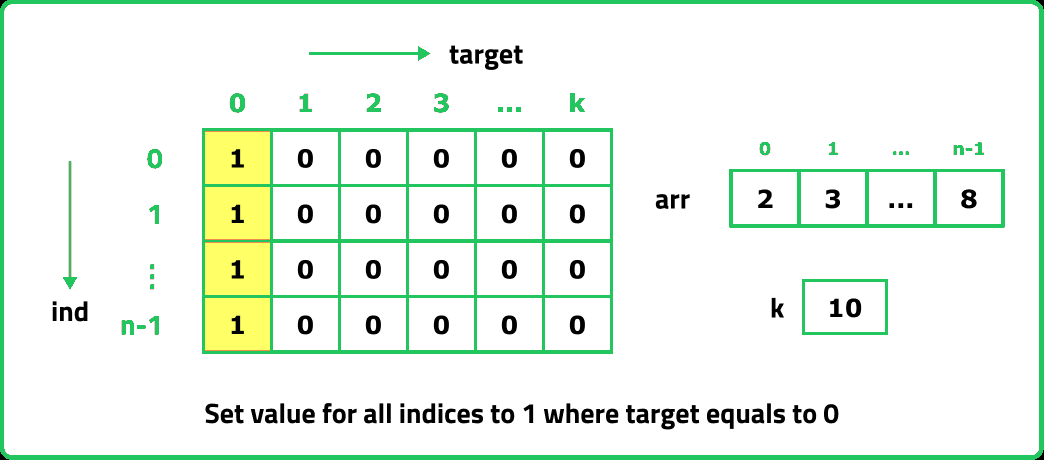
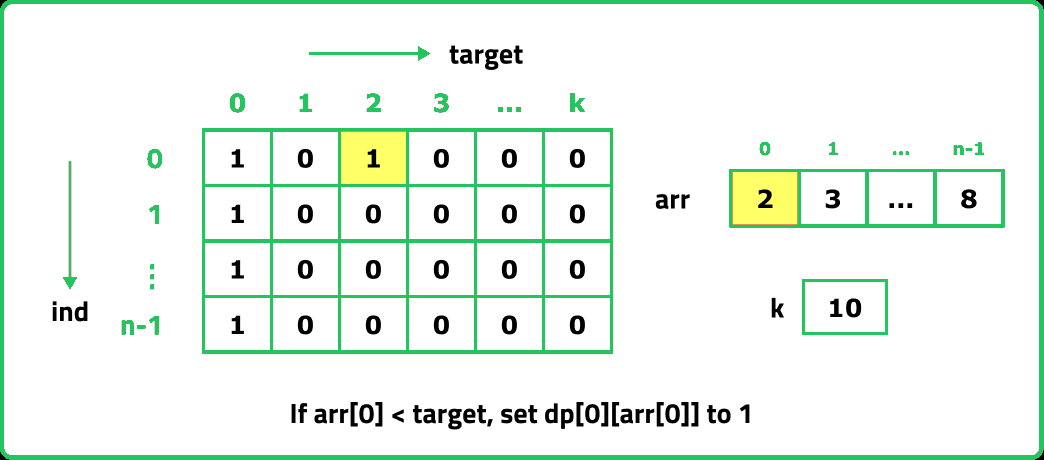
The first row dp[0][] indicates that only the first element of the array is considered, therefore for the target value equal to arr[0], only cell with that target will be true, so explicitly set dp[0][arr[0]] =1, (dp[0][arr[0]] means that we are considering the first element of the array with the target equal to the first element itself). Please note that it can happen that arr[0]>target, so we first check it: if(arr[0]<=target) then set dp[0][arr[0]] = 1
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
#include <bits/stdc++.h>
using namespace std;
class Solution{
int modulo = 1e9+7;
public:
//Function to find out number of subsets with sum k
int perfectSum(vector<int>&arr, int K){
int n = arr.size();
/* Create a 2D DP table with dimensions
n x k+1, initialized with zeros*/
vector<vector<int>> dp(n, vector<int>(K + 1, 0));
/* Base case: If the target sum is 0, there
is one valid subset (the empty subset)*/
for (int i = 0; i < n; i++) {
dp[i][0] = 1;
}
/* Initialize the first row based
on the first element of the array*/
if (arr[0] <= K) {
dp[0][arr[0]] = 1;
}
// Fill in the DP table using a bottom-up approach
for (int ind = 1; ind < n; ind++) {
for (int target = 1; target <= K; target++) {
// Exclude the current element
int notTaken = dp[ind - 1][target];
/* Include the current element
if it doesn't exceed the target*/
int taken = 0;
if (arr[ind] <= target) {
taken = (dp[ind - 1][target - arr[ind]]) % modulo;
}
/* Update the DP table and take
modulo for the code to be accepted*/
dp[ind][target] = (notTaken + taken)%modulo;
}
}
// The final result is in the last cell of table
return dp[n - 1][K];
}
};
int main() {
vector<int> arr = {1, 2, 2, 3};
int k = 3;
//Create an instance of Solution class
Solution sol;
//Print the result
cout << "The number of subsets found are " << sol.perfectSum(arr, k);
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960
import java.util.*;
class Solution {
private static final int MODULO = 1000000007;
// Function to find out number of subsets with sum k
public int perfectSum(int[] arr, int K) {
int n = arr.length;
/* Create a 2D DP table with dimensions
n x k+1, initialized with zeros */
int[][] dp = new int[n][K + 1];
/* Base case: If the target sum is 0, there
is one valid subset (the empty subset) */
for (int i = 0; i < n; i++) {
dp[i][0] = 1;
}
/* Initialize the first row based
on the first element of the array */
if (arr[0] <= K) {
dp[0][arr[0]] = 1;
}
// Fill in the DP table using a bottom-up approach
for (int ind = 1; ind < n; ind++) {
for (int target = 1; target <= K; target++) {
// Exclude the current element
int notTaken = dp[ind - 1][target];
/* Include the current element
if it doesn't exceed the target */
int taken = 0;
if (arr[ind] <= target) {
taken = dp[ind - 1][target - arr[ind]] % MODULO;
}
/* Update the DP table and take
modulo for the code to be accepted */
dp[ind][target] = (notTaken + taken) % MODULO;
}
}
// The final result is in the last cell of table
return dp[n - 1][K];
}
public static void main(String[] args) {
int[] arr = {1, 2, 2, 3};
int k = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("The number of subsets found are " + sol.perfectSum(arr, k));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
MODULO = 10**9 + 7
class Solution:
# Function to find out number of subsets with sum k
def perfectSum(self, arr, K):
n = len(arr)
""" Create a 2D DP table with dimensions
n x k+1, initialized with zeros"""
dp = [[0] * (K + 1) for _ in range(n)]
""" Base case: If the target sum is 0, there
is one valid subset (the empty subset)"""
for i in range(n):
dp[i][0] = 1
""" Initialize the first row based
on the first element of the array"""
if arr[0] <= K:
dp[0][arr[0]] = 1
# Fill in the DP table using a bottom-up approach
for ind in range(1, n):
for target in range(1, K + 1):
# Exclude the current element
notTaken = dp[ind - 1][target]
""" Include the current element if
it doesn't exceed the target"""
taken = 0
if arr[ind] <= target:
taken = dp[ind - 1][target - arr[ind]] % MODULO
""" Update the DP table and take
modulo for the code to be accepted"""
dp[ind][target] = (notTaken + taken) % MODULO
# The final result is in the last cell of table
return dp[n - 1][K]
if __name__ == "__main__":
arr = [1, 2, 2, 3]
k = 3
#Create an instance of Solution class
sol = Solution()
#Print the answer
print(f"The number of subsets found are {sol.perfectSum(arr, k)}")
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
const MODULO = 1e9 + 7;
class Solution {
// Function to find out number of subsets with sum k
perfectSum(arr, K) {
const n = arr.length;
/* Create a 2D DP table with dimensions
n x k+1, initialized with zeros*/
const dp = Array.from({ length: n }, () => Array(K + 1).fill(0));
/* Base case: If the target sum is 0,
there is one valid subset (the empty subset)*/
for (let i = 0; i < n; i++) {
dp[i][0] = 1;
}
/* Initialize the first row based
on the first element of the array*/
if (arr[0] <= K) {
dp[0][arr[0]] = 1;
}
// Fill in the DP table using a bottom-up approach
for (let ind = 1; ind < n; ind++) {
for (let target = 1; target <= K; target++) {
// Exclude the current element
const notTaken = dp[ind - 1][target];
/* Include the current element
if it doesn't exceed the target*/
let taken = 0;
if (arr[ind] <= target) {
taken = dp[ind - 1][target - arr[ind]] % MODULO;
}
/* Update the DP table and take
modulo for the code to be accepted*/
dp[ind][target] = (notTaken + taken) % MODULO;
}
}
// The final result is in the last cell of table
return dp[n - 1][K];
}
}
const arr = [1, 2, 2, 3];
const k = 3;
//Create an instance of Solution class
const sol = new Solution();
//Print the result
console.log(`The number of subsets found are ${sol.perfectSum(arr, k)}`);
Complexity Analysis:
Time Complexity: O(N*target), As, here are three nested loops that account for O(N*target) complexity.Space Complexity:O(N*target), As a 2D array of size N*target is used.
If we observe the relation, dp[ind][target] = dp[ind-1][target] + dp[ind-1][target-arr[ind]]. We find that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it.
Steps to space optimize the tabulation approach:
- Decalre an array of size target to store the previous row of the DP table. Initialize the first row and first column of the DP table based on the base conditions discussed in tabulation.
- Now, initiate two nested loops in bottom-up approach. The first loop will run for 'ind' and the second loop will run for the 'target' variable.
- In order to store the current row of the DP table, initialize a new array 'cur' and fill the first cell to 1 for base condition.
- Do the calculations for 'cur' row by performing the pick/non-pick technique used in previous approaches.
- Now, update the previous row with the current row for the next iteration and at last return the final result stored in the last cell of the previous row(prev[k]).
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
#include <bits/stdc++.h>
using namespace std;
class Solution{
int modulo = 1e9+7;
public:
//Function to find out number of subsets with sum k
int perfectSum(vector<int>&arr, int K){
int n = arr.size();
/* Initialize a vector 'prev' to represent
the previous row of the DP table*/
vector<int> prev(K + 1, 0);
/* Base case: If the target sum is 0,
there is one valid subset (the empty subset)*/
prev[0] = 1;
/* Initialize the first row based
on the first element of the array*/
if (arr[0] <= K) {
prev[arr[0]] = 1;
}
/* Fill in the DP table
using a bottom-up approach*/
for (int ind = 1; ind < n; ind++) {
/* Create a vector 'cur' to represent
the current row of the DP table*/
vector<int> cur(K + 1, 0);
cur[0] = 1;
for (int target = 1; target <= K; target++) {
// Exclude the current element
int notTaken = prev[target];
/* Include the current element
if it doesn't exceed the target*/
int taken = 0;
if (arr[ind] <= target) {
taken = prev[target - arr[ind]];
}
// Update the current row of the DP table
cur[target] = (notTaken + taken)%modulo;
}
// Set 'cur' as 'prev' for the next iteration
prev = cur;
}
/* The final result is in the
last cell of the 'prev' vector*/
return prev[K];
}
};
int main() {
vector<int> arr = {1, 2, 2, 3};
int k = 3;
//Create an instance of Solution class
Solution sol;
//Print the result
cout << "The number of subsets found are " << sol.perfectSum(arr, k);
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
import java.util.*;
class Solution {
private static final int MODULO = 1000000007;
// Function to find out number of subsets with sum k
public int perfectSum(int[] arr, int K) {
int n = arr.length;
/* Initialize a vector 'prev' to represent
the previous row of the DP table */
int[] prev = new int[K + 1];
Arrays.fill(prev, 0);
/* Base case: If the target sum is 0,
there is one valid subset (the empty subset) */
prev[0] = 1;
/* Initialize the first row based
on the first element of the array */
if (arr[0] <= K) {
prev[arr[0]] = 1;
}
/* Fill in the DP table
using a bottom-up approach */
for (int ind = 1; ind < n; ind++) {
/* Create a vector 'cur' to represent
the current row of the DP table */
int[] cur = new int[K + 1];
Arrays.fill(cur, 0);
cur[0] = 1;
for (int target = 1; target <= K; target++) {
// Exclude the current element
int notTaken = prev[target];
/* Include the current element
if it doesn't exceed the target */
int taken = 0;
if (arr[ind] <= target) {
taken = prev[target - arr[ind]];
}
// Update the current row of the DP table
cur[target] = (notTaken + taken) % MODULO;
}
// Set 'cur' as 'prev' for the next iteration
prev = cur;
}
/* The final result is in the
last cell of the 'prev' vector */
return prev[K];
}
public static void main(String[] args) {
int[] arr = {1, 2, 2, 3};
int k = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("The number of subsets found are " + sol.perfectSum(arr, k));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859
MODULO = 10**9 + 7
class Solution:
# Function to find out number of subsets with sum k
def perfectSum(self, arr, K):
n = len(arr)
""" Initialize a vector 'prev' to represent
the previous row of the DP table"""
prev = [0] * (K + 1)
""" Base case: If the target sum is 0,
there is one valid subset (the empty subset)"""
prev[0] = 1
""" Initialize the first row based
on the first element of the array"""
if arr[0] <= K:
prev[arr[0]] = 1
""" Fill in the DP table
using a bottom-up approach"""
for ind in range(1, n):
""" Create a vector 'cur' to represent
the current row of the DP table"""
cur = [0] * (K + 1)
cur[0] = 1
for target in range(1, K + 1):
# Exclude the current element
notTaken = prev[target]
""" Include the current element
if it doesn't exceed the target"""
taken = 0
if arr[ind] <= target:
taken = prev[target - arr[ind]]
# Update the current row of the DP table
cur[target] = (notTaken + taken) % MODULO
# Set 'cur' as 'prev' for the next iteration
prev = cur
""" The final result is in the
last cell of the 'prev' vector"""
return prev[K]
if __name__ == "__main__":
arr = [1, 2, 2, 3]
k = 3
#Create an instance of Solution class
sol = Solution()
#Print the result
print(f"The number of subsets found are {sol.perfectSum(arr, k)}")
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
const MODULO = 1e9 + 7;
class Solution {
// Function to find out number of subsets with sum k
perfectSum(arr, K) {
const n = arr.length;
/* Initialize a vector 'prev' to represent
the previous row of the DP table*/
let prev = new Array(K + 1).fill(0);
/* Base case: If the target sum is 0,
there is one valid subset (the empty subset)*/
prev[0] = 1;
/* Initialize the first row based
on the first element of the array*/
if (arr[0] <= K) {
prev[arr[0]] = 1;
}
/* Fill in the DP table
using a bottom-up approach*/
for (let ind = 1; ind < n; ind++) {
/* Create a vector 'cur' to represent
the current row of the DP table*/
let cur = new Array(K + 1).fill(0);
cur[0] = 1;
for (let target = 1; target <= K; target++) {
// Exclude the current element
let notTaken = prev[target];
/* Include the current element
if it doesn't exceed the target*/
let taken = 0;
if (arr[ind] <= target) {
taken = prev[target - arr[ind]];
}
// Update the current row of the DP table
cur[target] = (notTaken + taken) % MODULO;
}
// Set 'cur' as 'prev' for the next iteration
prev = cur;
}
/* The final result is in the
last cell of the 'prev' vector*/
return prev[K];
}
}
const arr = [1, 2, 2, 3];
const k = 3;
//Create an instance of Solution class
const sol = new Solution();
//Print the result
console.log(`The number of subsets found are ${sol.perfectSum(arr, k)}`);
Complexity Analysis:
Time Complexity: O(N*target), As, here are three nested loops that account for O(N*target) complexity.Space Complexity:O(target), As we are using an external array of size ‘K+1’ to store only one row.
Frequently Occurring Doubts
Q: Can a greedy approach work instead of DP?
A: No, because a greedy approach fails when elements must be selected in a specific order.
Interview Followup Questions
Q: How would you modify this problem to return the actual subsets instead of just counting them?
A: Maintain a backtracking path (dp[i][j] storing contributing elements) to reconstruct subsets.
Q: How does this problem relate to subset sum with multiplicity?
A: If elements can be used multiple times, modify DP as: dp[j]=dp[j]+dp[j−arr[i]]
Notes
Code
✅ Testcase
Input: {'K': '10', 'arr': '[2, 3, 5, 16, 8, 10]'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting
Input: {'K': '5', 'arr': '[1, 2, 3, 4, 5]'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting
Input: {'K': '4', 'arr': '[2, 2, 2, 2]'}
Expected:
6
6
Actual: -
Time: -
sec
Status: Waiting