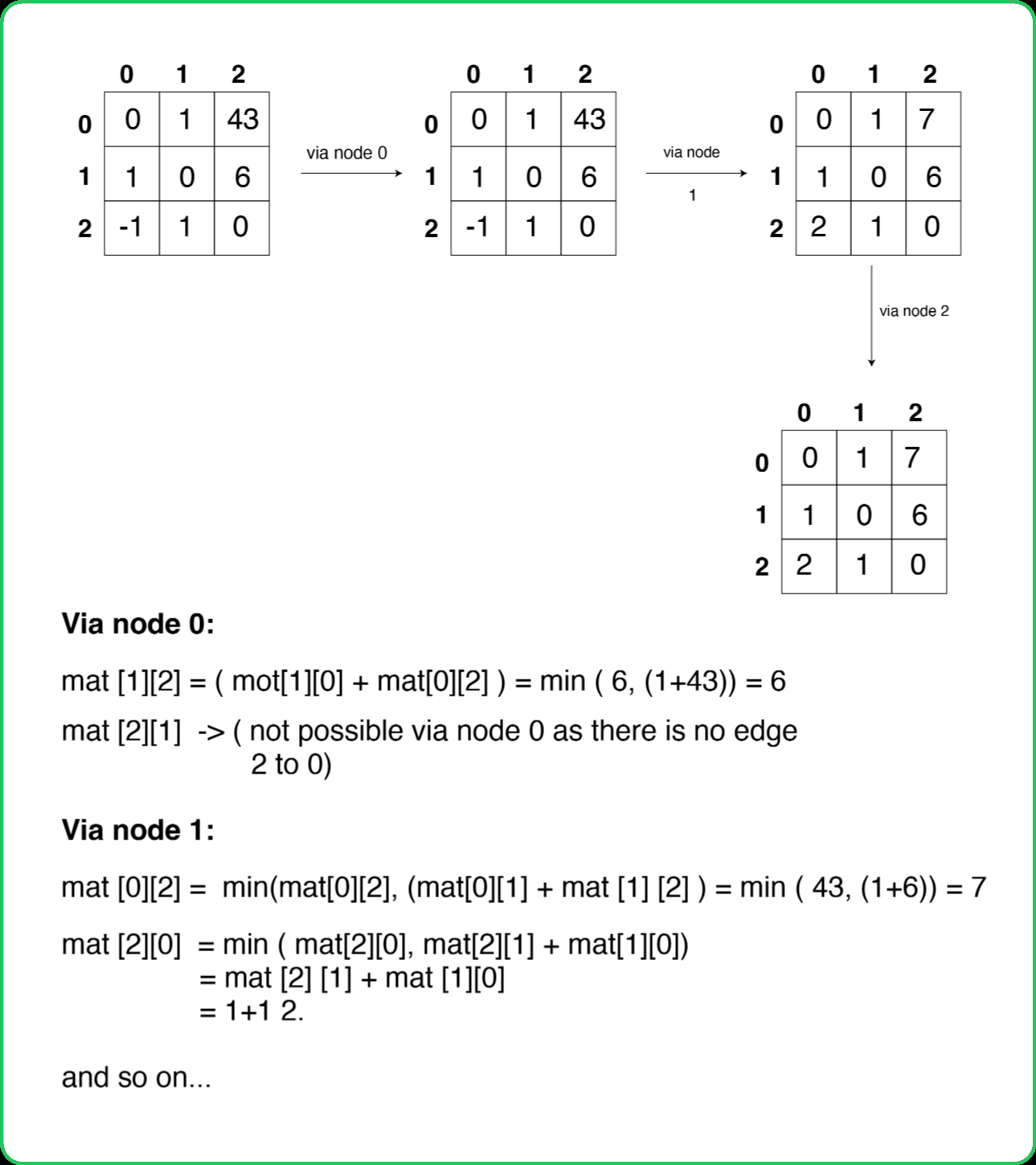
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the shortest distance
between every pair of vertices. */
void shortest_distance(vector<vector<int>> &matrix){
// Getting the number of nodes
int n = matrix.size();
// For each intermediate node k
for(int k=0; k<n; k++) {
// Check for every (i, j) pair of nodes
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
/* If k is not an intermediate
node, skip the iteration */
if(matrix[i][k] == -1 ||
matrix[k][j] == -1)
continue;
/* If no direct edge from
i to v is present */
if(matrix[i][j] == -1) {
// Update the distance
matrix[i][j] =
matrix[i][k] + matrix[k][j];
}
/* Else update the distance to
minimum of both paths */
else {
matrix[i][j] =
min(matrix[i][j] ,
matrix[i][k] + matrix[k][j]
);
}
}
}
}
}
};
int main() {
vector<vector<int>> matrix ={
{0, 2, -1, -1},
{1, 0, 3, -1},
{-1, -1, 0, -1},
{3, 5, 4, 0}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function to find the shortest distance
between every pair of vertices. */
sol.shortest_distance(matrix);
// Output
int n = matrix.size();
cout << "The shortest distance matrix is:\n";
for(int i=0; i < n; i++) {
for(int j=0; j < n; j++) {
cout << matrix[i][j] << " ";
}
cout << endl;
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869
import java.util.Arrays;
class Solution {
/* Function to find the shortest distance
between every pair of vertices. */
public void shortest_distance(int[][] matrix) {
// Getting the number of nodes
int n = matrix.length;
// For each intermediate node k
for (int k = 0; k < n; k++) {
// Check for every (i, j) pair of nodes
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
/* If k is not an intermediate
node, skip the iteration */
if (matrix[i][k] == -1 || matrix[k][j] == -1)
continue;
/* If no direct edge from
i to v is present */
if (matrix[i][j] == -1) {
// Update the distance
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
/* Else update the distance to
minimum of both paths */
else {
matrix[i][j] = Math.min(matrix[i][j], matrix[i][k] + matrix[k][j]);
}
}
}
}
}
public static void main(String[] args) {
int[][] matrix = {
{0, 2, -1, -1},
{1, 0, 3, -1},
{-1, -1, 0, -1},
{3, 5, 4, 0}
};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function to find the shortest distance
between every pair of vertices. */
sol.shortest_distance(matrix);
// Output
int n = matrix.length;
System.out.println("The shortest distance matrix is:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253
class Solution:
# Function to find the shortest distance
# between every pair of vertices.
def shortest_distance(self, matrix):
# Getting the number of nodes
n = len(matrix)
# For each intermediate node k
for k in range(n):
# Check for every (i, j) pair of nodes
for i in range(n):
for j in range(n):
# If k is not an intermediate
# node, skip the iteration
if matrix[i][k] == -1 or matrix[k][j] == -1:
continue
# If no direct edge from
# i to v is present
if matrix[i][j] == -1:
# Update the distance
matrix[i][j] = matrix[i][k] + matrix[k][j]
# Else update the distance to
# minimum of both paths
else:
matrix[i][j] = min(matrix[i][j], matrix[i][k] + matrix[k][j])
# Example usage
matrix = [
[0, 2, -1, -1],
[1, 0, 3, -1],
[-1, -1, 0, -1],
[3, 5, 4, 0]
]
# Creating an instance of
# Solution class
sol = Solution()
# Function to find the shortest distance
# between every pair of vertices.
sol.shortest_distance(matrix)
# Output
print("The shortest distance matrix is:")
for row in matrix:
print(" ".join(map(str, row)))
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960
class Solution {
/* Function to find the shortest distance
between every pair of vertices. */
shortest_distance(matrix) {
// Getting the number of nodes
let n = matrix.length;
// For each intermediate node k
for (let k = 0; k < n; k++) {
// Check for every (i, j) pair of nodes
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
/* If k is not an intermediate
node, skip the iteration */
if (matrix[i][k] === -1 || matrix[k][j] === -1)
continue;
/* If no direct edge from
i to v is present */
if (matrix[i][j] === -1) {
// Update the distance
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
/* Else update the distance to
minimum of both paths */
else {
matrix[i][j] =
Math.min(matrix[i][j], matrix[i][k] + matrix[k][j]);
}
}
}
}
}
}
// Example usage
let matrix = [
[0, 2, -1, -1],
[1, 0, 3, -1],
[-1, -1, 0, -1],
[3, 5, 4, 0]
];
// Creating an instance of
// Solution class
let sol = new Solution();
// Function to find the shortest distance
// between every pair of vertices.
sol.shortest_distance(matrix);
// Output
console.log("The shortest distance matrix is:");
matrix.forEach(row => console.log(row.join(" ")));
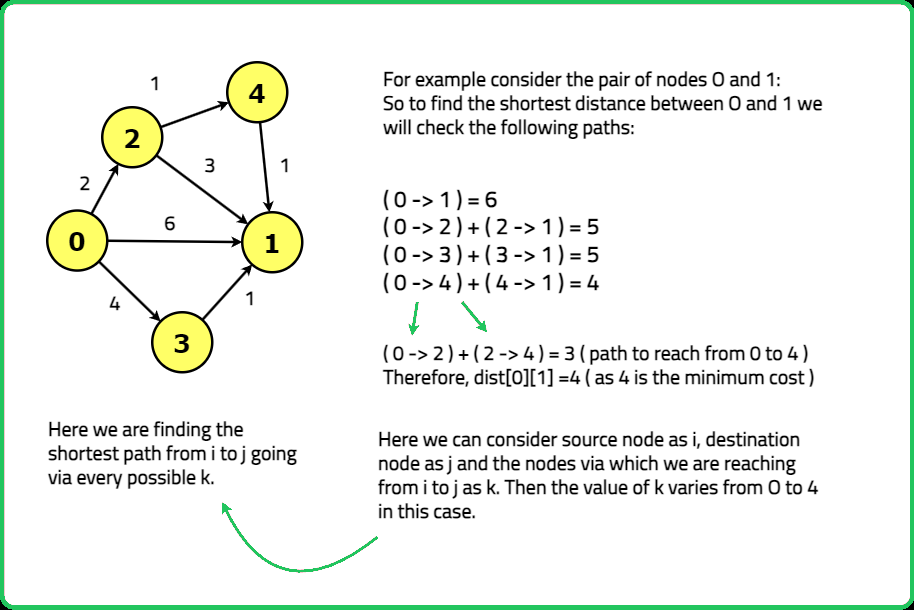where we aim to find the shortest distance from source node to destination node. The algorithm suggests to check every path (via other nodes) from source to destination node to find the required shortest distance. 
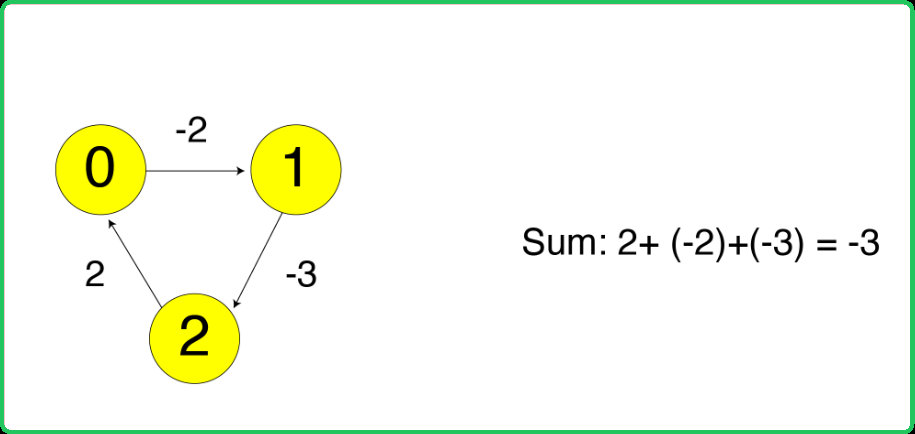Here, the distance to reach node 0 is coming out to be -3, where it should have been 0. Hence, if it is found that the distance to reach any node from itself is negative, the graph contains negative cycle.
