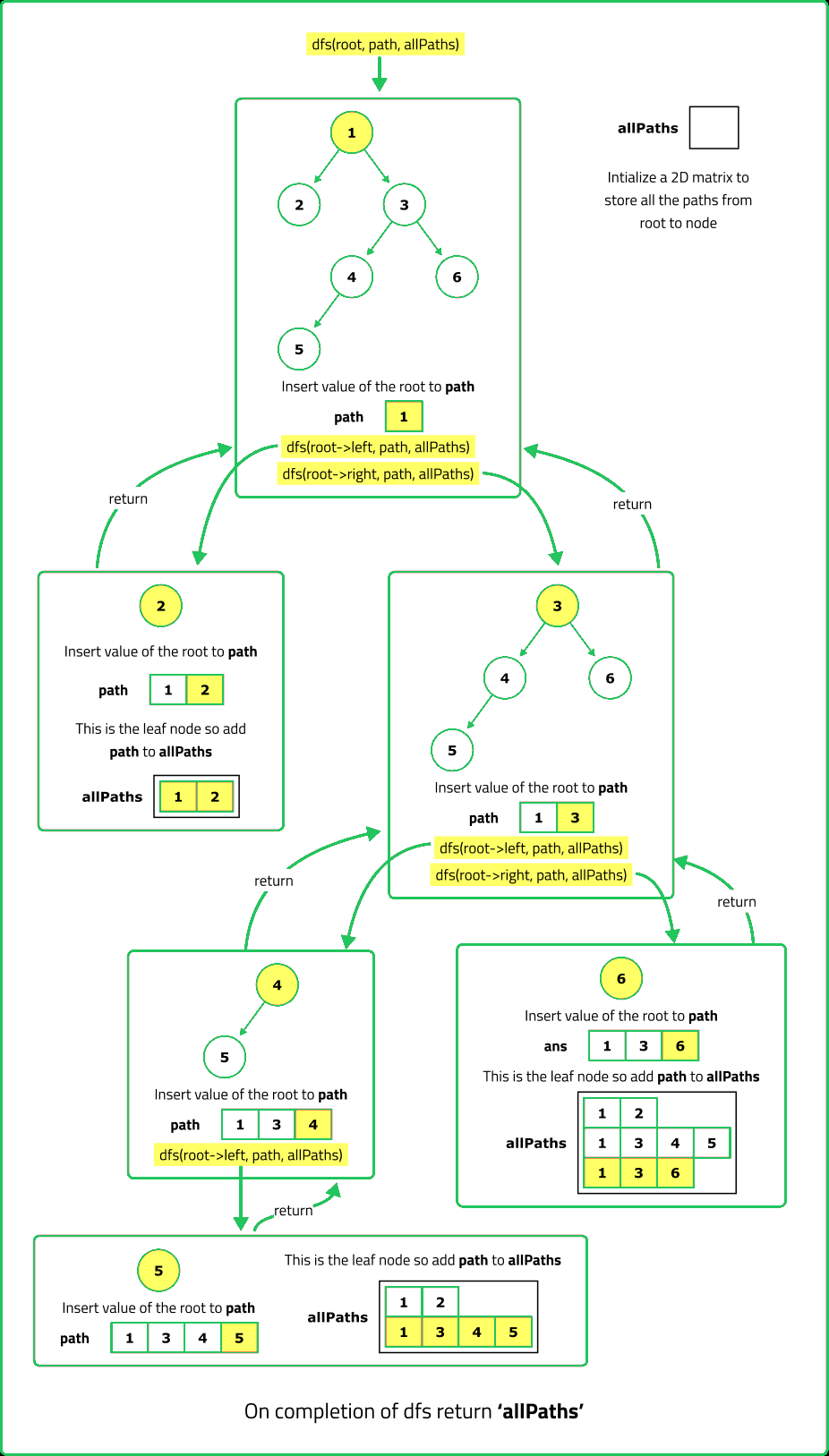
Print root to node path in BT
Binary Trees
FAQs
Hard
- This problem involves using tree traversal, which is a key component of handling structured data
- An interesting real-world application of such problems is in parsing data in XML or JSON format
- These data formats are extensively used in web and app development, APIs, and configuration files
- The tree-based structure of these formats often requires programs that can traverse their hierarchical nature, similar to the problem of finding all root-to-leaf paths in a binary tree
Given the root of a binary tree. Return all the root-to-leaf paths in the binary tree.
A leaf node of a binary tree is the node which does not have a left and right child.
Examples:
Input : root = [1, 2, 3, null, 5, null, 4]
Output : [ [1, 2, 5] , [1, 3, 4] ]
Explanation : There are only two paths from root to leaf.
From root 1 to 5 , 1 -> 2 -> 5.
From root 1 to 4 , 1 -> 3 -> 4.
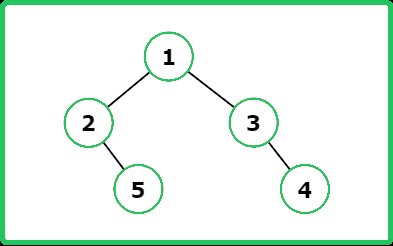
Input : root = [1, 2, 3, 4, 5]
Output : [ [1, 2, 4] , [1, 2, 5] , [1, 3] ]
Explanation :
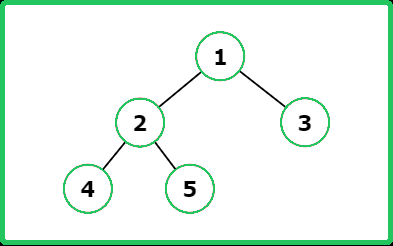
Input : root = [1, 2, 3, 4, null, 5, 6, null, 7]
Constraints
- 1 <= Number of Nodes <= 3*103
- -103 <= Node.val <= 103
Hints
- Start from the root node and traverse the tree recursively. Maintain a current path list that stores nodes visited so far.
- When reaching a leaf node, store the current path in the result list. Use backtracking to remove the last node when returning from recursion.
Company Tags
Cloudflare
Lyft
Docker
Etsy
Shopify
Boston Consulting Group
Johnson & Johnson
Bain & Company
Rakuten
Teladoc Health
Flipkart
Byju's
Chewy
Oracle
Square
Rockstar Games
Micron Technology
ARM
Walmart
Activision Blizzard
Ernst & Young
Ubisoft
Salesforce
Cerner
OYO Rooms
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe