Count subarrays with given sum
Hashing
FAQs
Hard
- Fun Fact: The underlying concept of this problem is extensively used in the development of financial software and analytical tools
- They often require fetching and calculating subarrays of financial data with a certain sum to perform risk assessment, portfolio optimization, model investment scenarios, and track financial anomalies
- It forms an integral part of the data analysis engine of these software systems
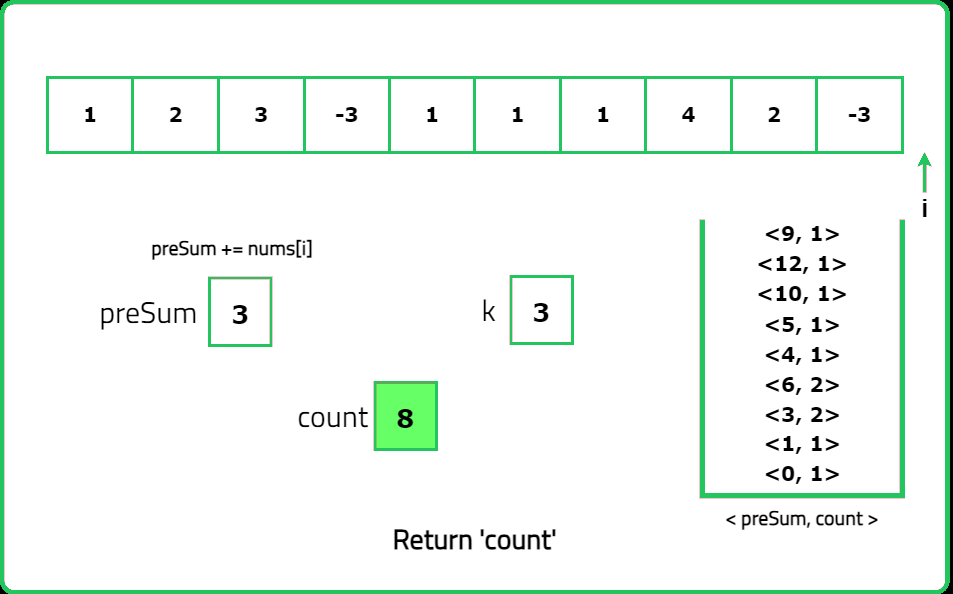
Given an array of integers nums and an integer k, return the total number of subarrays whose sum equals to k.
Examples:
Input: nums = [1, 1, 1], k = 2
Output: 2
Explanation: In the given array [1, 1, 1], there are two subarrays that sum up to 2: [1, 1] and [1, 1]. Hence, the output is 2.
Input: nums = [1, 2, 3], k = 3
Output: 2
Explanation: In the given array [1, 2, 3], there are two subarrays that sum up to 3: [1, 2] and [3]. Hence, the output is 2.
Input: nums = [3, 1, 2, 4], k = 6
Constraints
- 1 <= nums.length <= 105
- -1000 <= nums[i] <= 1000
- -107 <= k <= 107
Hints
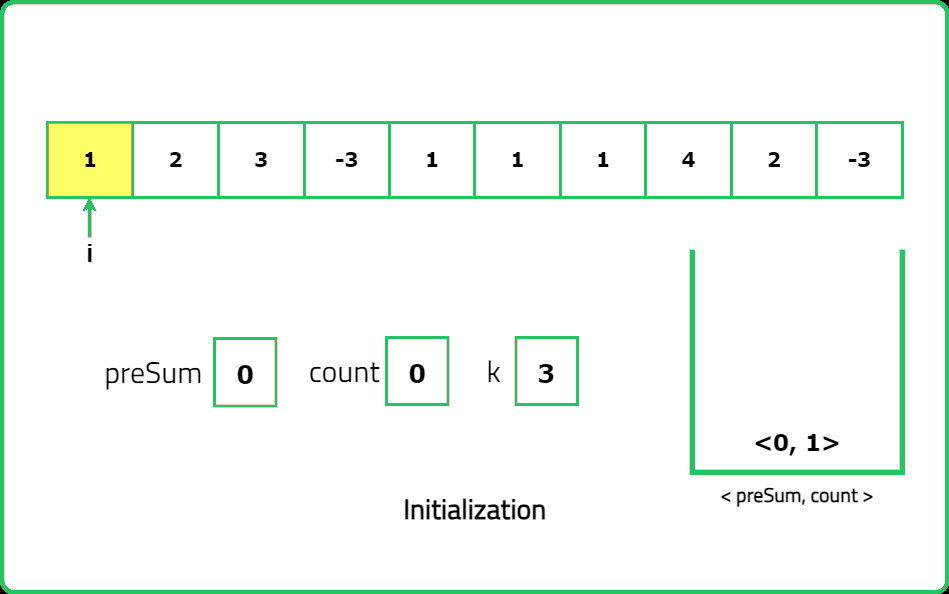
- Use a hash map to store the frequency of prefix sums encountered so far. This allows efficient calculation of the number of subarrays that sum to k.
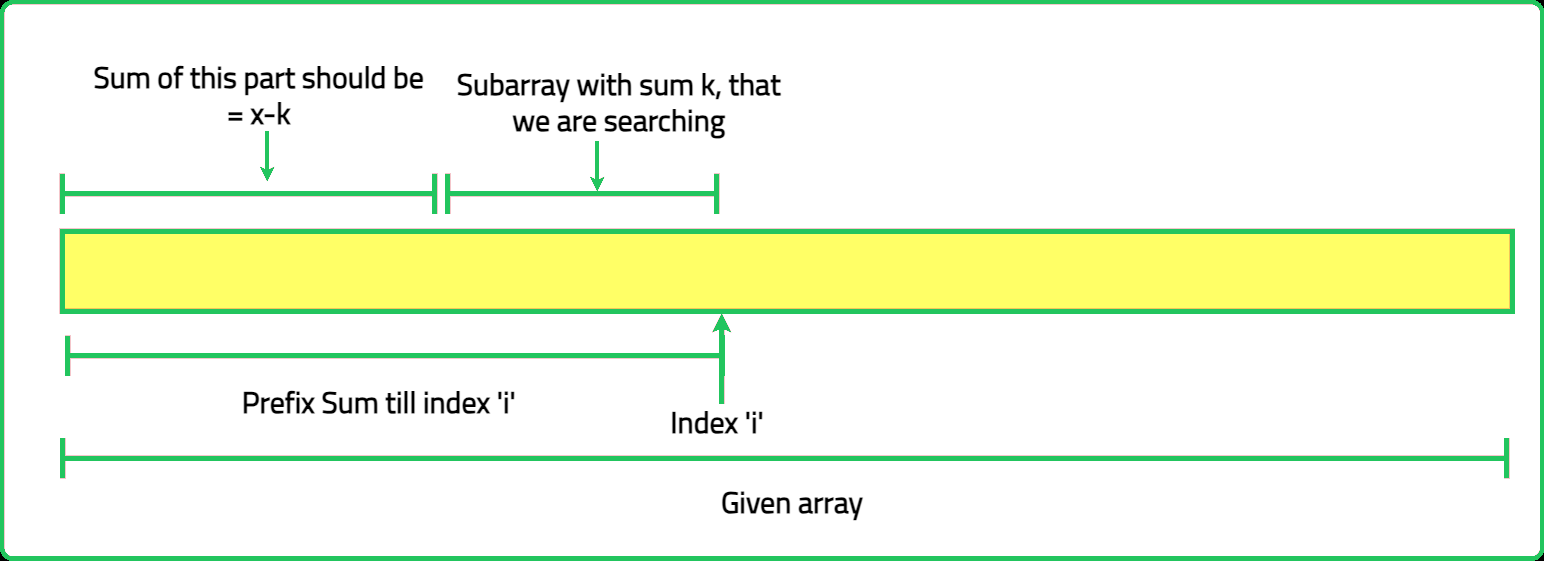
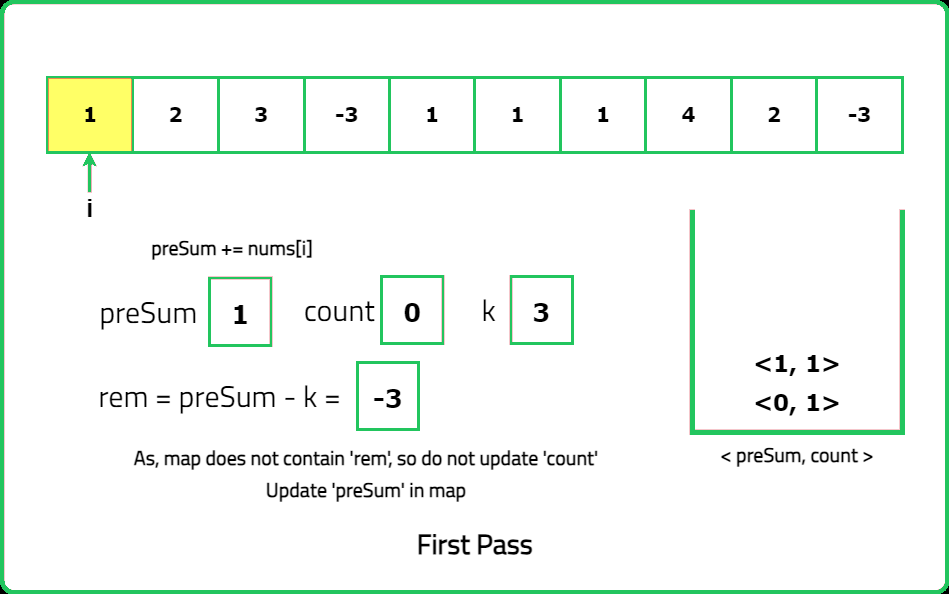
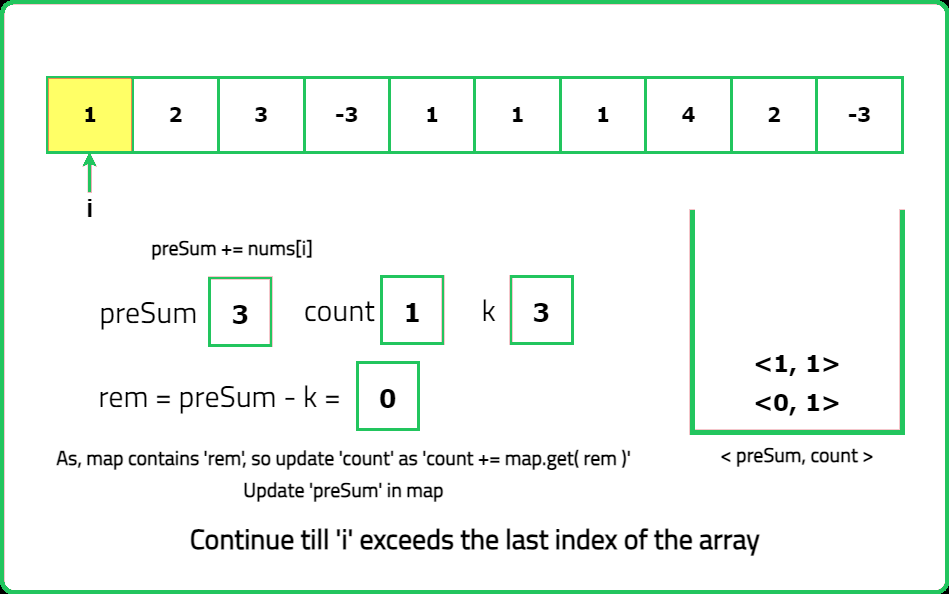
- For each index i, calculate the prefix sum up to that point. If prefixSum−k exists in the hash map, it indicates that there are subarrays ending at index i with a sum equal to k.
Company Tags
KPMG
Morgan Stanley
Rakuten
Freshworks
Byju's
HashiCorp
Cerner
Zynga
Flipkart
ARM
DoorDash
Roblox
Databricks
Uber
IBM
Instacart
Johnson & Johnson
Wayfair
Teladoc Health
Rockstar Games
Swiggy
Roche
Bungie
Medtronic
Broadcom
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe