Find the MST weight
Graphs
Minimum Spanning Tree
Hard
- Fun Fact: The concept of a Minimum Spanning Tree, as outlined in the problem statement, is a fundamental algorithm used within network design
- It plays a key role in practical applications such as the design of computer, telecommunication, and transportation networks
- In any such network, it is crucial to connect all nodes with the minimum possible cost, hence the need for an MST
- It’s also used in data clustering algorithms (like hierarchical clustering) in machine learning, and image segmentation in computer vision
Given a weighted, undirected, and connected graph with V vertices numbered from 0 to V-1 and E edges.
The ith edge is represented by [ai,bi,wi], where ai and bi denotes the endpoint of the edge and the wi denotes the weight of the edge.
Find the sum of the weights of the edges in the Minimum Spanning Tree (MST) of the graph.
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight.
Examples:
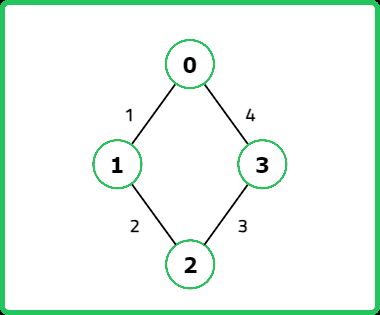
Input: V = 4, edges = [[0, 1, 1], [1, 2, 2], [2, 3, 3], [0, 3, 4]]
Output: 6
Explanation:
Edges included in the MST:
[0, 1, 1] with weight 1
[1, 2, 2] with weight 2
[2, 3, 3] with weight 3
The total weight of the MST is 1 + 2 + 3 = 6. These edges form a spanning tree that connects all vertices (0, 1, 2, 3) with the minimum possible total edge weight, satisfying the MST properties.
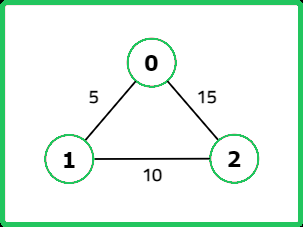
Input: V = 3, edges = [[0, 1, 5], [1, 2, 10], [2,0,15]]
Output: 15
Explanation:
Edges included in the MST:
[0, 1, 5] with weight 5
[1, 2, 10] with weight 10
The total weight of the MST is 5+10 = 15
Input: V = 4, edges = [[0, 1, 1], [1, 2, 2], [2, 3, 3], [0, 3, 4]]
Constraints
- 2 ≤ V ≤ 103
- V-1 ≤ E ≤ 104
- 1 ≤ w ≤ 105
Hints
- Sort edges in ascending order of weight. Use Disjoint Set (Union-Find with Path Compression & Union by Rank) to keep track of connected components. Iterate over sorted edges. If an edge does not form a cycle, include it in the MST and merge the components. If V-1 edges have been included, stop (MST is complete). Return the sum of MST edge weights.
- Use a priority queue (min-heap) to always expand the lightest edge connected to the MST. Maintain a visited set and a cost array to track the cheapest edge connecting each vertex to the MST. Extract the minimum-weight edge and expand the MST iteratively until all vertices are included. Return the sum of MST edge weights.
Company Tags
Wayfair
Texas Instruments
Optum
American Express
Deloitte
Bungie
Walmart
Rakuten
Docker
Instacart
Freshworks
Seagate Technology
Unity Technologies
Visa
Qualcomm
Airbnb
Micron Technology
Alibaba
Splunk
IBM
Broadcom
Square
Activision Blizzard
Philips Healthcare
Roblox
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
The minimum spanning tree consists of edges having minimum possible edge weight that are connecting all the nodes. So, a greedy approach can be followed where all the edges are considered from a node and the minimum edge is considered connecting that node. This way, it ensures that once all the nodes are visited, the edges that are taken into the consideration form a minimum spanning tree.
This is the principle behind the Prim's Algorithm to find the minimum spanning tree for a given graph.
Algorithm:
- Start with any node as the initial node in the MST. Set its key value to 0 and all other nodes' key values to infinity.
- Select the node with the minimum key value that is not yet included in the MST. Add this node to the MST.
- Update the key values of its adjacent nodes to the edge weights if the edge weight is smaller than the current key value.
- Repeat the process until all nodes are included in the MST.
- Once all the nodes are included, the MST is complete
Understanding:
Since, from every node, the minimum edge will be considered for the MST every time, the best data structure to use here will be the Minimum heap data structure, which will store a pair: {edge, node}.Approach:
- A minimum priority queue (min-heap) is used to keep track of the edges based on their weights. A visited array is used to mark nodes that have been included in the MST.
- An arbitrary initial node is pushed into the priority queue with an edge weight of 0. While the priority queue is not empty, extract the edge with the minimum weight.
- If the node connected by this edge is already visited, skip it. Otherwise, mark the node as visited and add the edge weight to the MST sum.
- Traverse all adjacent edges of the current node. For each adjacent node that is not visited, push the edge into the priority queue.
- The process continues until all nodes are included in the MST. The final sum of the weights of the edges in the MST is returned.
Dry Run:
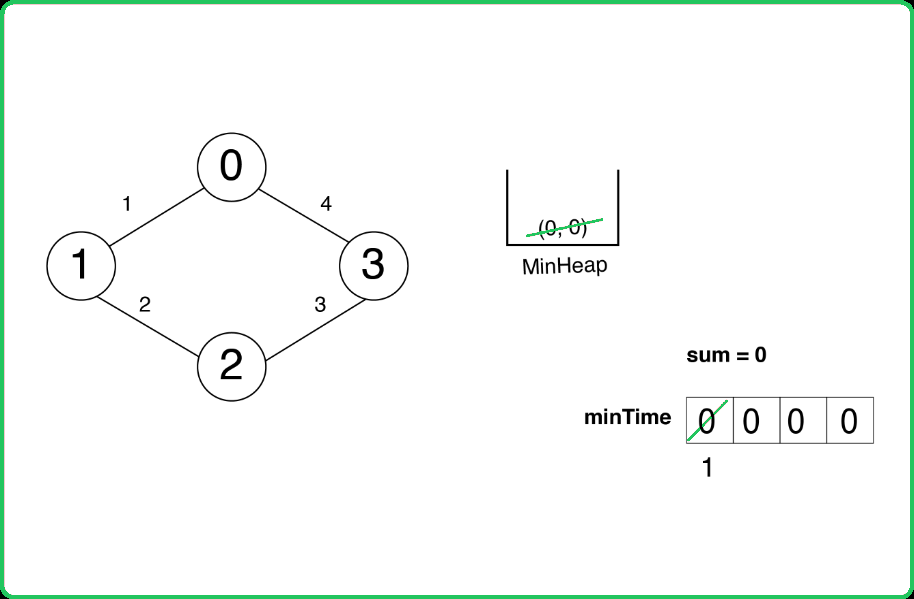
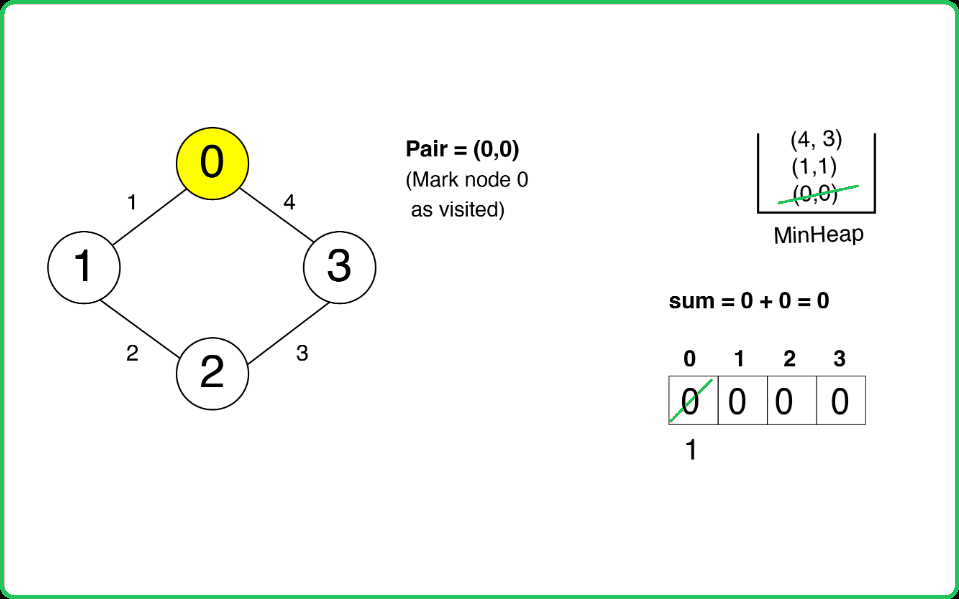
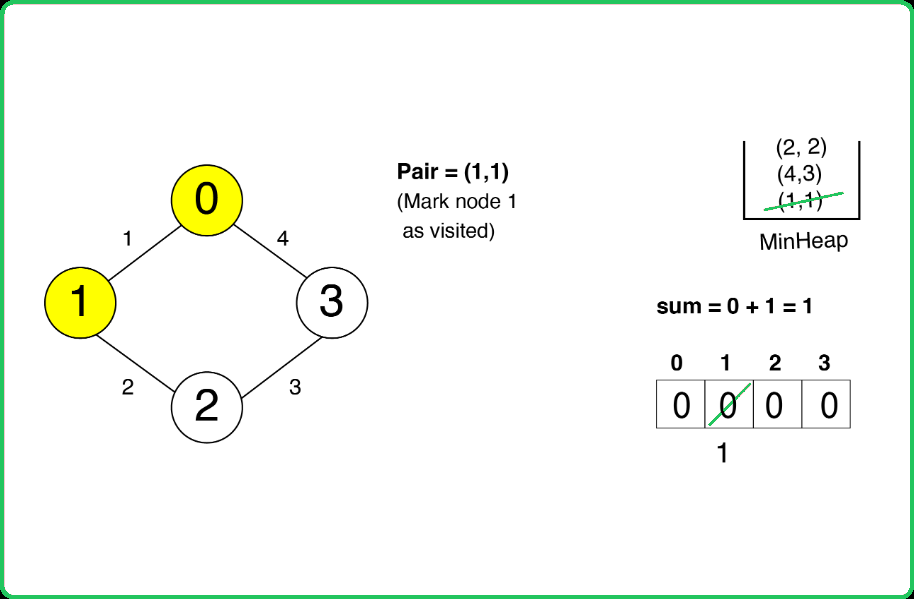
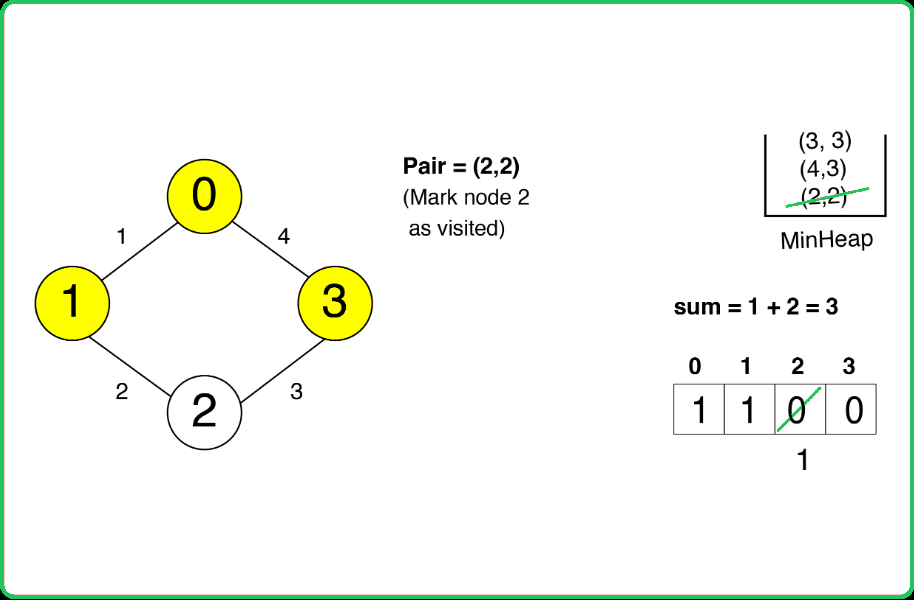
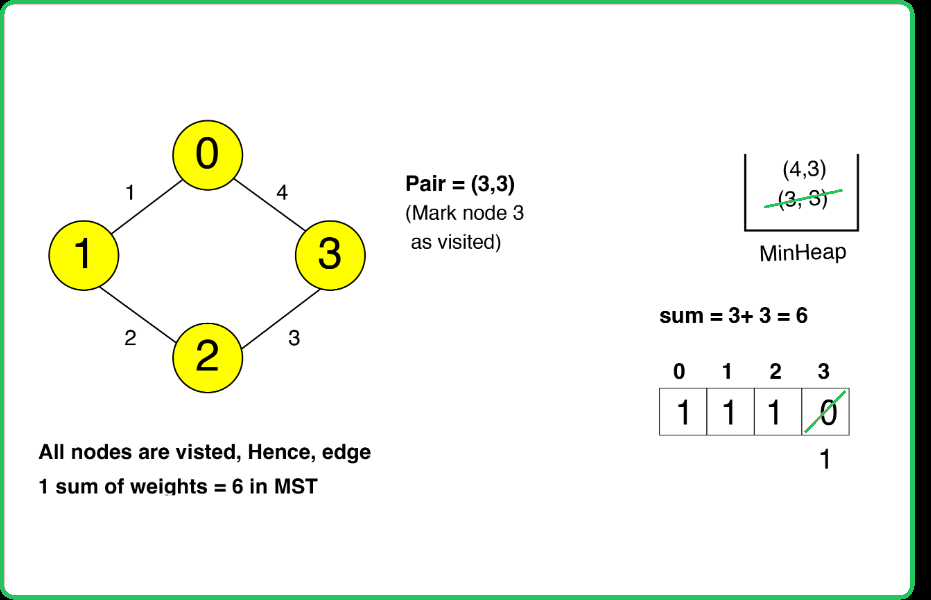
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899
#include <bits/stdc++.h>
using namespace std;
/* Define P as a shorthand for
the pair<int, pair<int,int>> type */
#define P pair<int,int>
class Solution{
public:
// Function to get the sum of weights of edges in MST
int spanningTree(int V, vector<vector<int>> adj[]) {
// Min-Heap to store pair of {edge, node}
priority_queue <P, vector<P>, greater<P>> pq;
// Visited array
vector<int> visited(V, 0);
// Push any arbitrary initial node
pq.push({0,0});
// To store the weight of MST
int sum = 0;
// Until the priority queue is not empty
while(!pq.empty()) {
// Get the pair with minimum edge
auto p = pq.top();
pq.pop();
int node = p.second; // Get the node
int wt = p.first; // Get the edge weight
/* If the node is already visited,
skip the iteration */
if(visited[node] == 1) continue;
// Otherwise, mark the node as visited
visited[node] = 1;
// Update the weight of MST
sum += wt;
// Traverse all the edges of the node
for(auto it : adj[node]) {
// Get the adjacent node
int adjNode = it[0];
// Get the edge weight
int edgeWt = it[1];
/* Add the pair to min-heap if
the node is not visited already */
if(visited[adjNode] == 0) {
pq.push({edgeWt, adjNode});
}
}
}
// Return the weight of MST
return sum;
}
};
int main() {
int V = 4;
vector<vector<int>> edges = {
{0, 1, 1},
{1, 2, 2},
{2, 3, 3},
{0, 3, 4}
};
// Forming the adjacency list from edges
vector<vector<int>> adj[4];
for(auto it : edges) {
int u = it[0];
int v = it[1];
int wt = it[2];
adj[u].push_back({v, wt});
adj[v].push_back({u, wt});
}
// Creating instance of Solution class
Solution sol;
/* Function call to get the sum
of weights of edges in MST */
int ans = sol.spanningTree(V, adj);
cout << "The sum of weights of edges in MST is: " << ans;
return 0;
}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394
import java.util.*;
public class Solution {
// Function to get the sum of weights of edges in MST
public int spanningTree(int V, List<List<List<Integer>>> adj) {
// Min-Heap to store pair of {edge, node}
PriorityQueue<int[]> pq =
new PriorityQueue<>(Comparator.comparingInt(o -> o[0]));
// Visited array
boolean[] visited = new boolean[V];
// Push any arbitrary initial node
pq.add(new int[]{0, 0});
// To store the weight of MST
int sum = 0;
// Until the priority queue is not empty
while (!pq.isEmpty()) {
// Get the pair with minimum edge
int[] p = pq.poll();
int node = p[1]; // Get the node
int wt = p[0]; // Get the edge weight
/* If the node is already visited,
skip the iteration */
if (visited[node]) continue;
// Otherwise, mark the node as visited
visited[node] = true;
// Update the weight of MST
sum += wt;
// Traverse all the edges of the node
for (List<Integer> it : adj.get(node)) {
// Get the adjacent node
int adjNode = it.get(0);
// Get the edge weight
int edgeWt = it.get(1);
/* Add the pair to min-heap if
the node is not visited already */
if (!visited[adjNode]) {
pq.add(new int[]{edgeWt, adjNode});
}
}
}
// Return the weight of MST
return sum;
}
public static void main(String[] args) {
int V = 4;
List<List<Integer>> edges = Arrays.asList(
Arrays.asList(0, 1, 1),
Arrays.asList(1, 2, 2),
Arrays.asList(2, 3, 3),
Arrays.asList(0, 3, 4)
);
// Forming the adjacency list from edges
List<List<List<Integer>>> adj = new ArrayList<>();
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
for (List<Integer> it : edges) {
int u = it.get(0);
int v = it.get(1);
int wt = it.get(2);
adj.get(u).add(Arrays.asList(v, wt));
adj.get(v).add(Arrays.asList(u, wt));
}
// Creating instance of Solution class
Solution sol = new Solution();
/* Function call to get the sum
of weights of edges in MST */
int ans = sol.spanningTree(V, adj);
System.out.println("The sum of weights of edges in MST is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677
import heapq
class Solution:
# Function to get the sum of weights of edges in MST
def spanningTree(self, V, adj):
# Min-Heap to store pair of {edge, node}
pq = []
# Visited array
visited = [0] * V
# Push any arbitrary initial node
heapq.heappush(pq, (0, 0))
# To store the weight of MST
sum = 0
# Until the priority queue is not empty
while pq:
# Get the pair with minimum edge
wt, node = heapq.heappop(pq)
# If the node is already visited,
# skip the iteration
if visited[node] == 1:
continue
# Otherwise, mark the node as visited
visited[node] = 1
# Update the weight of MST
sum += wt
# Traverse all the edges of the node
for it in adj[node]:
# Get the adjacent node
adjNode = it[0]
# Get the edge weight
edgeWt = it[1]
# Add the pair to min-heap if
# the node is not visited already
if visited[adjNode] == 0:
heapq.heappush(pq, (edgeWt, adjNode))
# Return the weight of MST
return sum
if __name__ == "__main__":
V = 4
edges = [
[0, 1, 1],
[1, 2, 2],
[2, 3, 3],
[0, 3, 4]
]
# Forming the adjacency list from edges
adj = [[] for _ in range(V)]
for it in edges:
u, v, wt = it
adj[u].append([v, wt])
adj[v].append([u, wt])
# Creating instance of Solution class
sol = Solution()
# Function call to get the sum of weights of edges in MST
ans = sol.spanningTree(V, adj)
print("The sum of weights of edges in MST is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155
// Minimum Heap Implementation
class MinHeap {
constructor() {
this.heap = [];
}
insert(key, value) {
this.heap.push({ key, value });
this.bubbleUp();
}
bubbleUp() {
let index = this.heap.length - 1;
while (index > 0) {
let element = this.heap[index];
let parentIndex = Math.floor((index - 1) / 2);
let parent = this.heap[parentIndex];
if (parent.key <= element.key) break;
this.heap[index] = parent;
this.heap[parentIndex] = element;
index = parentIndex;
}
}
extractMin() {
const min = this.heap[0];
const end = this.heap.pop();
if (this.heap.length > 0) {
this.heap[0] = end;
this.sinkDown(0);
}
return min;
}
sinkDown(index) {
const length = this.heap.length;
const element = this.heap[index];
while (true) {
let leftChildIndex = 2 * index + 1;
let rightChildIndex = 2 * index + 2;
let leftChild, rightChild;
let swap = null;
if (leftChildIndex < length) {
leftChild = this.heap[leftChildIndex];
if (leftChild.key < element.key) {
swap = leftChildIndex;
}
}
if (rightChildIndex < length) {
rightChild = this.heap[rightChildIndex];
if (
(swap === null && rightChild.key < element.key) ||
(swap !== null && rightChild.key < leftChild.key)
) {
swap = rightChildIndex;
}
}
if (swap === null) break;
this.heap[index] = this.heap[swap];
this.heap[swap] = element;
index = swap;
}
}
isEmpty() {
return this.heap.length === 0;
}
}
class Solution {
// Function to get the sum of weights of edges in MST
spanningTree(V, adj) {
// Min-Heap to store pair of {edge, node}
const pq = new MinHeap();
// Visited array
const visited = new Array(V).fill(false);
// Push any arbitrary initial node
pq.insert(0, 0);
// To store the weight of MST
let sum = 0;
// Until the priority queue is not empty
while (!pq.isEmpty()) {
// Get the pair with minimum edge
const p = pq.extractMin();
const node = p.value; // Get the node
const wt = p.key; // Get the edge weight
/* If the node is already visited,
skip the iteration */
if (visited[node]) continue;
// Otherwise, mark the node as visited
visited[node] = true;
// Update the weight of MST
sum += wt;
// Traverse all the edges of the node
adj[node].forEach(it => {
// Get the adjacent node
const adjNode = it[0];
// Get the edge weight
const edgeWt = it[1];
/* Add the pair to min-heap if
the node is not visited already */
if (!visited[adjNode]) {
pq.insert(edgeWt, adjNode);
}
});
}
// Return the weight of MST
return sum;
}
}
const V = 4;
const edges = [
[0, 1, 1],
[1, 2, 2],
[2, 3, 3],
[0, 3, 4]
];
// Forming the adjacency list from edges
const adj = Array.from({ length: V }, () => []);
edges.forEach(it => {
const [u, v, wt] = it;
adj[u].push([v, wt]);
adj[v].push([u, wt]);
});
// Creating instance of Solution class
const sol = new Solution();
/* Function call to get the sum
of weights of edges in MST */
const ans = sol.spanningTree(V, adj);
console.log("The sum of weights of edges in MST is:", ans);
Complexity Analysis:
Time Complexity: O(ElogE) (where E is the number of edges in the graph)
In the worst case, the min-heap will store all the E edges, and insertion operation on the min-heap takes O(logE) time taking overall O(ElogE) time.
Space Complexity: O(E + V) (where V is the number of nodes in the graph)
The min-heap will store all edges in worst-case taking O(E) space and the visited array takes O(V) space.
Intuition:
Since, the minimum spanning tree consists of edges connecting all nodes with the minimum total weight, a greedy approach can be followed where the edges with the smallest edge weight can be added to the MST set one by one till all the nodes are not added to the MST.
Algorithm:
- Sort all the edges in ascending order based on their weights. Initialize the total weight sum to 0.
- Initialize a data structure to keep track of connected components (e.g., union-find).
- Iterate through the sorted edges:
- For each edge, check if the vertices it connects are in different components.
- If they are in different components, add the edge's weight to the total weight sum and unite the components.
- Continue this process until all vertices are connected or all edges have been processed.
Approach:
- A Disjoint Set class is created to manage the union-find operations. This class supports union by rank and union by size to efficiently manage the merging of sets.
- All edges from the adjacency list representation of the graph are extracted and stored in a list, with each edge represented as a pair of its weight and the two vertices it connects.
- The list of edges is sorted in ascending order based on their weights. This ensures that the smallest edges are considered first, which is a key aspect of Kruskal's algorithm.
- A variable is initialized to keep track of the sum of the weights of the edges included in the MST.
- Iterate through the sorted list of edges. For each edge, check if the two vertices connected by the edge belong to different sets using the union-find structure. If they do, add the edge's weight to the MST sum and merge the sets containing these two vertices.
- After processing all edges, the sum of the weights of the edges in the MST is returned.
Dry Run:
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144
#include <bits/stdc++.h>
using namespace std;
class DisjointSet {
/* To store the ranks, parents and
sizes of different set of vertices */
vector<int> rank, parent, size;
public:
// Constructor
DisjointSet(int n) {
rank.resize(n + 1, 0);
parent.resize(n + 1);
size.resize(n + 1);
for (int i = 0; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// Function to find ultimate parent
int findUPar(int node) {
if (node == parent[node])
return node;
return parent[node] = findUPar(parent[node]);
}
// Function to implement union by rank
void unionByRank(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (rank[ulp_u] < rank[ulp_v]) {
parent[ulp_u] = ulp_v;
}
else if (rank[ulp_v] < rank[ulp_u]) {
parent[ulp_v] = ulp_u;
}
else {
parent[ulp_v] = ulp_u;
rank[ulp_u]++;
}
}
// Function to implement union by size
void unionBySize(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (size[ulp_u] < size[ulp_v]) {
parent[ulp_u] = ulp_v;
size[ulp_v] += size[ulp_u];
}
else {
parent[ulp_v] = ulp_u;
size[ulp_u] += size[ulp_v];
}
}
};
// Solution class
class Solution{
public:
// Function to get the sum of weights of edges in MST
int spanningTree(int V, vector<vector<int>> adj[]) {
// To store the edges
vector<pair<int, pair<int, int>>> edges;
// Getting all edges from adjacency list
for (int i = 0; i < V; i++) {
for (auto it : adj[i]) {
int v = it[0]; // Node v
int wt = it[1]; // edge weight
int u = i; // Node u
edges.push_back({wt, {u, v}});
}
}
// Creating a disjoint set of V vertices
DisjointSet ds(V);
// Sorting the edges based on their weights
sort(edges.begin(), edges.end());
// To store the sum of edges in MST
int sum = 0;
// Iterate on the edges
for (auto it : edges) {
int wt = it.first; // edge weight
int u = it.second.first; // First node
int v = it.second.second; // Second node
// Join the nodes if not in the same set
if (ds.findUPar(u) != ds.findUPar(v)) {
// Update the sum of edges in MST
sum += wt;
// Unite the nodes
ds.unionBySize(u, v);
}
}
// Return the computed sum
return sum;
}
};
int main() {
int V = 4;
vector<vector<int>> edges = {
{0, 1, 1},
{1, 2, 2},
{2, 3, 3},
{0, 3, 4}
};
// Forming the adjacency list from edges
vector<vector<int>> adj[4];
for(auto it : edges) {
int u = it[0];
int v = it[1];
int wt = it[2];
adj[u].push_back({v, wt});
adj[v].push_back({u, wt});
}
// Creating instance of Solution class
Solution sol;
/* Function call to get the sum
of weights of edges in MST */
int ans = sol.spanningTree(V, adj);
cout << "The sum of weights of edges in MST is: " << ans;
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142
import java.util.*;
class DisjointSet {
/* To store the ranks, parents and
sizes of different set of vertices */
List<Integer> rank, parent, size;
// Constructor
public DisjointSet(int n) {
rank = new ArrayList<>(n + 1);
Collections.fill(rank, 0);
parent = new ArrayList<>(n + 1);
size = new ArrayList<>(n + 1);
for (int i = 0; i <= n; i++) {
parent.add(i);
size.add(1);
}
}
// Function to find ultimate parent
public int findUPar(int node) {
if (node == parent.get(node))
return node;
parent.set(node, findUPar(parent.get(node)));
return parent.get(node);
}
// Function to implement union by rank
public void unionByRank(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (rank.get(ulp_u) < rank.get(ulp_v)) {
parent.set(ulp_u, ulp_v);
}
else if (rank.get(ulp_v) < rank.get(ulp_u)) {
parent.set(ulp_v, ulp_u);
}
else {
parent.set(ulp_v, ulp_u);
rank.set(ulp_u, rank.get(ulp_u) + 1);
}
}
// Function to implement union by size
public void unionBySize(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (size.get(ulp_u) < size.get(ulp_v)) {
parent.set(ulp_u, ulp_v);
size.set(ulp_v, size.get(ulp_v) + size.get(ulp_u));
}
else {
parent.set(ulp_v, ulp_u);
size.set(ulp_u, size.get(ulp_u) + size.get(ulp_v));
}
}
}
// Solution class
class Solution {
// Function to get the sum of weights of edges in MST
public int spanningTree(int V, List<List<List<Integer>>> adj) {
// To store the edges
List<int[]> edges = new ArrayList<>();
// Getting all edges from adjacency list
for (int i = 0; i < V; i++) {
for (List<Integer> it : adj.get(i)) {
int v = it.get(0); // Node v
int wt = it.get(1); // edge weight
int u = i; // Node u
edges.add(new int[]{wt, u, v});
}
}
// Creating a disjoint set of V vertices
DisjointSet ds = new DisjointSet(V);
// Sorting the edges based on their weights
edges.sort(Comparator.comparingInt(o -> o[0]));
// To store the sum of edges in MST
int sum = 0;
// Iterate on the edges
for (int[] it : edges) {
int wt = it[0]; // edge weight
int u = it[1]; // First node
int v = it[2]; // Second node
// Join the nodes if not in the same set
if (ds.findUPar(u) != ds.findUPar(v)) {
// Update the sum of edges in MST
sum += wt;
// Unite the nodes
ds.unionBySize(u, v);
}
}
// Return the computed sum
return sum;
}
public static void main(String[] args) {
int V = 4;
List<int[]> edges = Arrays.asList(
new int[]{0, 1, 1},
new int[]{1, 2, 2},
new int[]{2, 3, 3},
new int[]{0, 3, 4}
);
// Forming the adjacency list from edges
List<List<List<Integer>>> adj = new ArrayList<>(V);
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
for (int[] it : edges) {
int u = it[0];
int v = it[1];
int wt = it[2];
adj.get(u).add(Arrays.asList(v, wt));
adj.get(v).add(Arrays.asList(u, wt));
}
// Creating instance of Solution class
Solution sol = new Solution();
/* Function call to get the sum
of weights of edges in MST */
int ans = sol.spanningTree(V, adj);
System.out.println("The sum of weights of edges in MST is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108
class DisjointSet:
# To store the ranks, parents and sizes
# of different set of vertices
def __init__(self, n):
self.rank = [0] * (n + 1)
self.parent = list(range(n + 1))
self.size = [1] * (n + 1)
# Function to find ultimate parent
def findUPar(self, node):
if node == self.parent[node]:
return node
self.parent[node] = self.findUPar(self.parent[node])
return self.parent[node]
# Function to implement union by rank
def unionByRank(self, u, v):
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
if ulp_u == ulp_v:
return
if self.rank[ulp_u] < self.rank[ulp_v]:
self.parent[ulp_u] = ulp_v
elif self.rank[ulp_v] < self.rank[ulp_u]:
self.parent[ulp_v] = ulp_u
else:
self.parent[ulp_v] = ulp_u
self.rank[ulp_u] += 1
# Function to implement union by size
def unionBySize(self, u, v):
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
if ulp_u == ulp_v:
return
if self.size[ulp_u] < self.size[ulp_v]:
self.parent[ulp_u] = ulp_v
self.size[ulp_v] += self.size[ulp_u]
else:
self.parent[ulp_v] = ulp_u
self.size[ulp_u] += self.size[ulp_v]
# Solution class
class Solution:
# Function to get the sum of weights of edges in MST
def spanningTree(self, V, adj):
# To store the edges
edges = []
# Getting all edges from adjacency list
for i in range(V):
for it in adj[i]:
v = it[0] # Node v
wt = it[1] # edge weight
u = i # Node u
edges.append((wt, u, v))
# Creating a disjoint set of V vertices
ds = DisjointSet(V)
# Sorting the edges based on their weights
edges.sort()
# To store the sum of edges in MST
sum = 0
# Iterate on the edges
for wt, u, v in edges:
# Join the nodes if not in the same set
if ds.findUPar(u) != ds.findUPar(v):
# Update the sum of edges in MST
sum += wt
# Unite the nodes
ds.unionBySize(u, v)
# Return the computed sum
return sum
if __name__ == "__main__":
V = 4
edges = [
[0, 1, 1],
[1, 2, 2],
[2, 3, 3],
[0, 3, 4]
]
# Forming the adjacency list from edges
adj = [[] for _ in range(V)]
for it in edges:
u = it[0]
v = it[1]
wt = it[2]
adj[u].append([v, wt])
adj[v].append([u, wt])
# Creating instance of Solution class
sol = Solution()
# Function call to get the sum of weights of edges in MST
ans = sol.spanningTree(V, adj)
print("The sum of weights of edges in MST is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131
class DisjointSet {
/* To store the ranks, parents and
sizes of different set of vertices */
constructor(n) {
this.rank = Array(n + 1).fill(0);
this.parent = Array.from(
{length: n + 1},
(_, i) => i
);
this.size = Array(n + 1).fill(1);
}
// Function to find ultimate parent
findUPar(node) {
if (node === this.parent[node])
return node;
return this.parent[node] =
this.findUPar(this.parent[node]);
}
// Function to implement union by rank
unionByRank(u, v) {
const ulp_u = this.findUPar(u);
const ulp_v = this.findUPar(v);
if (ulp_u === ulp_v) return;
if (this.rank[ulp_u] < this.rank[ulp_v]) {
this.parent[ulp_u] = ulp_v;
} else if (this.rank[ulp_v] < this.rank[ulp_u]) {
this.parent[ulp_v] = ulp_u;
} else {
this.parent[ulp_v] = ulp_u;
this.rank[ulp_u]++;
}
}
// Function to implement union by size
unionBySize(u, v) {
const ulp_u = this.findUPar(u);
const ulp_v = this.findUPar(v);
if (ulp_u === ulp_v) return;
if (this.size[ulp_u] < this.size[ulp_v]) {
this.parent[ulp_u] = ulp_v;
this.size[ulp_v] += this.size[ulp_u];
} else {
this.parent[ulp_v] = ulp_u;
this.size[ulp_u] += this.size[ulp_v];
}
}
}
// Solution class
class Solution {
// Function to get the sum of weights of edges in MST
spanningTree(V, adj) {
// To store the edges
const edges = [];
// Getting all edges from adjacency list
for (let i = 0; i < V; i++) {
for (const it of adj[i]) {
const v = it[0]; // Node v
const wt = it[1]; // edge weight
const u = i; // Node u
edges.push([wt, u, v]);
}
}
// Creating a disjoint set of V vertices
const ds = new DisjointSet(V);
// Sorting the edges based on their weights
edges.sort((a, b) => a[0] - b[0]);
// To store the sum of edges in MST
let sum = 0;
// Iterate on the edges
for (const it of edges) {
const wt = it[0]; // edge weight
const u = it[1]; // First node
const v = it[2]; // Second node
// Join the nodes if not in the same set
if (ds.findUPar(u) !== ds.findUPar(v)) {
// Update the sum of edges in MST
sum += wt;
// Unite the nodes
ds.unionBySize(u, v);
}
}
// Return the computed sum
return sum;
}
}
const main = () => {
const V = 4;
const edges = [
[0, 1, 1],
[1, 2, 2],
[2, 3, 3],
[0, 3, 4]
];
// Forming the adjacency list from edges
const adj = Array.from({length: V}, () => []);
for (const it of edges) {
const u = it[0];
const v = it[1];
const wt = it[2];
adj[u].push([v, wt]);
adj[v].push([u, wt]);
}
// Creating instance of Solution class
const sol = new Solution();
/* Function call to get the sum of
weights of edges in MST */
const ans = sol.spanningTree(V, adj);
console.log("The sum of weights of edges in MST is:", ans);
}
main();
Complexity Analysis:
Time Complexity: O(V+E) + O(ElogE) + O(E*4α*2) (where V and E are the numbers of nodes and edges in the graph)
- Extracting edges from adjacency list takes O(V+E) time.
- Sorting the edges takes O(ElogE) time.
- In the worst case, all the edges are iterated and added to the disjoint set. The find parent and union operation takes 4α time making overall time complexity as O(E*4α*2).
Space Complexity: O(V+E)
- Storing the edges take O(E) space.
- The disjoint set on V vertices take O(V) space due to parent, rank/size arrays.
Frequently Occurring Doubts
Q: What if multiple MSTs exist?
A: If weights are not unique, multiple valid MSTs can exist, but their total weight is always the same.
Q: Why does an MST always have exactly V-1 edges?
A: A tree with V nodes always has V-1 edges, ensuring minimal connectivity without cycles.
Interview Followup Questions
Q: How would we modify the algorithm to return the actual MST edges, not just the weight sum?
A: Store edges in a result list during MST construction.
Q: What if the graph had negative weights?
A: MST algorithms work even with negative weights as long as the graph is connected.
Notes
Code
✅ Testcase
Input: {'V': '4', 'edges': '[[0, 1, 1], [1, 2, 2], [2, 3, 3], [0, 3, 4]]'}
Expected:
6
6
Actual: -
Time: -
sec
Status: Waiting
Input: {'V': '3', 'edges': ' [[0, 1, 5], [1, 2, 10], [2,0,15]]'}
Expected:
15
15
Actual: -
Time: -
sec
Status: Waiting
Input: {'V': '4', 'edges': ' [[0, 1, 1], [1, 2, 2], [2, 3, 3], [0, 3, 4]]'}
Expected:
6
6
Actual: -
Time: -
sec
Status: Waiting