Power Set

Power Set

Recursion Implementation Problems Easy

The problem of finding all possible subsets from a set, also known as the power set, is an important concept in many areas of software development
In database technologies, such as SQL, this concept is used in designing queries that require combinations of data, such as generating all combinations of products that can be bundled together
In Machine Learning, power sets are used in feature selection, where combinations of different features are tested to see which set gives the best predictive accuracy
Meanwhile in Software Testing, generating all possible subsets of a feature set aids in creating exhaustive test cases which helps find potential bugs or issues

Given an array of integers nums of unique elements. Return all possible subsets (power set) of the array.

Do not include the duplicates in the answer.

Examples:

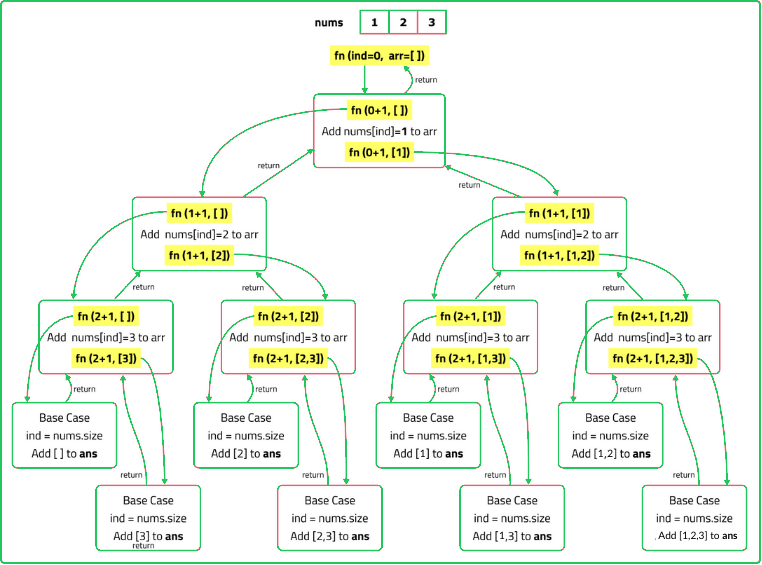
Input : nums = [1, 2, 3]

Output : [ [ ] , [1] , [2] , [1, 2] , [3] , [1, 3] , [2, 3] , [1, 2 ,3] ]

Input : nums = [1, 2]

Output : [ [ ] , [1] , [2] , [1,2] ]

Input : nums = [0]

Constraints

1 <= nums.length <= 10
-10 <= nums[i] <= 10

Hints

Use recursion to build subsets by deciding for each element whether to include it in the current subset.
"At each recursive step: Add the current subset to the result. Recursively add subsets including the next element."

Company Tags

Wayfair Dropbox Red Hat Swiggy Bain & Company Roche Zynga Nutanix Morgan Stanley Freshworks Visa MongoDB Seagate Technology Bloomberg Bungie Optum Boston Consulting Group Micron Technology Splunk HCL Technologies Activision Blizzard DoorDash Philips Healthcare Riot Games JPMorgan Chase TCS Cognizant Accenture Infosys Capgemini Wipro

Editorial

Real life Example

To understand the approach to solving the problem better let us compare this to a real-life example. Given a set of items (e.g., fruits), generate all possible combinations. Start with an empty basket. For each item, decide whether to exclude or include it in the basket, then move to the next item. When all items are considered, record the current combination. Revert to the previous step by removing the last included item and explore other combinations. This recursive process covers all possible subsets.

Intuition

Following up from the example above, to generate all possible subsets (power set) of a given set of items, start with an empty combination. For each item, decide whether to include it or not, and move to the next item. Once all items are considered, add the current combination to the list of subsets. Go back by removing the last item and explore other combinations. This recursive process ensures that all combinations are explored and recorded.

Dry Run

Approach

Base Case: When the current index equals the length of the array, it means all items have been considered. At this point, add the current subset (combination of included items) to the result list.
Make a recursive call to the function without adding the current item to the subset. This explores the possibility of subsets that do not include the current item.
Add the current item to the subset and make a recursive call to the function to explore subsets that include this item.
Backtrack: After exploring the subsets that include the current item, remove it from the subset (backtrack) and continue exploring subsets with the next items. This step ensures that all combinations are considered.
Continue the process recursively for each item, using both inclusion and exclusion to cover all possible subsets until all combinations are generated.

Solution

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    void func(int ind, int n, vector<int> &nums, vector<int> &arr, vector<vector<int>> &ans) {
        // Base case: if the index reaches the length of the array,
        // add the current subset to the answer list
        if (ind == n) {
            ans.push_back(arr);
            return;
        }

        // Recursive case: Exclude the current element and move to the next element
        func(ind + 1, n, nums, arr, ans);

        // Include the current element in the subset and move to the next element
        arr.push_back(nums[ind]);
        func(ind + 1, n, nums, arr, ans);

        // Backtrack: remove the last added element to explore other subsets
        arr.pop_back();
    }

public:
    vector<vector<int>> powerSet(vector<int> &nums) {
        vector<vector<int>> ans;  // List to store all subsets
        vector<int> arr;  // Temporary list to store the current subset
        func(0, nums.size(), nums, arr, ans);  // Start the recursive process
        return ans;  // Return the list of all subsets
    }
};

// Main method to test the code
int main() {
    Solution sol;
    vector<int> nums = {1, 2, 3};
    vector<vector<int>> result = sol.powerSet(nums);
    
    // Print the result
    for (const auto &subset : result) {
        cout << "[";
        for (int num : subset) {
            cout << num << " ";
        }
        cout << "]" << endl;
    }

    return 0;
}
import java.util.ArrayList;
import java.util.List;

class Solution {

    // Helper function to generate all subsets
    private void backtrack(int index, int n, int[] nums, List<Integer> current, List<List<Integer>> ans) {
        // Base case: if the index reaches the length of the array,
        // add the current subset to the answer list
        if (index == n) {
            ans.add(new ArrayList<>(current));
            return;
        }

        // Recursive case: Exclude the current element and move to the next element
        backtrack(index + 1, n, nums, current, ans);

        // Include the current element in the subset and move to the next element
        current.add(nums[index]);
        backtrack(index + 1, n, nums, current, ans);

        // Backtrack: remove the last added element to explore other subsets
        current.remove(current.size() - 1);
    }

    // Main function to generate the power set of the given array
    public List<List<Integer>> powerSet(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();  // List to store all subsets
        List<Integer> current = new ArrayList<>();  // Temporary list to store the current subset
        backtrack(0, nums.length, nums, current, ans);  // Start the recursive process
        return ans;  // Return the list of all subsets
    }

    // Main method to test the code
    public static void main(String[] args) {
        Solution sol = new Solution();
        int[] nums = {1, 2, 3};
        List<List<Integer>> result = sol.powerSet(nums);

        // Print the result
        for (List<Integer> subset : result) {
            System.out.println(subset);
        }
    }
}
class Solution:
    def backtrack(self, index, n, nums, current, ans):
        # Base case: if the index reaches the length of the array,
        # add the current subset to the answer list
        if index == n:
            ans.append(current[:])  # Add a copy of the current list
            return
        
        # Recursive case: Exclude the current element and move to the next element
        self.backtrack(index + 1, n, nums, current, ans)
        
        # Include the current element in the subset and move to the next element
        current.append(nums[index])
        self.backtrack(index + 1, n, nums, current, ans)
        
        # Backtrack: remove the last added element to explore other subsets
        current.pop()

    def powerSet(self, nums):
        ans = []  # List to store all subsets
        current = []  # Temporary list to store the current subset
        self.backtrack(0, len(nums), nums, current, ans)  # Start the recursive process
        return ans  # Return the list of all subsets

# Main method to test the code
if __name__ == "__main__":
    sol = Solution()
    nums = [1, 2, 3]
    print(sol.powerSet(nums))  # Expected output: [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
class Solution {
    // Helper function to generate all subsets
    backtrack(index, n, nums, current, ans) {
        // Base case: if the index reaches the length of the array,
        // add the current subset to the answer list
        if (index === n) {
            ans.push([...current]);  // Add a copy of the current list
            return;
        }

        // Recursive case: Exclude the current element and move to the next element
        this.backtrack(index + 1, n, nums, current, ans);

        // Include the current element in the subset and move to the next element
        current.push(nums[index]);
        this.backtrack(index + 1, n, nums, current, ans);

        // Backtrack: remove the last added element to explore other subsets
        current.pop();
    }

    // Main function to generate the power set of the given array
    powerSet(nums) {
        const ans = [];  // List to store all subsets
        const current = [];  // Temporary list to store the current subset
        this.backtrack(0, nums.length, nums, current, ans);  // Start the recursive process
        return ans;  // Return the list of all subsets
    }
}

// Main method to test the code
const sol = new Solution();
const nums = [1, 2, 3];
console.log(sol.powerSet(nums));  
// Expected output: [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

Time Complexity

Time Complexity O(2^N): Each element in the array has two choices: either to be included in a subset or not, leading to 2^n possible subsets.

Space Complexity O(N * 2^N): We generate 2^n subsets, and each subset can have up to n elements. Additionally, the recursion stack can go up to a depth of n.

Code

Problem List