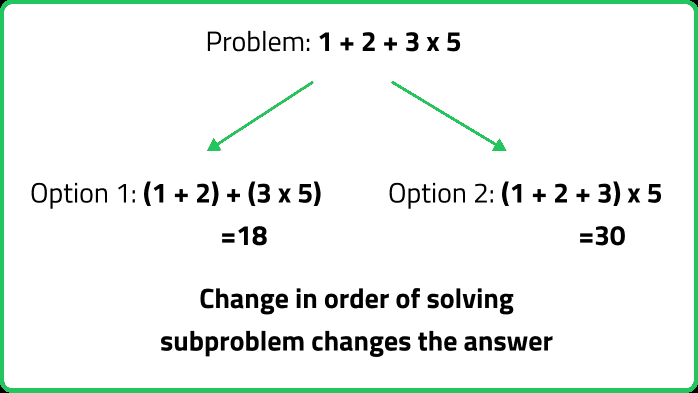
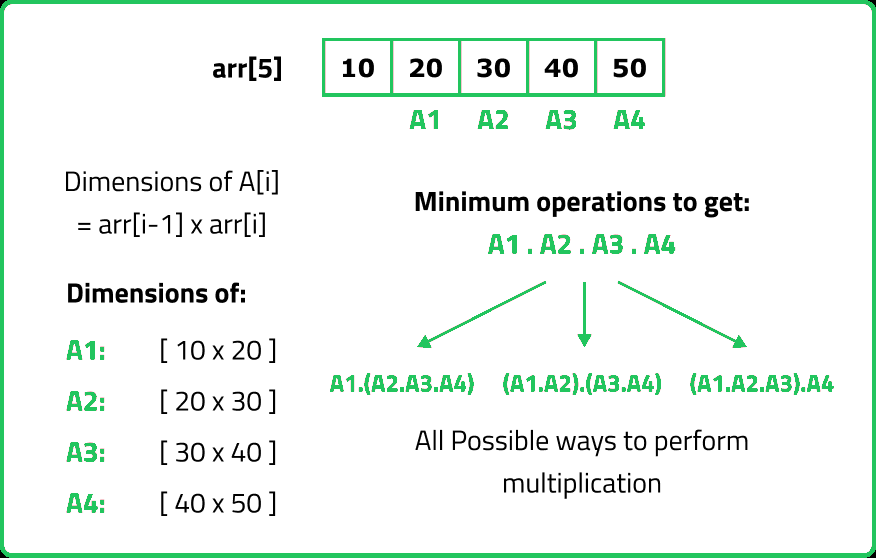
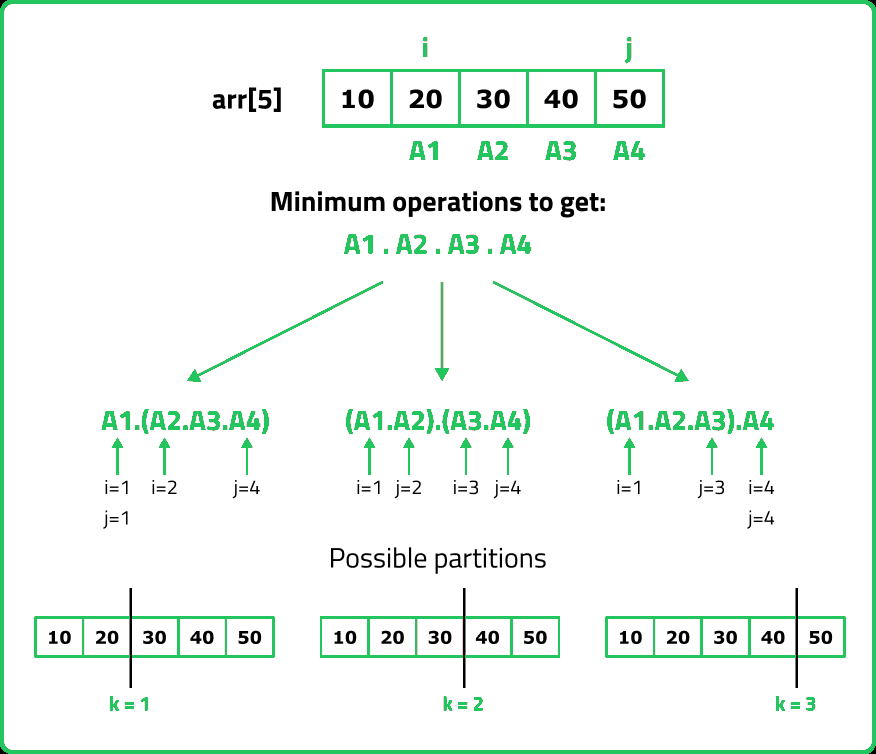
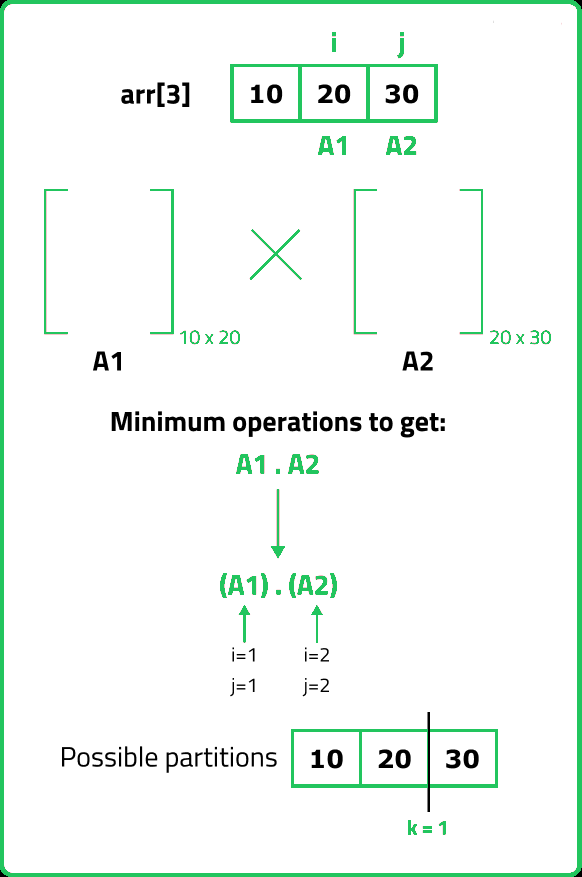
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Recursive function to compute the
minimum cost of matrix multiplication*/
int func(vector<int>& arr, int i, int j, vector<vector<int>>& dp) {
/* Base case: When there is only one
matrix, no multiplication is needed*/
if (i == j)
return 0;
//Check if the subproblem is already calculated
if(dp[i][j]!=-1)
return dp[i][j];
int mini = INT_MAX;
// Partition the matrices between i and j
for (int k = i; k <= j - 1; k++) {
/* Compute the cost of multiplying matrices
from i to k and from k+1 to j and add cost
of multiplying the two resulting matrices*/
int ans = func(arr, i, k, dp) + func(arr, k + 1, j, dp) + arr[i - 1] * arr[k] * arr[j];
// Update the minimum cost
mini = min(mini, ans);
}
// Store and return the minimum cost found
return dp[i][j] = mini;
}
public:
/* Function to set up the parameters
and call the recursive function*/
int matrixMultiplication(vector<int>& nums) {
int N = nums.size();
// Starting index of the matrix chain
int i = 1;
// Ending index of the matrix chain
int j = N - 1;
vector<vector<int>> dp(N,vector<int>(N,-1));
// Call the recursive function
return func(nums, i, j, dp);
}
};
int main() {
vector<int> arr = {10, 20, 30, 40, 50};
//Create an instance of Solution class
Solution sol;
// Print the result
cout << "The minimum number of operations is " << sol.matrixMultiplication(arr);
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
import java.util.*;
class Solution {
/* Recursive function to compute the
minimum cost of matrix multiplication*/
private int func(int[] arr, int i, int j, int[][] dp) {
/* Base case: When there is only one
matrix, no multiplication is needed*/
if (i == j)
return 0;
// Check if the subproblem is already calculated
if (dp[i][j] != -1)
return dp[i][j];
int mini = Integer.MAX_VALUE;
// Partition the matrices between i and j
for (int k = i; k <= j - 1; k++) {
/* Compute the cost of multiplying
matrices from i to k and from k+1 to j*/
int ans = func(arr, i, k, dp) + func(arr, k + 1, j, dp) + arr[i - 1] * arr[k] * arr[j];
// Update the minimum cost
mini = Math.min(mini, ans);
}
// Store and return the minimum cost found
dp[i][j] = mini;
return mini;
}
/* Function to set up the parameters
and call the recursive function*/
public int matrixMultiplication(int[] nums) {
int N = nums.length;
// Starting index of the matrix chain
int i = 1;
// Ending index of the matrix chain
int j = N - 1;
int[][] dp = new int[N][N];
for (int[] row : dp)
Arrays.fill(row, -1);
// Call the recursive function
return func(nums, i, j, dp);
}
public static void main(String[] args) {
int[] arr = {10, 20, 30, 40, 50};
// Create an instance of Solution class
Solution sol = new Solution();
// Print the result
System.out.println("The minimum number of operations is " + sol.matrixMultiplication(arr));
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
import sys
class Solution:
def __init__(self):
self.dp = None
""" Recursive function to compute the
minimum cost of matrix multiplication"""
def func(self, arr, i, j):
""" Base case: When there is only one
matrix, no multiplication is needed"""
if i == j:
return 0
# Check if the subproblem is already calculated
if self.dp[i][j] != -1:
return self.dp[i][j]
mini = float('inf')
# Partition the matrices between i and j
for k in range(i, j):
""" Compute the cost of multiplying
matrices from i to k and from k+1 to j"""
ans = self.func(arr, i, k) + self.func(arr, k + 1, j) + arr[i - 1] * arr[k] * arr[j]
# Update the minimum cost
mini = min(mini, ans)
# Store and return the minimum cost found
self.dp[i][j] = mini
return mini
""" Function to set up the parameters
and call the recursive function"""
def matrixMultiplication(self, arr):
N = len(arr)
# Starting index of the matrix chain
i = 1
# Ending index of the matrix chain
j = N - 1
self.dp = [[-1] * N for _ in range(N)]
# Call the recursive function
return self.func(arr, i, j)
if __name__ == "__main__":
arr = [10, 20, 30, 40, 50]
# Create an instance of Solution class
sol = Solution()
# Print the result
print("The minimum number of operations is", sol.matrixMultiplication(arr))
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758
class Solution {
constructor() {
this.dp = null;
}
/* Recursive function to compute the
minimum cost of matrix multiplication*/
func(arr, i, j) {
/* Base case: When there is only one
matrix, no multiplication is needed*/
if (i === j) return 0;
// Check if the subproblem is already calculated
if (this.dp[i][j] !== -1) return this.dp[i][j];
let mini = Infinity;
// Partition the matrices between i and j
for (let k = i; k <= j - 1; k++) {
/* Compute the cost of multiplying
matrices from i to k and from k+1 to j*/
const ans = this.func(arr, i, k) + this.func(arr, k + 1, j) + arr[i - 1] * arr[k] * arr[j];
// Update the minimum cost
mini = Math.min(mini, ans);
}
// Store and return the minimum cost found
this.dp[i][j] = mini;
return mini;
}
/* Function to set up the parameters
and call the recursive function*/
matrixMultiplication(nums) {
const N = nums.length;
// Starting index of the matrix chain
const i = 1;
// Ending index of the matrix chain
const j = N - 1;
this.dp = Array.from({ length: N }, () => Array(N).fill(-1));
// Call the recursive function
return this.func(nums, i, j);
}
}
const arr = [10, 20, 30, 40, 50];
// Create an instance of Solution class
const sol = new Solution();
// Print the result
console.log(`The minimum number of operations is ${sol.matrixMultiplication(arr)}`);