Sudoko Solver

Recursion FAQs (Hard) Hard

The concept behind solving Sudoku puzzles programmatically is often used in the real world as a common example of constraint satisfaction problems (CSPs)
CSPs are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or restrictions
CSPs are applied in areas like AI planning and scheduling, routing problems, and even efficiently allocating resources in large data centers
For instance, Google uses CSPs in their Or-Tools software to solve complex planning and resource allocation problems

Create a program that fills in the blank cells in a Sudoku puzzle to solve it.

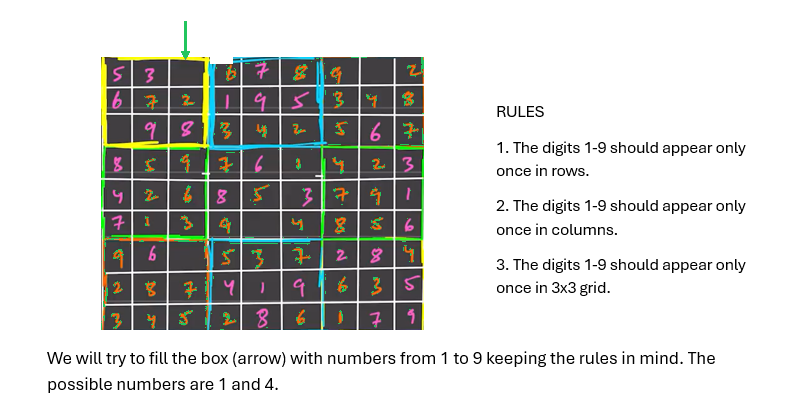
Every sudoku solution needs to follow to these guidelines:

1) In every row, the numbers 1 through 9 must appear exactly once.

2) In every column, the numbers 1 through 9 must appear exactly once.

3) In each of the grid's nine 3x3 sub-boxes, the numbers 1 through 9 must appear exactly once.

Empty cells are indicated by the '.' character.

Constraints

board.length = 9
board[i].length = 9
board[i][j] is a digit or '.'
It is guaranteed that input board has only one solution.

Hints

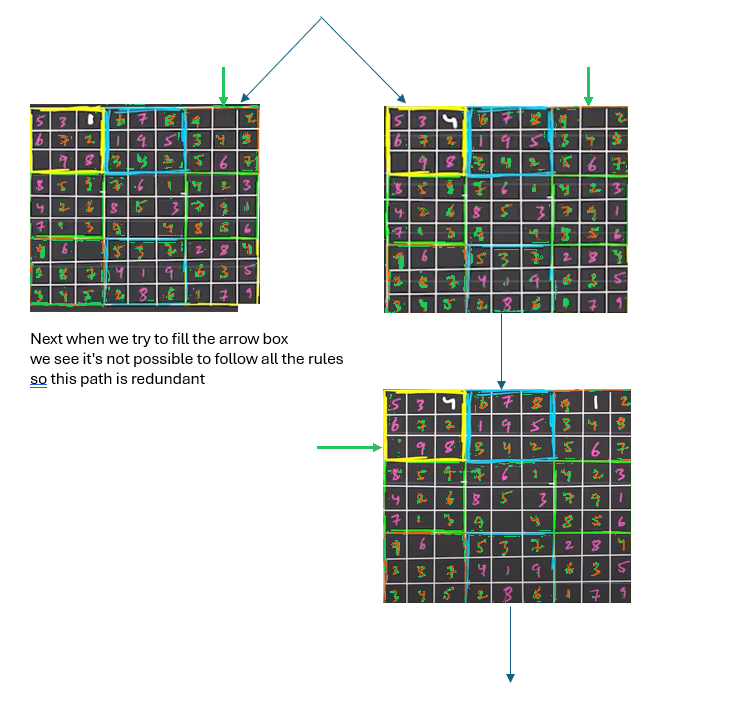
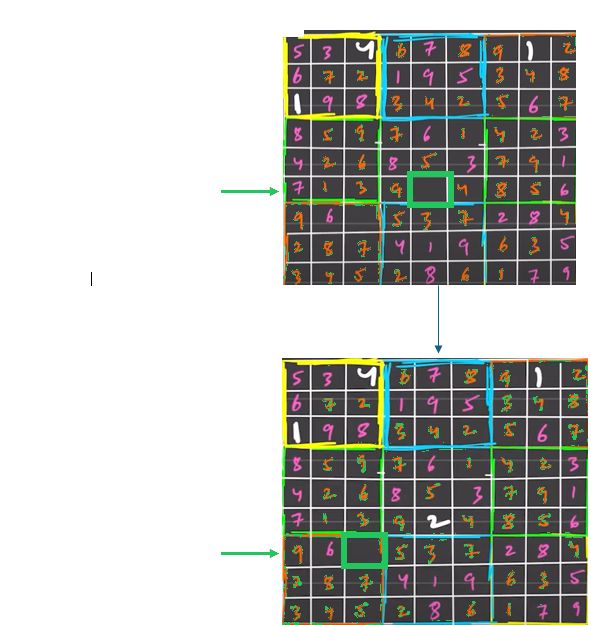
Use recursion to try filling in each empty cell. For each empty cell, try placing numbers 1 through 9. After placing a number, recursively attempt to solve the rest of the puzzle.
Maintain data structures (e.g., sets or arrays) to track used numbers for each row, column, and sub-grid. This avoids repeatedly iterating over the grid to check constraints. Terminate as soon as the puzzle is solved, as only one solution exists for a valid Sudoku.

Company Tags

Airbnb Visa McKinsey & Company ARM Stripe Bungie Alibaba Ernst & Young Flipkart Etsy Medtronic Zoho Zomato Broadcom Riot Games Goldman Sachs Uber Zynga Databricks Activision Blizzard Freshworks Optum Micron Technology Ubisoft Texas Instruments Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Solving Sudoku with Recursion

To solve a Sudoku puzzle in real life, imagine the task as filling in a partially completed grid so that every row, column, and 3x3 sub-box contains the digits from 1 to 9 exactly once. This involves trial and error, checking for conflicts with existing digits, and backtracking when a conflict arises. Think of it as trying to fit pieces into a jigsaw puzzle, where each piece (digit) must fit perfectly without violating any rules.

Intuition

Solving this question can be likened to fitting pieces into a jigsaw puzzle where each piece must fit perfectly without violating any rules. In real life, this means filling in the partially completed grid so that every row, column, and 3x3 sub-box contains the digits from 1 to 9 exactly once. This is done through trial and error: identifying empty cells, attempting to place digits, and checking for conflicts. When a conflict arises, backtrack and try a different digit. This process is naturally recursive, as solving the grid involves solving smaller sub-problems (filling in each cell) that depend on previous placements. By treating each empty cell as a sub-problem and recursively attempting to solve the entire grid, the puzzle can be systematically and efficiently solved.

Approach

Traverse the grid to find the first empty cell. For the empty cell, try placing digits from '1' to '9' one by one.
For each digit, check if it is valid according to Sudoku rules (i.e., it doesn't conflict with any digit in the same row, column, or 3x3 sub-box). If a digit is valid, place it in the cell.
Recursively attempt to solve the rest of the grid with the current digit placed. If placing the current digit doesn't lead to a solution, reset the cell and try the next digit.
Repeat the process until the entire grid is correctly filled, or determine that the puzzle is unsolvable.

<!---<h3> Dry Run

---!>

Solution

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        solve(board);
    }

private:
    // Recursive method to solve the Sudoku
    bool solve(vector<vector<char>>& board) {
        // Size of the board
        int n = 9;  
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                // Empty cell found
                if (board[i][j] == '.') {  
                    for (char digit = '1'; digit <= '9'; digit++) {
                        // Check if digit can be placed
                        if (areRulesMet(board, i, j, digit)) {  
                            // Place digit
                            board[i][j] = digit;  
                            // Recur to place next digits
                            if (solve(board)) {  
                                return true;
                            } else {
                                // Reset if placing digit doesn't solve Sudoku
                                board[i][j] = '.';  
                            }
                        }
                    }
                    // If no digit can be placed, return false
                    return false;  
                }
            }
        }
        return true;  // Sudoku solved
    }

    // Method to check if placing a digit follows Sudoku rules
    bool areRulesMet(vector<vector<char>>& board, int row, int col, char digit) {
        for (int i = 0; i < 9; i++) {
            if (board[row][i] == digit || board[i][col] == digit) {
                // Digit already in row or column
                return false;  
            }
        }
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++) {
            for (int j = startCol; j < startCol + 3; j++) {
                if (board[i][j] == digit) {
                    // Digit already in 3x3 sub-box
                    return false;  
                }
            }
        }
        // Digit can be placed
        return true;  
    }
};

int main() {
    Solution solution;
    vector<vector<char>> board = {
        {'5', '3', '.', '.', '7', '.', '.', '.', '.'},
        {'6', '.', '.', '1', '9', '5', '.', '.', '.'},
        {'.', '9', '8', '.', '.', '.', '.', '6', '.'},
        {'8', '.', '.', '.', '6', '.', '.', '.', '3'},
        {'4', '.', '.', '8', '.', '3', '.', '.', '1'},
        {'7', '.', '.', '.', '2', '.', '.', '.', '6'},
        {'.', '6', '.', '.', '.', '.', '2', '8', '.'},
        {'.', '.', '.', '4', '1', '9', '.', '.', '5'},
        {'.', '.', '.', '.', '8', '.', '.', '7', '9'}
    };
    solution.solveSudoku(board);
    for (const auto& row : board) {
        for (char c : row) {
            cout << c << " ";
        }
        cout << endl;
    }
    return 0;
}
class Solution {
    public void solveSudoku(char[][] board) {
        solve(board);
    }

    // Recursive method to solve the Sudoku
    private boolean solve(char[][] board) {
        int n = 9;  // Size of the board
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                // Empty cell found
                if (board[i][j] == '.') {  
                    for (char digit = '1'; digit <= '9'; digit++) {
                        // Check if digit can be placed
                        if (areRulesMet(board, i, j, digit)) {  
                            // Place digit
                            board[i][j] = digit;  
                            // Recur to place next digits
                            if (solve(board)) {  
                                return true;
                            } else {
                                // Reset if placing digit doesn't solve Sudoku
                                board[i][j] = '.';  
                            }
                        }
                    }
                    // If no digit can be placed, return false
                    return false;  
                }
            }
        }
        // Sudoku solved
        return true;  
    }

    // Method to check if placing a digit follows Sudoku rules
    private boolean areRulesMet(char[][] board, int row, int col, char digit) {
        for (int i = 0; i < 9; i++) {
            if (board[row][i] == digit || board[i][col] == digit) {
                // Digit already in row or column
                return false;  
            }
        }
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++) {
            for (int j = startCol; j < startCol + 3; j++) {
                if (board[i][j] == digit) {
                    // Digit already in 3x3 sub-box
                    return false;  
                }
            }
        }
        // Digit can be placed
        return true;  
    }

    // Main method for testing
    public static void main(String[] args) {
        Solution solution = new Solution();
        char[][] board = {
            {'5', '3', '.', '.', '7', '.', '.', '.', '.'},
            {'6', '.', '.', '1', '9', '5', '.', '.', '.'},
            {'.', '9', '8', '.', '.', '.', '.', '6', '.'},
            {'8', '.', '.', '.', '6', '.', '.', '.', '3'},
            {'4', '.', '.', '8', '.', '3', '.', '.', '1'},
            {'7', '.', '.', '.', '2', '.', '.', '.', '6'},
            {'.', '6', '.', '.', '.', '.', '2', '8', '.'},
            {'.', '.', '.', '4', '1', '9', '.', '.', '5'},
            {'.', '.', '.', '.', '8', '.', '.', '7', '9'}
        };
        solution.solveSudoku(board);
        for (char[] row : board) {
            for (char c : row) {
                System.out.print(c + " ");
            }
            System.out.println();
        }
    }
}
class Solution:
    def solveSudoku(self, board):
        self.solve(board)

    # Recursive method to solve the Sudoku
    def solve(self, board):
        # Size of the board
        n = 9  
        for i in range(n):
            for j in range(n):
                # Empty cell found
                if board[i][j] == '.':  
                    for digit in '123456789':
                        # Check if digit can be placed
                        if self.are_rules_met(board, i, j, digit):  
                             # Place digit
                            board[i][j] = digit 
                            # Recur to place next digits
                            if self.solve(board):  
                                return True
                            else:
                                # Reset if placing digit doesn't solve Sudoku
                                board[i][j] = '.'
                    # If no digit can be placed, return False              
                    return False  
        # Sudoku solved            
        return True  

    # Method to check if placing a digit follows Sudoku rules
    def are_rules_met(self, board, row, col, digit):
        for i in range(9):
            if board[row][i] == digit or board[i][col] == digit:
                # Digit already in row or column
                return False  
        start_row, start_col = 3 * (row // 3), 3 * (col // 3)
        for i in range(start_row, start_row + 3):
            for j in range(start_col, start_col + 3):
                if board[i][j] == digit:
                     # Digit already in 3x3 sub-box
                    return False 
         # Digit can be placed            
        return True 


if __name__ == "__main__":
    solution = Solution()
    board = [
        ['5', '3', '.', '.', '7', '.', '.', '.', '.'],
        ['6', '.', '.', '1', '9', '5', '.', '.', '.'],
        ['.', '9', '8', '.', '.', '.', '.', '6', '.'],
        ['8', '.', '.', '.', '6', '.', '.', '.', '3'],
        ['4', '.', '.', '8', '.', '3', '.', '.', '1'],
        ['7', '.', '.', '.', '2', '.', '.', '.', '6'],
        ['.', '6', '.', '.', '.', '.', '2', '8', '.'],
        ['.', '.', '.', '4', '1', '9', '.', '.', '5'],
        ['.', '.', '.', '.', '8', '.', '.', '7', '9']
    ]
    solution.solveSudoku(board)
    for row in board:
        print(" ".join(row))
class Solution {
    solveSudoku(board) {
        this.solve(board);
    }

    // Recursive method to solve the Sudoku
    solve(board) {
        const n = 9;
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < n; j++) {
                // Empty cell found
                if (board[i][j] === '.') {
                    for (let digit = '1'; digit <= '9'; digit++) {
                        // Check if digit can be placed
                        if (this.areRulesMet(board, i, j, digit)) {
                            // Place digit
                            board[i][j] = digit;
                            if (this.solve(board)) {
                                // Recur to place next digits
                                return true;
                            } else {
                                // Reset if placing digit doesn't solve Sudoku
                                board[i][j] = '.';
                            }
                        }
                    }
                    // If no digit can be placed, return false
                    return false;
                }
            }
        }
        // Sudoku solved
        return true;
    }

    // Method to check if placing a digit follows Sudoku rules
    areRulesMet(board, row, col, digit) {
        for (let i = 0; i < 9; i++) {
            if (board[row][i] === digit || board[i][col] === digit) {
                // Digit already in row or column
                return false;
            }
        }
        const startRow = Math.floor(row / 3) * 3;
        const startCol = Math.floor(col / 3) * 3;
        for (let i = startRow; i < startRow + 3; i++) {
            for (let j = startCol; j < startCol + 3; j++) {
                if (board[i][j] === digit) {
                    // Digit already in 3x3 sub-box
                    return false;
                }
            }
        }
        // Digit can be placed
        return true;
    }
}

// Example usage
const board = [
    ['5', '3', '.', '.', '7', '.', '.', '.', '.'],
    ['6', '.', '.', '1', '9', '5', '.', '.', '.'],
    ['.', '9', '8', '.', '.', '.', '.', '6', '.'],
    ['8', '.', '.', '.', '6', '.', '.', '.', '3'],
    ['4', '.', '.', '8', '.', '3', '.', '.', '1'],
    ['7', '.', '.', '.', '2', '.', '.', '.', '6'],
    ['.', '6', '.', '.', '.', '.', '2', '8', '.'],
    ['.', '.', '.', '4', '1', '9', '.', '.', '5'],
    ['.', '.', '.', '.', '8', '.', '.', '7', '9']
];

const solution = new Solution();
solution.solveSudoku(board);
console.log(board.map(row => row.join(' ')).join('\n'));

Complexity Analysis

Time Complexity : O(9^(N*N)), as each cell can be filled with 1 to 9 digits and there are n*n cells.

Space Complexity O(n), where n is the depth of the recursion stack.

Code

Problem List