Floor and Ceil in Sorted Array

Binary Search Logic Building Easy Go Ad-Free - ₹20/mo

Given a sorted array nums and an integer x. Find the floor and ceil of x in nums. The floor of x is the largest element in the array which is smaller than or equal to x. The ceiling of x is the smallest element in the array greater than or equal to x. If no floor or ceil exists, output -1.

Examples:

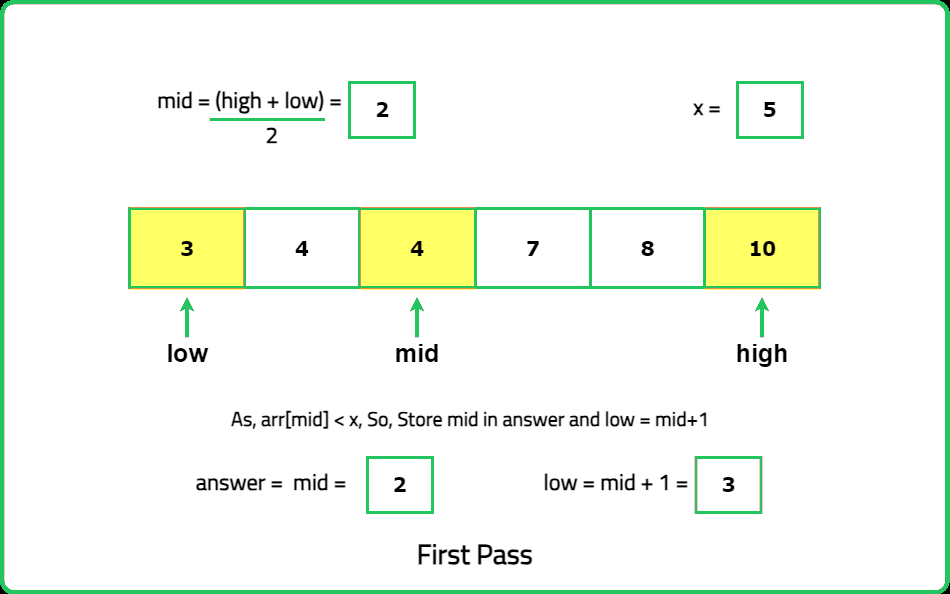
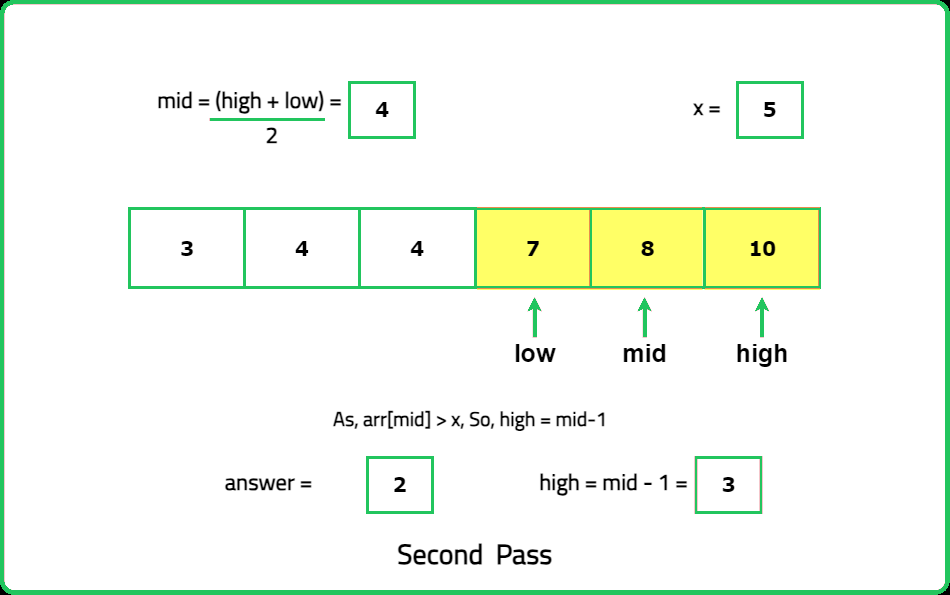
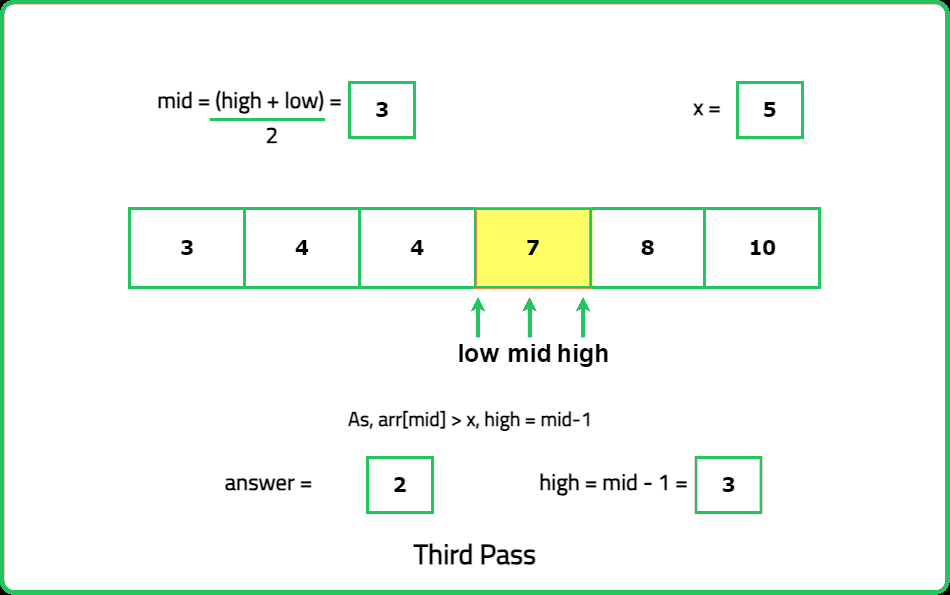
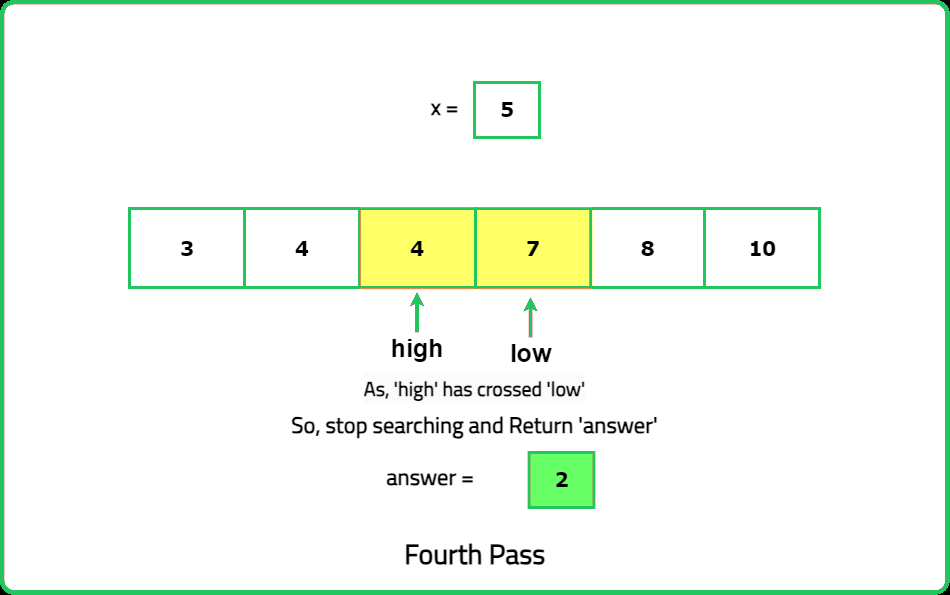
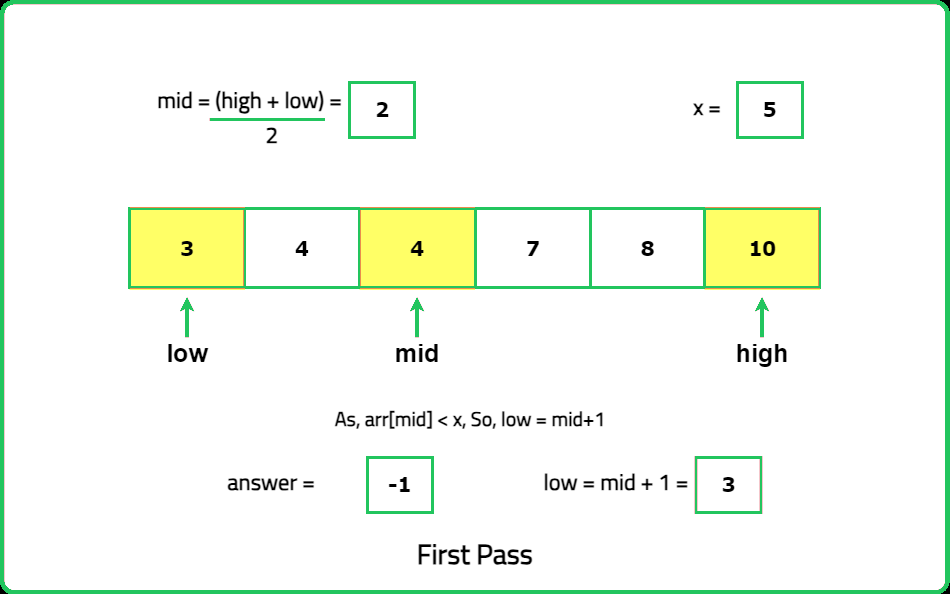
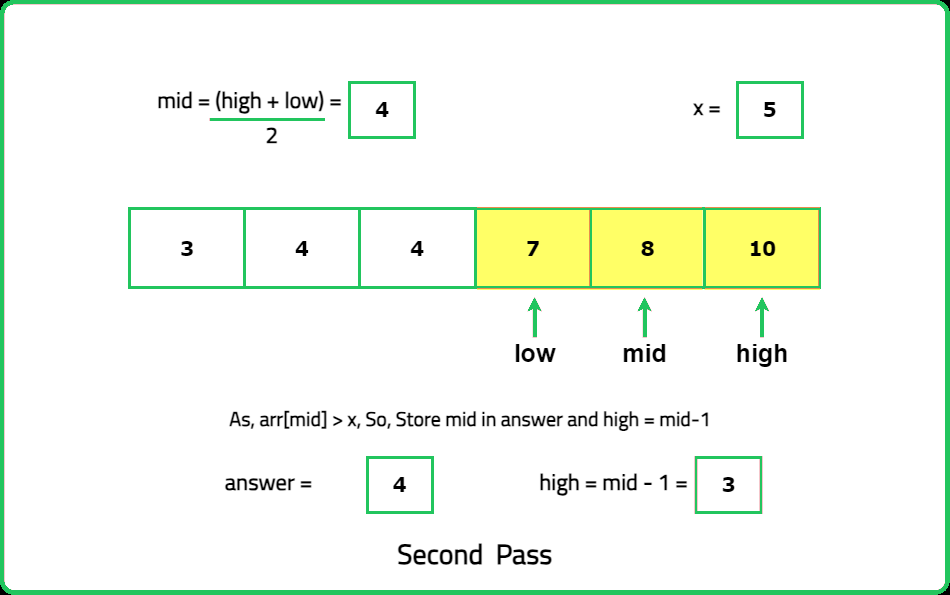
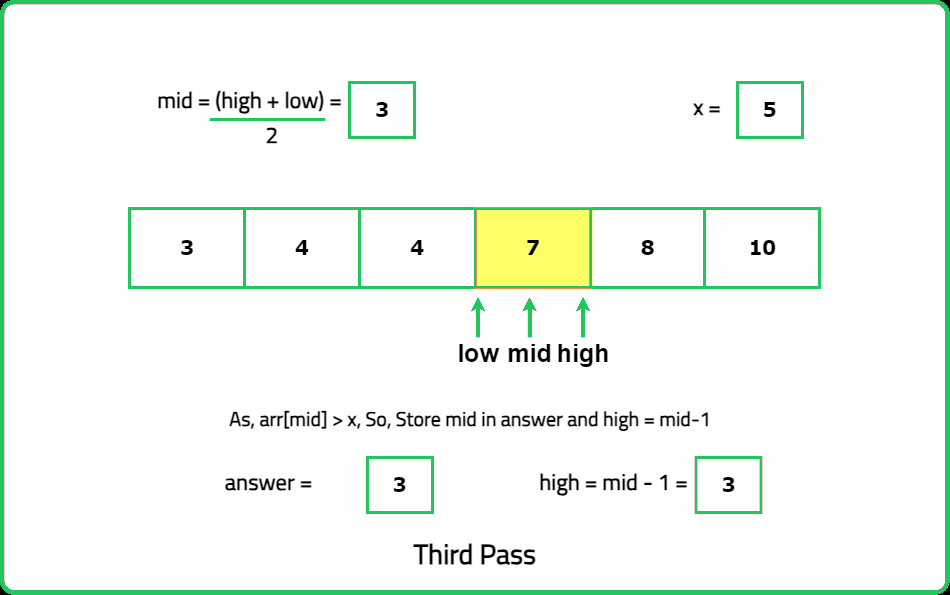
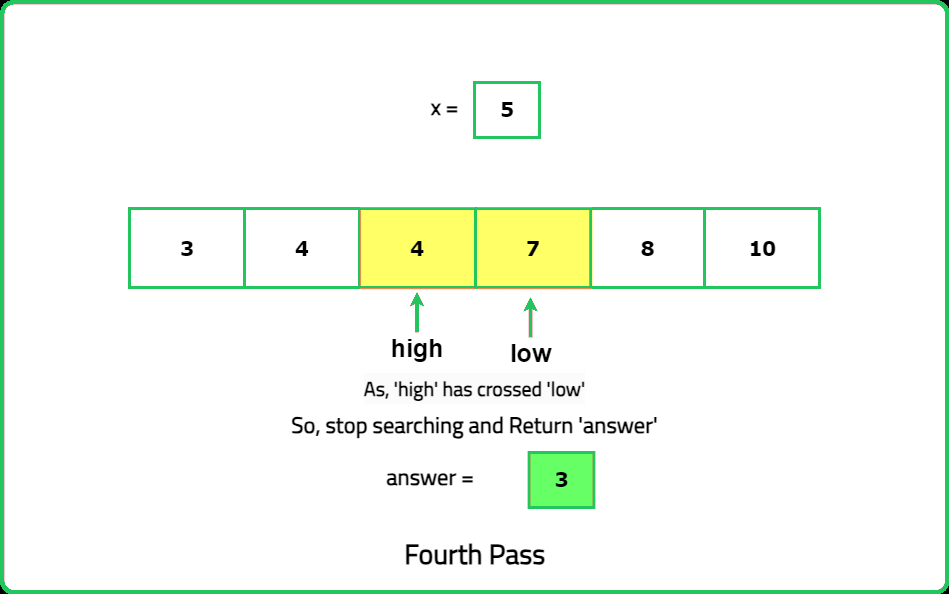
Input : nums =[3, 4, 4, 7, 8, 10], x= 5

Output: 4 7

Explanation: The floor of 5 in the array is 4, and the ceiling of 5 in the array is 7.

Input : nums =[3, 4, 4, 7, 8, 10], x= 8

Output: 8 8

Explanation: The floor of 8 in the array is 8, and the ceiling of 8 in the array is also 8.

Input : nums = [8, 4, 12, 2, 6, 10, 14], x= 1

Constraints

1 <= nums.length <= 10⁵
0 < nums[i], x < 10⁵
nums is sorted in ascending order.

Hints

"Perform a binary search for x in the sorted array. During the search: If nums[mid]≤x, update the floor to nums[mid] and move right. If nums[mid]≥x, update the ceiling to nums[mid] and move left."
If x is smaller than the smallest element, the floor is −1. If x is larger than the largest element, the ceiling is −1.

Company Tags

Etsy Lyft Red Hat GE Healthcare KPMG McKinsey & Company Twilio Chewy Mastercard American Express Cloudflare Nutanix Wayfair Ubisoft Johnson & Johnson PwC Uber Snowflake Target Ernst & Young PayPal Roblox Zomato Instacart HashiCorp TCS Cognizant Accenture Infosys Capgemini Wipro

Editorial

Brute Force Approach

Intuition

Given have a sorted array where each element is distinct requirement is to find two specific values related to 𝑥 its floor (largest element ≤ x) and its ceiling (smallest element ≥ x). Brute force involves a straightforward approach where we iterate through the entire array to find the required values. This method ensures that we consider each element individually to determine if it meets the criteria for being the floor or ceiling of x.

Approach

Initialize variables to store the floor and ceiling values. Start them with values that indicate no floor or ceiling found (e.g., -1).
Traverse through each element in the sorted array nums.
Update the floor if the current element is ≤ x and is greater than the current floor value.
Update the ceiling if the current element is ≥ x and is less than the current ceiling value.
After iterating through the array, check if valid floor and ceiling values were found. If either value remains as the initial value (-1), it indicates no valid floor or ceiling exists for x.

Edge Cases

Handle cases where x is smaller than all elements in nums (no floor).

Handle cases where x is larger than all elements in nums (no ceiling).

Consider scenarios where x exactly matches an element in nums, ensuring the element itself is identified as both floor and ceiling.

Complexity Analysis

Time Complexity: O(N) where N is the number of elements in nums. This is because we potentially need to examine each element in the worst case.
Space Complexity: O(1), as we only use a constant amount of additional space regardless of the input size.

Optimal Approach

Intuition

For getting the floor value of x in nums, divide the array in two halves and compare the middle values with x. When x is less than or equal to the middle element, store the middle element as answer and will try to find a larger number that satisfies the same condition.

From the given statements, we can understand that the ceiling value of x, is basically the lower bound of x.

Approach

Find floor

Use two pointers, low and high initialized with the first and last indexes which will makr our search space. Use an answer variable initialized with -1 to store the floor value.
Calculate the middle element, and compare its value as described below :

When the middle element is less than or equal to the given element, store it as a possible answer and eliminate the left half to look for a greater element in the right part of the array.
In case the middle element is greater than the given element, eliminate the right half and reduce the search space to left half to look for a smaller element.
Repeat these steps until the low pointer lesser than or equal to the high pointer.

Find ceil

For calculating the ceil value, follow a similar approach, but compare the values depending upon the below points:

In this case, store the middle element as a possible answer when the middle elements value is greater than or equal to the given element. Eliminate the right half to look for a smaller element in the left half which satisfies the same condition.
When the middle element is smaller than the given element, eliminate the left half to search for a larger element in the right half of the given array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Helper function to find the floor of x
    int findFloor(vector<int>& nums, int n, int x) {
        int low = 0, high = n - 1;
        int ans = -1;

        // Perform binary search to find floor value
        while (low <= high) {
            int mid = (low + high) / 2;
            
            /*Check if mid element lesser than 
			      or equal to x, if it is update ans 
		        and eliminate the left half */
            if (nums[mid] <= x) {
                ans = nums[mid];
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return ans;
    }

    // Helper function to find the ceil of x
    int findCeil(vector<int>& nums, int n, int x) {
        int low = 0, high = n - 1;
        int ans = -1;

        // Perform binary search to find ceil value
        while (low <= high) {
            int mid = (low + high) / 2;
            
             /*Check if mid element greater than 
			      or equal to x, if it is update ans 
		        and eliminate the left half */
            if (nums[mid] >= x) {
                ans = nums[mid];
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }

        return ans;
    }

public:
    // Function to find both floor and ceil of x in nums
    vector<int> getFloorAndCeil(vector<int> nums, int x) {
        int n = nums.size();
        int floor = findFloor(nums, n, x);
        int ceil = findCeil(nums, n, x);
        return {floor, ceil};
    }
};

int main() {
    vector<int> nums = {3, 4, 4, 7, 8, 10};
    int x = 5;

    // Create an instance of the Solution class
    Solution sol;

    vector<int> result = sol.getFloorAndCeil(nums, x);

    cout << "The floor and ceil are: " << result[0] << " " << result[1] << endl;

    return 0;
}
import java.util.*;

class Solution {
    private int findFloor(int[] nums, int n, int x) {
        int low = 0, high = n - 1;

        // Stores the floor value
        int ans = -1;

        // Perform binary search to find the floor value
        while (low <= high) {
            int mid = (low + high) / 2;

             /*Check if mid element lesser than 
			      or equal to x, if it is update ans 
		        and eliminate the left half */
            if (nums[mid] <= x) {
                ans = nums[mid];
                low = mid + 1;
            }
            /*If mid element greater than x, 
            then eliminate the right half */
            else {
                high = mid - 1;
            }
        }
        return ans;
    }

    private int findCeil(int[] nums, int n, int x) {
        int low = 0, high = n - 1;
        int ans = -1;

        // Perform binary search to find ceil value
        while (low <= high) {
            int mid = (low + high) / 2;

            /*Check if mid element greater than 
			      or equal to x, if it is update ans 
		        and eliminate the left half */
            if (nums[mid] >= x) {
                ans = nums[mid];
                high = mid - 1;
            }
            /*If mid element lesser than x, 
            then eliminate the left half */
            else {
                low = mid + 1;
            }
        }
        return ans;
    }

    // Function to find both floor and ceil of x 
    public int[] getFloorAndCeil(int[] nums, int x) {
        int n = nums.length;

        /*Function call to find the floor 
        value using helper functions*/
        int floor = findFloor(nums, n, x);

        /* Function call to find the ceil 
        value using helper functions*/
        int ceil = findCeil(nums, n, x);

        return new int[] {floor,ceil};
    }

    public static void main(String[] args) {
        int[] nums = {3, 4, 4, 7, 8, 10};
        int x = 5;

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Function call to get floor and ceil
        int[] result = sol.getFloorAndCeil(nums, x);

        System.out.println("The floor and ceil are: " + result[0] + " " + result[1]);
    }
}
class Solution:
    def findFloor(self, nums, n, x):
        low, high = 0, n - 1
        ans = -1

        # Perform binary search to find the floor value
        while low <= high:
            mid = (low + high) // 2

            """Check if mid element lesser than 
			      or equal to x, if it is update ans 
		        and eliminate the left half """
            if nums[mid] <= x:
                ans = nums[mid]
                low = mid + 1
            else:
                high = mid - 1
        return ans

    def findCeil(self, nums, n, x):
        low, high = 0, n - 1
        ans = -1

        # Perform binary search to find the ceil value
        while low <= high:
            mid = (low + high) // 2

            """Check if mid element greater than 
			      or equal to x, if it is update ans 
		        and eliminate the left half """
            if nums[mid] >= x:
                ans = nums[mid]
                high = mid - 1
            else:
                low = mid + 1
        return ans

    # Function to find both floor and ceil of x 
    def getFloorAndCeil(self, nums, x):
        n = len(nums)

        """ Function call to find the floor 
		    value using helper functions"""
        floor = self.findFloor(nums, n, x)

        """ Function call to find the ceil 
		    value using helper functions"""
        ceil = self.findCeil(nums, n, x)

        return [floor, ceil]

if __name__ == "__main__":
    nums = [3, 4, 4, 7, 8, 10]
    x = 5

    # Create an instance of the Solution class
    sol = Solution()

    # Function call to get floor and ceil
    result = sol.getFloorAndCeil(nums, x)

    print("The floor and ceil are:", result[0], result[1])
class Solution {
    // Helper function to find the floor of x
    findFloor(nums, n, x) {
        let low = 0, high = n - 1;
        let ans = -1;

        // Perform binary search to find the floor value
        while (low <= high) {
            let mid = Math.floor((low + high) / 2);

            /*Check if mid element lesser than 
			      or equal to x, if it is update ans 
		        and eliminate the left half */
            if (nums[mid] <= x) {
                ans = nums[mid];  
                low = mid + 1;    
            } 
            else {
                high = mid - 1;
            }
        }
        return ans; 
    }

    // Helper function to find the ceil of x
    findCeil(nums, n, x) {
        let low = 0, high = n - 1;
        let ans = -1;

        //Perform binary search to find the ceil value
        while (low <= high) {
            let mid = Math.floor((low + high) / 2);

            /*Check if mid element greater than 
			      or equal to x, if it is update ans 
		        and eliminate the left half */
            if (nums[mid] >= x) {
                ans = nums[mid];  
                high = mid - 1;  
            }
            else {
                low = mid + 1;
            }
        }
        return ans;  
    }

    // Function to find both floor and ceil of x 
        getFloorAndCeil(nums, x) {
        let n = nums.length;  

        /* Function call to find the floor 
		    value using helper functions*/
        let floor = this.findFloor(nums, n, x);

        /* Function call to find the ceil 
		    value using helper functions*/
        let ceil = this.findCeil(nums, n, x);

        return [floor, ceil]; 
    }
}

let nums = [3, 4, 4, 7, 8, 10];
let x = 5;

// Create an instance of the Solution class
let sol = new Solution();

// Function call to get floor and ceil
let result = sol.getFloorAndCeil(nums, x);

console.log("The floor and ceil are:", result[0], result[1]);

Complexity Analysis:

Time Complexity: O(logN), where N is the size of the given array. We are using the Binary Search algorithm, which divides the search space in half each time, resulting in a logarithmic time complexity.

Space Complexity: O(1), as we are not using any extra space to solve this problem.

Frequently Occurring Doubts

Q: How does binary search naturally find the floor and ceiling?

A: Binary search systematically narrows the range: For the floor, you look for the largest element less than or equal to x. For the ceiling, you look for the smallest element greater than or equal to x.

Interview Followup Questions

Q: What if the array is rotated?

A: Identify the pivot point first. Then: Search for the floor and ceiling in the left and right sorted halves separately.

Q: How would you extend this to find all elements between the floor and ceiling?

A: Once the floor and ceiling are identified, use binary search to find the range of indices between them.

Notes

Your notes are automatically saved in your browser's local storage and will persist across sessions on this device.

Problem Categories

Floor and Ceil in Sorted Array

Examples:

Constraints

Hints

Company Tags

Editorial

Brute Force Approach

Intuition

Approach

Edge Cases

Complexity Analysis

Optimal Approach

Intuition

Approach

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code