Search in rotated sorted array-I
Binary Search
Logic Building
Easy
Given an integer array nums, sorted in ascending order (with distinct values) and a target value k. The array is rotated at some pivot point that is unknown. Find the index at which k is present and if k is not present return -1.
Examples:
Input : nums = [4, 5, 6, 7, 0, 1, 2], k = 0
Output: 4
Explanation: Here, the target is 0. We can see that 0 is present in the given rotated sorted array, nums. Thus, we get output as 4, which is the index at which 0 is present in the array.
Input: nums = [4, 5, 6, 7, 0, 1, 2], k = 3
Output: -1
Explanation: Here, the target is 3. Since 3 is not present in the given rotated sorted array. Thus, we get the output as -1.
Input: nums = [4, 5, 6, 7, 0, 1, 2], k = 5
Constraints
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- All values of nums are unique.
- nums is an ascending array that is possibly rotated.
- -104 <= k <= 104
Hints
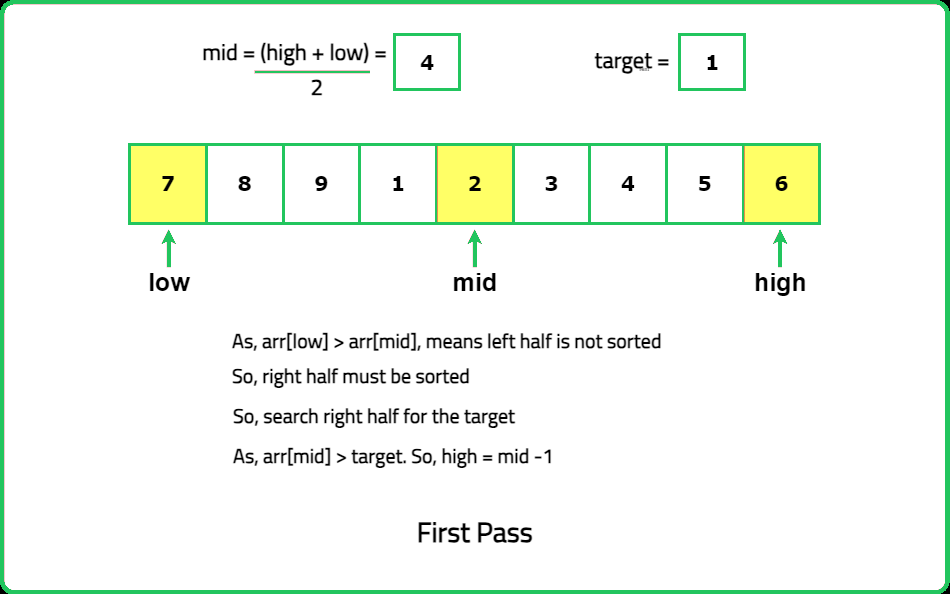
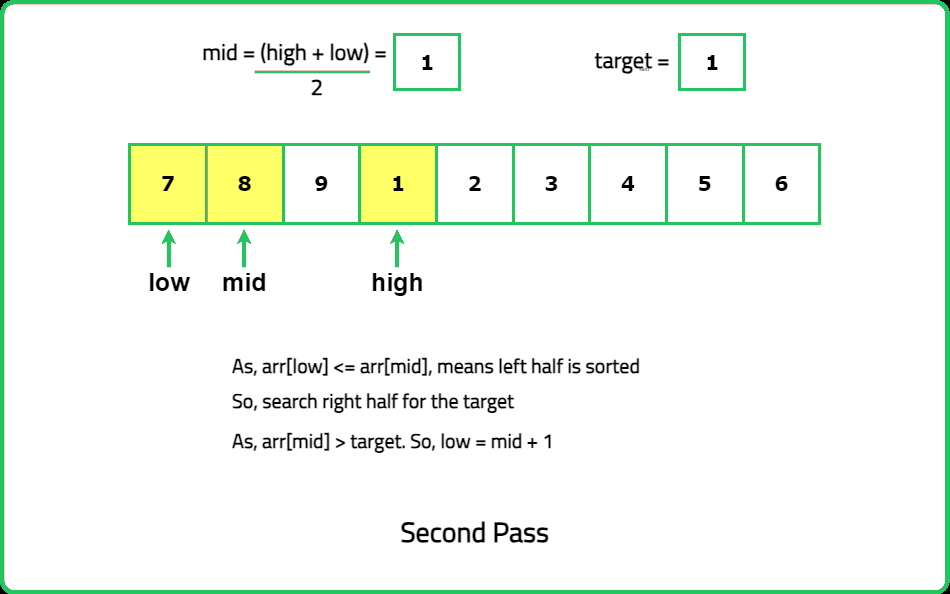
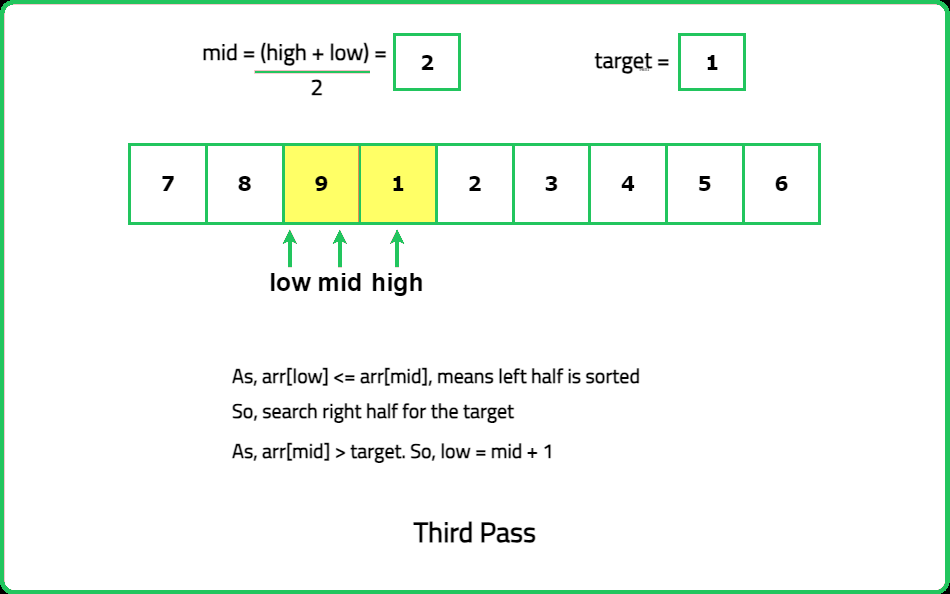
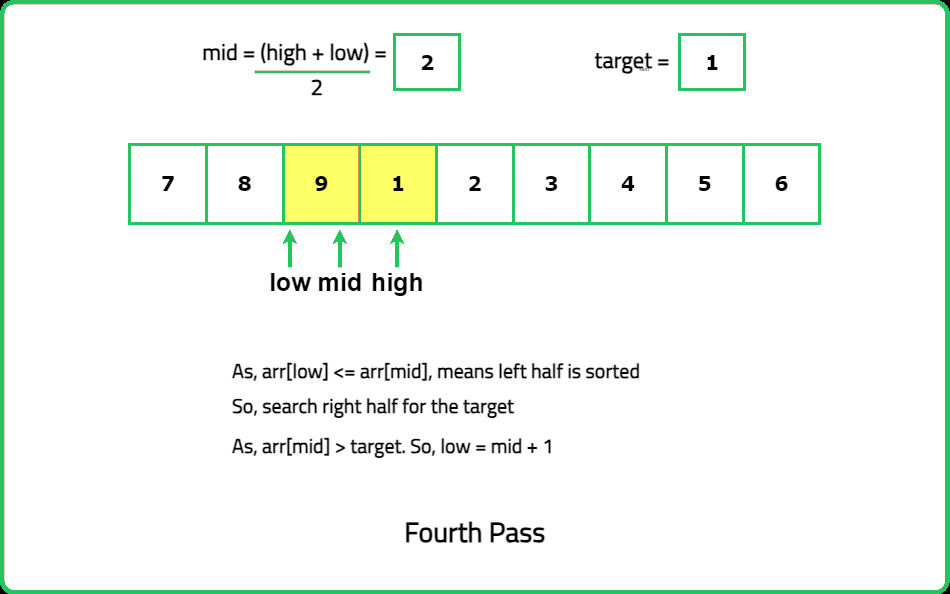
- Use binary search to locate the target value while considering the rotation. During each iteration, check if the target lies in the sorted half of the array.
- "Compare the mid element with the first and last elements to determine which half is sorted: If nums[mid] >= nums[low], the left half is sorted. If nums[mid] <= nums[high], the right half is sorted."
Company Tags
Deloitte
Square
Reddit
Roblox
MongoDB
Zynga
Teladoc Health
Ernst & Young
Nutanix
GE Healthcare
Western Digital
Medtronic
ARM
Snowflake
Cloudflare
Qualcomm
McKinsey & Company
IBM
Twilio
Chewy
Lyft
Seagate Technology
NVIDIA
Epic Games
Walmart
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro